26 Числа Рейнольдса, Фруда, Эйлера, Вебера
Совокупность параметров, определяющих какой-либо гидродинамический процесс, можно рассматривать как конкретное решение дифференциальных уравнений этого процесса. Ему соответствуют вполне определённые начальные и граничные условия. Они представляют собой зависимости или константы, определяющие физические параметры в начальный момент и на границах во время движения. Следовательно, не только уравнения процесса, но также безразмерные формы начальных и граничных условий (условий однозначности) в механически подобных потоках должны быть одинаковыми. Имея это в виду, запишем уравнения Навье-Стокса и приведём их к безразмерному виду, для чего выберем характерные физические параметры L, V, T, P, F0 (если F - cила тяжести, то в качестве F0 удобно взять ускорение g свободного падения) и отнесём к ним соответствующие размерные величины:
Для
плотности и вязкости, которые считаем
постоянными, характерные величины не
выбираем, так как они сами ими являются.
Примем также во внимание размерность
дифференциальных операторов 
и grad:
;
Векторное уравнение Навье-Стокса можно представить в виде
Чтобы
придать этому уравнению безразмерный
вид, разделим все его члены на
коэффициент 
при
конвективном ускорении. Получим
где дифференциальные операции выполняются по безразмерным переменным. В этом уравнение все члены, включая комбинации характерных параметров, безразмерны. Для всех динамических подобных потоков оно должно быть одинаковым, а следовательно, группы потоков были одинаковыми, т.е.
(1.50)
Входящие
в условия (1.50) безразмерные комплексы
играют роль критериев подобия и имеют
следующие собственные наименования: 
-
число Фруда;
-
число Эйлера;
-
число Рейнольдса;
-
число Струхала.
27 Понятие о гидравлических сопротивлениях, виды потерь напора (местные и по длине)
Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину.
Гидравлические потери обычно разделяют на местные потери и потери на трение по длине.
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями (рис 1.18), т.е. местными изменениями формы и размеры русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется её скорость и обычно возникают крупные вихри. Последние образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям.
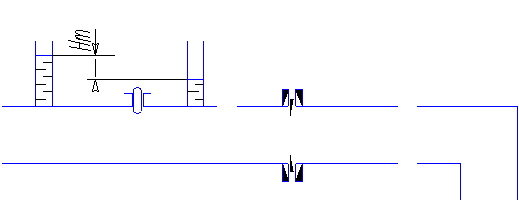
Местные сопротивления напора определяются по формуле следующим образом:
или в единицах давления
Выражение (1.5.4) часто называют формулой Вейсбаха. В ней V - средняя по сечению скорость в трубе, в которой установлено данное местное сопротивление.
Потери на трение по длине - это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Рассматриваемые потери обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах.
Потерю напора на трение можно выразить по общей формуле для гидравлического потерь, т.е.
или
