
- •1.Понятие жидкости. Реальная и идеальная жидкости
- •2. Метод гидравлических исследований
- •3. Силы, действующие на жидкость. Понятие давления
- •4. Основные свойства капельных жидкостей
- •5. Гидростатическое давление и его свойство
- •7. Дифференциальные уравнения равновесия жидкости и их интегрирование для простейшего случая
- •8. Абсолютное и избыточное давление.
- •9 Пьезометрическая высота. Вакуум. Измерение давления
- •10. Основное уравнение гидростатики Потенциальная, удельная энергия жидкости.
- •14 Понятие о движении жидкости как непрерывной деформации сплошной материальной среды
- •15 .Установившееся и неустановившееся течение жидкости
- •19 Уравнение неразрывности
- •22 Геометрическая и энергетическая интерпретация уравнения Бернулли
- •24 Влияние различных факторов на движение жидкости
- •25 Понятие о подобных потоках и критериях подобия
- •26 Числа Рейнольдса, Фруда, Эйлера, Вебера
- •27 Понятие о гидравлических сопротивлениях, виды потерь напора (местные и по длине)
- •28 Общая формула для потерь напора по длине при установившемся равномерном движении жидкости. Коэффициент Дарси
- •29 Основное уравнение равномерного движения
- •30 Касательные напряжения. Обобщённый закон Ньютона
- •31 Ламинарный и турбулентный режимы движения жидкости. Критическое число Рейнольдса
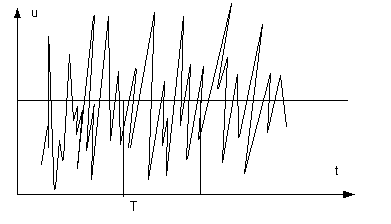
- •32 Пульсации скоростей при турбулентном режиме. Мгновенная и местная осреднённые скорости
- •33 Потери напора по длине при равномерном ламинарном движении жидкости
- •34 Распределение скоростей по живому сечению в цилиндрической трубе при ламинарном режиме. Коэффициент Дарси при ламинарном течении
- •35 Потери напора при равномерном турбулентном движении жидкости
- •36 Механизм турбуллизации потока: процесс перемешивания жидкости, ядро течения и пристенный слой
- •38 Коэффициент Дарси при турбулентном движении жидкости, экспериментальные методы его определения
- •39 График Никурадзе
- •40 Местные сопротивления, основные их виды
- •41. Понятие объемной гидромашины. Насосы, гидродвигатели.
- •46. Основные термины и определения
- •47. Величины, характеризующие рабочий процесс огм: подача (расход), рабочий объем, давление, мощность, коэффициент полезного действия, частота вращения, крутящий момент.
- •48. Классификация, конструктивные схемы и принцип действия огм
- •49. Шестеренные насосы с внешним и внутренним зацеплением
- •50. Винтовые машины. Шиберные (пластинчатые) гидромашины однократного и многократного действия
- •51. Радиально-поршневые гидромашины
- •52. Аксиально-поршневые гидромашины, основные их системы
- •53.Основные понятия и определения, принцип действия. Насосный, аккумуляторный. Магистральный, следящий гидропривод. Замкнутый и разомкнутый гидропривод.
- •54. Гидродроссели и дросселирующие гидрораспределители. Постоянные дроссели . Ламинарные и и турбулентные гидрораспределители. Дроссельные регуляторы.
- •56. Струйный гидрораспределитель. Гидроклапаны. Типы клапанов переливной, предохранительный, редукционный. Течения в них. Расчет гидроклапанов.
- •57. Объемное регулирование скорости выходного звена гидропривода. Дроссельное регулирование скорости выходного звена гидропривода при последовательном и паралелльном включении дросселя.
- •59. Дроссельный способ регулирования огп с установкой дросселя на входе в гидродвигатель, на выходе из гидродвигателя и параллельно гидродвигателю
- •60)Основные параметры привода. Располагаемая и потребная характеристики гидропривода
- •61) Статические характеристики объемного гидропривода с дроссельным регулированием.
- •62) Энергетические характеристики гидропривода.
- •63,64) Методы измерения параметров объемных гидроприводов. Измерение давления, расхода, температуры рабочих сред, частоты вращения и крутящего момента.
7. Дифференциальные уравнения равновесия жидкости и их интегрирование для простейшего случая
X,y,z-сост массовой силы
P=f(x,y,z)- одинак давл исходя из со гидростат давления

Разделим
эти уравнения на массу ![]() параллелепипеда
и перейдем к пределу, устремляя
,
и
., к нулю,
т. е. стягивая параллелепипед к исходной
точкеМ. Тогда
в пределе получим уравнения равновесия
жидкости, отнесенные к точке М:
параллелепипеда
и перейдем к пределу, устремляя
,
и
., к нулю,
т. е. стягивая параллелепипед к исходной
точкеМ. Тогда
в пределе получим уравнения равновесия
жидкости, отнесенные к точке М:
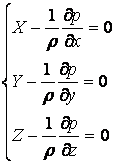
уравнениями Эйлера .
![]()
Трехчлен,
заключенный в скобках, представляет
собой полный дифференциал давления, т.
е. функции ![]() , поэтому
предыдущее уравнение можно переписать
в виде:
, поэтому
предыдущее уравнение можно переписать
в виде:
![]()
или,
![]()
Полученное уравнение выражает приращение давления dp при изменении координат на , и ., в общем случае равновесия жидкости.
Если предположить, что на жидкость действует только сила тяжести, и направить ось z вертикально вверх, то X=Y=O, Z=g и, следовательно, вместо уравнения (2.7) для этого частного случая равновесия жидкости получим
![]()
После интегрирования будем иметь
![]()
Постоянную интегрирования найдем, подставив параметры свободной поверхности, для которой при z = z0 p = р0
Получим
![]() .
.
При этом
![]()
![]()
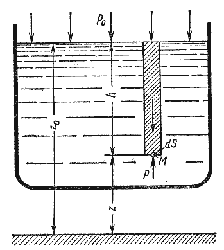
8. Абсолютное и избыточное давление.
Абсолютным называется давление, определённое с учетом атмосферного давления. Превышение абсолютного давления над атмосферным давлением называется избыточным давлением. Т.о. избыточное давление показывает насколько отличается давление в точке измерения от атмосферного.
![]()
 .
.
Таким образом, возможны два случая:
1 Случай: Величина абсолютного давления больше атмосферного давления.
![]() ➨
➨![]()
Такое положительное избыточное давление называют манометрическим.
Манометрическое давление показывает насколько давление в точке измерения больше атмосферного.
2 случай: Величина абсолютного давления меньше атмосферного давления.
![]() ➨
➨
![]()
Такое отрицательное избыточное давление называют вакуумметрическим (величиной вакуума).
Вакуумметрическое давление показывает насколько давление в точке измерения меньше атмосферного.
9 Пьезометрическая высота. Вакуум. Измерение давления

![]() .
.
где ![]() —
абсолютное давление в жидкости на уровне
присоединения пьезометра;
—
абсолютное давление в жидкости на уровне
присоединения пьезометра; ![]() —
атмосферное давление.
—
атмосферное давление.
Отсюда высота подъема жидкости в пьезометре
![]() )
)
где ризб — избыточное давление на уровне присоединения пьезометра.
Часто Давление в жидкостях или газах численно выражают в виде соответствующей этому давлению пьезометрической высоты по формуле (2.9). Если абсолютное давление в жидкости или газе меньше атмосферного, то говорят, что имеет место разрежение, или вакуум. За величину разрежения, или вакуума, принимается недостаток до атмосферного давления:
![]() или
или ![]()
(вакуумметр)
10. Основное уравнение гидростатики Потенциальная, удельная энергия жидкости.
![]()
Сократив все члены уравнения на dS, получим:
![]()
Давление во всех точках свободной поверхности одинаково и равно р0, следовательно, давление во всех точках жидкости на глубине h также одинаково согласно основному уравнения гидростатики. Поверхность, давление на которой одинаково, называется поверхностью уровня. В данном случае поверхности уровня являются горизонтальными плоскостями.
Выберем некоторую горизонтальную плоскость сравнения, проходящую на расстоянии z0 от свободной поверхности, тогда можно записать уравнение гидростатики в виде:
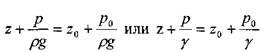
Все члены уравнения имеют линейную размерность и носят название:
- геометричкская высота,
![]() -
пьезометрическая высота
-
пьезометрическая высота
Величина![]() носит
название гидростатического напора.
носит
название гидростатического напора.
12 Сила давления жидкости на плоские и кривые поверхности

Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке :
![]()
где ![]() —
давление на свободной поверхности;
—
давление на свободной поверхности; ![]() —
глубина расположения площадки
.
—
глубина расположения площадки
.
Для
определения полной силы ![]() проинтегрируем
полученное выражение по всей площади
проинтегрируем
полученное выражение по всей площади ![]() :
:
![]()
где ![]() —
координата площадки
.
—
координата площадки
.
Следовательно,
![]()
( здесь
здесь![]() — глубина
расположения центра тяжести площади S. ),
— глубина
расположения центра тяжести площади S. ),
или
![]()
те
полная сила давления жидкости на плоскую
стенку равна произведению площади
стенки на гидростатическое давление ![]() в
центре тяжести этой площади.
в
центре тяжести этой площади.
Кривая поверхность
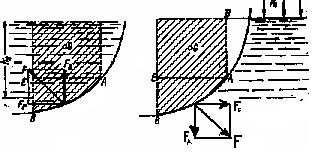
1) жидкость расположена сверху
2) жидкость расположена снизу
В первом случае выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия в вертикальном и горизонтальном направлениях.
Условие равновесия объема ABCD в вертикальном направлении имеет вид
FB = p0SГ + G
где — давление на свободной поверхности жидкости; SГ — площадь горизонтальной проекции поверхности АВ; G — вес выделенного объема жидкости.
Условие равновесия того же объема в горизонтальном направлении запишем
FГ=SBρghC+p0SB
Определив по формулам (1.31) и (1.32) вертикальную и горизонтальную составляющие полной силы давления F, найдем
![]()
