Газовые смеси
В технике в качестве рабочих тел чаще используются не чистые вещества, а смеси различных газов. Под газовой смесью в данном случае понимают механическую смесь чистых веществ, называемых компонентами смеси, не вступающих друг с другом в химические реакции. Примером газовой смеси является воздух, основными компоненты которого являются кислород и азот. Если компонентами смеси являются идеальные газы, то и смесь в целом также будем считать идеальным газом.
При рассмотрении смесей предполагается, что:
- каждый газ, входящий в состав смеси, равномерно распределён по всему объёму, то есть его объём равен объёму всей смеси;
- каждый из компонентов смеси имеет температуру, равную температуре смеси;
- каждый газ создаёт своё давление на стенки сосуда, называемое парциальным давлением.
Парциальное давление, таким образом, это давление, которое имел бы компонент смеси, если бы он один занимал весь объем смеси при той же температуре. Сумма парциальных давлений каждого компонента равна давлению смеси (закон Дальтона):
.
Парциальным объёмом компонента V
называется такой объём, который занимал
бы данный компонент при давлении, равном
давлению смеси, и температуре, равной
температуре смеси. Очевидно, что сумма
парциальных объемов равна объему смеси
(закон Амага):
.
При исследовании термодинамических процессов с газовыми смесями необходимо знать ряд характеризующих их величин: газовую постоянную, молярную массу, плотность, теплоемкость и т.д. Для их нахождения должен быть задан состав смеси, определяющий количественное содержание каждого компонента, входящего в смесь. Состав газовой смеси обычно задают массовыми, объёмными или мольными долями.
Массовой долей компонента смеси g называется величина, равная отношению массы компонента к массе всей смеси:
.
Очевидно, что масса смеси m равна сумме масс всех компонентов:
,
а сумма массовых долей:
.
Объемной долей компонента смеси ri называется величина, равная отношению парциального объема компонента к объему смеси:
.
Уравнение объёмного состава смеси имеет вид:
и сумма объемных долей:
.
Мольной долей компонента смеси хi называется величина, равная отношению числа молей этого компонента к общему числу молей смеси:
.
Очевидно, что:
.
Состав смеси задают долями единицы или в процентах. Связь между мольными и объемными долями можно установить, записывая уравнение Клапейрона – Менделеева для компонента смеси и всей смеси:
,
.
Поделив почленно первое уравнение на второе, получим:
.
Таким образом, для идеальных газов объемные и мольные доли оказываются равными.
Связь между массовыми и объёмными долями устанавливается соотношениями:
.
(5)
Из закона Авогадро следует:
,
(6)
где μ – молярная масса смеси, которую называют кажущейся. Она может быть найдена, в частности, через объемный состав смеси. Записывая уравнение Клапейрона – Менделеева для i-го компонента смеси в виде
и суммируя по всем компонентам, получим:
.
Сравнивая его с уравнением состояния для смеси в целом
,
приходим к очевидному соотношению:
.
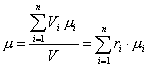Если найдена молярная масса смеси, газовая постоянная смеси может быть определена обычным способом:
.
(7)
Газовую постоянную смеси можно рассчитать и через массовые доли и газовые постоянные компонентов. Запишем для каждого компонента смеси уравнение Клапейрона:
.
Суммируя по всем компонентам, получим:
.
Сумма в левой части уравнения равна объему смеси. Поделив обе части уравнения на массу смеси m
,
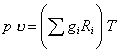замечаем, что сумма в правой части уравнения представляет собой газовую постоянную смеси:
.
С учетом (6) и (7) соотношение (5) можно дополнить:
.
Используя последнее соотношение
и производя суммирование по компонентам
,
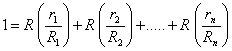получим расчетную формулу для газовой постоянной смеси через объемные доли:
.
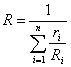Удельный объем и плотность смеси и компонентов можно найти из уравнений состояния:
и
,
и
.
В соответствии с определениями парциального давления и парциального объема можно записать:
.
Тогда парциальное давление компонента смеси:
.
Расчет теплоёмкости газовой смеси выполняют на основе данных о составе смеси и теплоёмкости каждого компонента. Массовая, объемная и мольная теплоемкости смеси рассчитываются через соответствующие доли:
- массовая теплоемкость
;
- объемная теплоемкость
;
- мольная теплоемкость
.
Этими формулами пользуются при определении истинных и средних теплоемкостей смеси.
Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре.
Для осуществления изотермического процесса систему обычно помещают в термостат (массивное тело, находящееся в тепловом равновесии),теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро по сравнению со скоростью протекания процесса, и, температура системы в любой момент практически не отличается от температуры термостата. Можно осуществить изотермический процесс иначе — с применением источников или стоков тепла, контролируя постоянство температуры с помощью термометров. К изотермическим процессам относятся, например, кипение жидкости или плавление твёрдого тела при постоянном давлении. Графиком изотермического процесса является изотерма.
В идеальном
газе при изотермическом
процессе произведение давления на объём
постоянно (закон
Бойля-Мариотта). Изотермы
идеального газа в координатах
— гиперболы, расположенные на графике
тем выше, чем выше температура, при
которой происходит процесс.
При изотермическом процессе системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа. Альтернативный процесс, при котором теплообмен с окружающей средой отсутствует (термодинамическая система находится в энергетическом равновесии — система не поглощает и не выделяет тепло), называется адиабатическим процессом.
Работа,
совершенная идеальным газом в
изотермическом процессе, равна
,
где
— число частиц газа,
— температура,
и
— объём газа в начале и конце процесса,
— постоянная
Больцмана .
В твёрдом теле и большинстве жидкостей изотермические процессы очень мало изменяют объём тела, если только не происходит фазовый переход.
Первый закон термодинамики для изотермического процесса записывается в виде:
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе идеального газа.
Согласно закону
Гей-Люссака, при изобарном
процессе в идеальном
газе
.
Работа, совершаемая газом при расширении
или сжатии газа, равна
.
Количество теплоты, получаемое или
отдаваемое газом, характеризуется
изменением энтальпии:
.
Молярная теплоёмкость при постоянном
давлении обозначается как
.
В идеальном газе она связана с теплоёмкостью
при постоянном объёме соотношением
Майера
.
Молекулярно-кинетическая теория позволяет вычислить приблизительные значения молярной теплоёмкости для различных газов через значение универсальной газовой постоянной:
для одноатомных газов
,
то есть около 20.8 Дж/(моль·К);для двухатомных газов
,
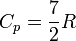то есть около 29.1 Дж/(моль·К);для многоатомных газов
,
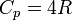то есть около 33.3 Дж/(моль·К).
Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).