Свободная энергия Гельмгольца и устойчивость термодинамического равновесия

Можно показать, что в системе с фиксированными температурой и объемом положение устойчивого равновесия соответствует точке минимума свободной энергии Гельмгольца. Другими словами, в этой точке (для такой системы) никакие изменения макроскопических параметров невозможны.

Свободная энергия Гельмгольца и максимальная работа

Свободная энергия Гельмгольца получила своё название из-за того, что она является мерой работы, которую может совершить термодинамическая система над внешними телами.

Пусть система переходит из состояния в состояние . Поскольку работа не является функцией состояния системы, работа, совершенная системой в данном процессе будет зависеть от пути, по которому этот переход будет осуществляться.

Зададимся целью определить максимальную работу, которую система может совершить в этом случае.

Можно показать, что эта максимальная работа равна убыли свободной энергии Гельмгольца :

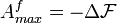• . Здесь индекс ^f означает, что рассматриваемая величина является полной работой системы в данном процессе.

Свободные энергии Гельмгольца и Гиббса

В приложениях «свободной энергией» иногда называют не свободную энергию Гельмгольца, а энергию Гиббса. Это связано с тем, что энергия Гиббса также является мерой максимальной работы, но в данном случае рассматривается только работа над внешними телами, исключая среду:

• , где — энергия Гиббса.

Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, или термодинамический потенциал в узком смысле) — это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:

Энергию Гиббса можно понимать как полную химическую энергию системы (кристалла, жидкости и т. д.)

Понятие энергии Гиббса широко используется в термодинамике и химии.

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным T ΔS, обусловленным увеличением беспорядка в системе вследствие роста ее энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж)

Определение

Классическим определением энергии Гиббса является выражение

где — внутренняя энергия, — давление, — объём, — абсолютная температура, — энтропия.

Дифференциал энергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — через давление p и температуру T:

Для системы с переменным числом частиц этот дифференциал записывается так:

Здесь — химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу.

Связь с термодинамической устойчивостью системы

Покажем, что минимум потенциала Гиббса соответствует устойчивому равновесию термодинамической системы с фиксированными температурой, давлением и числом частиц.

Запишем обобщённое уравнение первого и второго начал термодинамики:

При .

Таким образом в системе при постоянных температуре и давлении энергия Гиббса достигает минимального значения.