Частный случай: два тепловых резервуара
Пусть система I сообщается с тепловыми
резервуарами
и
температур
и
соответственно. Безразлично, какой из
них является нагревателем, а какой —
холодильником (направление передачи
тепла определяется знаком — положительным,
если оно получено системой, и иначе
отрицательным). Согласно второй теореме
Карно КПД
цикла
Карно — максимальный; для
системы I выполняется
.
Отсюда следует частный случай[2]
неравенства Клаузиуса:
(При обратимом процессе, в частности при цикле Карно, выполняется равенство.)
Общий случай: много тепловых резервуаров
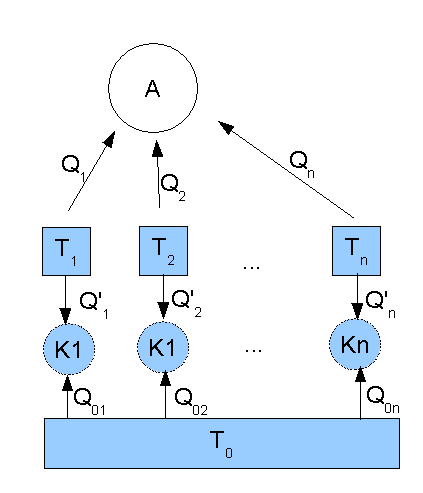
Для получения неравенства Клаузиуса в
общем виде можно рассмотреть систему
A, работающую с n резервуарами температур
и получающую от них тепло
.
Вводится дополнительный Резервуар
температуры
.
Между ним и остальными резервуарами
запускаются машины Карно — по одной на
каждый.
По вышедоказанному равенству для двухрезервуарной обратимой системы выполняется
.
Циклы Карно проводятся таким образом,
чтобы передавать резервуарам столько
тепла, сколько они передали системе A:
.
Тогда
.
Это тепло отдаст резурвуар температуры
,
в то время как состояние остальных
резервуаров вернётся к исходному.
Следовательно, рассмотренный процесс
эквивалентен процессу передачи тепла
резурвуаром температуры
системе A, причём совокупность «система
A — резервуар
»
теплоизолирована. Следовательно, по
первому
началу термодинамики
системой A совершена работа
.
В соответствии с формулировкой
Томсона второго начала термодинамикиэта
работа не может быть положительной.
Отсюда очевидно неравенство Клаузиуса
в общем виде:
Следствия
Неравенство Клаузиуса даёт ввести понятие энтропии.
Энтропия системы — функция её состояния, определённая с точностью до произвольной постоянной. Разность энтропий в двух равновесных состояниях 1 и 2 по определению равна приведённому количеству теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути.
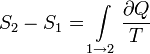
Из неравенства Клаузиуса и определения энтропии непосредственно следует эквивалентный второму началу термодинамики
Закон возрастания энтропии. Энтропия адиабатически изолированной системы либо возрастает, либо остаётся постоянной.