Следствия Недостижимость абсолютного нуля температур

Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достичь ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться, поэтому третье начало термодинамики иногда формулируют как принцип недостижимости абсолютного нуля температуры.

Поведение термодинамических коэффициентов

Из третьего начала термодинамики вытекает ряд термодинамических следствий: при должны стремиться к нулю теплоёмкости при постоянном давлении и при постоянном объёме, коэффициенты теплового расширения и некоторые аналогичные величины. Справедливость третьего начала термодинамики одно время подвергалась сомнению, но позже было выяснено, что все кажущиеся противоречия (ненулевое значение энтропии у ряда веществ при ) связаны с метастабильными состояниями вещества, которые нельзя считать термодинамически равновесными.

Нарушения третьего начала термодинамики в моделях

Третье начало термодинамики часто нарушается в модельных системах. Так, при энтропия классического идеального газа стремится к минус бесконечности. Это говорит о том, что при низких температурах уравнение Менделеева — Клапейрона неадекватно описывает поведение реальных газов.

Таким образом, третье начало термодинамики указывает на недостаточность классической механики и статистики и является макроскопическим проявлением квантовых свойств реальных систем.

В квантовой механике, тем не менее, в модельных системах третье начало также может нарушаться. Таковы все случаи, когда применяется распределение Гиббса и основное состояние является вырожденным.

Несоблюдение третьего начала в модели, однако, не исключает того, что в каком-то диапазоне изменения физических величин эта модель может быть вполне адекватна.

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия становится функцией не только температуры, но и объёма.

Уравнение Ван-дер-Ваальса — это одно из широко известных приближённых уравнений состояния, имеющее компактную форму и учитывающее основные характеристики газа с межмолекулярным взаимодействием^[

Уравнение состояния

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

где

• — давление,

• — молярный объём,

• — абсолютная температура,

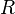• — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка — объем молекул газа.

Для молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

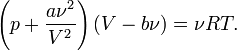
где

• — объём