Уравнение Пуассона для идеального газа Адиабата Пуассона

Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением

где — его объём, — показатель адиабаты, и — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

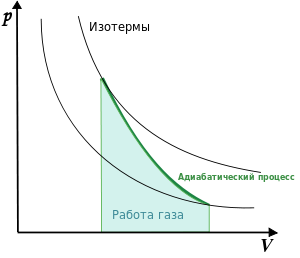
График адиабаты (жирная линия) на диаграмме для газа. — давление газа; — объём.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду

где — абсолютная температура газа. Или к виду

Поскольку всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении ) газ нагревается ( возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент .

Вывод уравнения

Согласно закону Менделеева — Клапейрона справедливо соотношение

где R — универсальная газовая постоянная. Продифференцировав обе части, получаем

Если в (3) подставить из (2), а затем из (1), получим

или, введя коэффициент :

.

Это уравнение можно переписать в виде

что после интегрирования даёт уравнение

.

Окончательно получаем

что и требовалось доказать.

Показатель адиабаты

При адиабатическом процессе показатель адиабаты равен .

Для нерелятивистского невырожденного одноатомного идеального газа ^[19], для двухатомного ^[19], для трёхатомного , для газов, состоящих из более сложных молекул, показатель адиабаты определяется числом степеней свободы (i) конкретной молекулы, исходя из соотношения .

Для реальных газов показатель адиабаты отличается от показателя адиабаты для идеальных газов, особенно для низких температур, когда большую роль начинает играть межмолекулярное взаимодействие. Для его теоретического нахождения следует проводить расчёт без некоторых допущений, в частности, использованных при выводе формулы (1) и использовать формулу (1а).

Один из методов для экспериментального определения показателя был предложен в 1819 г. Клеманом и Дезормом. Стеклянный баллон вместимостью несколько литров наполняется исследуемым газом при давлении . Затем открывается кран, газ адиабатически расширяется, и давление падает до атмосферного — . Затем происходит его изохорноенагревание до температуры окружающей среды. Давление повышается до . В результате такого эксперимента k можно вычислить как

Энтропия и обратимость

В общем случае для произвольной физической системы изменение состояния при адиабатическом расширении определяется производными термодинамических параметров при постоянной энтропии. Справедливы соотношения

,

,

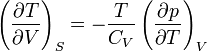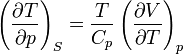где C_p и C_v — теплоёмкости при постоянном давлении и объёме, которые всегда положительны по своему физическому смыслу, — обозначение частной производной. Как и при определении молярной теплоёмкости, при расчёте частной производной находится изменения параметра в числителе, которое происходят только под действием изменения параметра, стоящего в знаменателе. Пусть система адиабатически расширяется, то есть . Тогда если коэффициент теплового расширения положительный, изменение температуры должно быть отрицательным. То есть, температура системы будет уменьшатся при адиабатическом расширении, если коэффициент теплового расширения положителен, и увеличиваться в противоположном случае^[21]. Примером подобного процесса является эффект Джоуля — Томсона, который также является необратимым адиабатическим процессом^[22].

Необратимость адиабатических процессов связана с неравновесным переходом от начального состояния к конечному: система не следует адиабате Пуассона , поэтому точный путь системы в координатах термодинамичесих величин не может быть указан. К необратимости может привести наличие внутреннего трения в газе, которое изменит энтропию системы. Так как выделяемое при изменении энтропии тепло не покидает систему (отсутствие обмена теплом с окружающей средой может быть навязано помещением системы в термостат), меняется температура газа. Изменение энтропии необратимого процесса из состояния A в состояние B можно рассчитать, соединив их на диаграмме несколькими отрезками путей, соответствующих обратимым процессам. Примерами необратимых адиабатических процессов являются дросселирование и смешение двух газов, первоначально находившихся при разных температурах и давлениях внутри поделённого пополам термостата.