Термодинамическими величинами называют физические величины, применяемые при описании состояний и процессов в термодинамических системах.

Функции состояния зависят только от текущего состояния системы и не зависят от пути, по которому система пришла в это состояние.

Функции состояния в термодинамике включают:

• температуру,

• давление,

• объём,

• энтропию,

а также термодинамические потенциалы.

В зависимости от выбранной модели некоторые из этих величин, строго говоря, могут быть не функциями, а независимыми переменными.

Эти величины не являются независимыми. Связь между термодинамическими параметрами для конкретной системы называется уравнением состояния.

В случае, если известно каноническое уравнение состояния, задание любой пары параметров из следующих:

• энтропия и объём,

• энтропия и давление,

• температура и объём,

• температура и давление,

позволяет вычислить остальные два параметра.

Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние.

Функции процесса в термодинамике включают:

• количество теплоты и

• термодинамическую работу.

Эти величины, однако, могут быть «превращены» в функции состояния с помощью интегрирующего множителя:

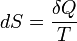• , где 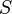(энтропия) — функция состояния.

• , где (давление) и 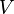(объём) — функции состояния.

Термодинамические потенциалы (термодинамические функции) — характеристические функции в термодинамике, убыль которых в равновесных процессах, протекающих при постоянстве значений соответствующих независимых параметров, равна полезной внешней работе.

Выделяют следующие термодинамические потенциалы:

• внутренняя энергия

• энтальпия

• свободная энергия Гельмгольца

• потенциал Гиббса

• большой термодинамический потенциал

Внутренняя энергия

Определяется в соответствии с первым началом термодинамики, как разность между количеством теплоты, сообщенным системе, и работой, совершенной системой над внешними телами:

.

Энтальпия

Определяется следующим образом:

,

где — давление, а — объём.

Поскольку в изобарном процессе работа равна , приращение энтальпии в квазистатическом изобарном процессе равно количеству теплоты, полученному системой.

Свободная энергия Гельмгольца

Также часто называемая просто свободной энергией. Определяется следующим образом:

,

где — температура и — энтропия.

Поскольку в изотермическом процессе количество теплоты, полученное системой, равно , то убыль свободной энергии в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Потенциал Гиббса

Также называемый энергией Гиббса, термодинамическим потенциалом, свободной энергией Гиббса и даже просто свободной энергией (что может привести к смешиванию потенциала Гиббса со свободной энергией Гельмгольца):

.

Термодинамические потенциалы и максимальная работа

Внутренняя энергия представляет собой полную энергию системы. Однако второе начало термодинамики запрещает превратить всю внутреннюю энергию в работу.

Можно показать, что максимальная полная работа (как над средой, так и над внешними телами), которая может быть получена от системы в изотермическом процессе, равна убыли свободной энергии Гельмгольца в этом процессе:

,

где — свободная энергия Гельмгольца.

В этом смысле представляет собой свободную энергию, допускающую преобразование в работу. Оставшаяся часть внутренней энергии может быть названа связанной.

В некоторых приложениях приходится различать полную и полезную работу. Последняя представляет собой работу системы над внешними телами, исключая среду, в которую она погружена. Максимальная полезная работа системы равна

где — энергия Гиббса.

В этом смысле энергия Гиббса также является свободной.

Каноническое уравнение состояния

Задание термодинамического потенциала некоторой системы в определенной форме эквивалентно заданию уравнения состояния этой системы.

Соответствующие дифференциалы термодинамических потенциалов:

• для внутренней энергии

,

• для энтальпии

,

• для свободной энергии Гельмгольца

,

• для потенциала Гиббса

.

Эти выражения математически можно рассматривать как полные дифференциалы функций двух соответствующих независимых переменных. Поэтому естественно рассматривать термодинамические потенциалы как функции:

,

,

,

.

Задание любой из этих четырёх зависимостей — то есть конкретизация вида функций , , , — позволяет получить всю информацию о свойствах системы. Так, например, если нам задана внутренняя энергия как функция энтропии и объёма , оставшиеся параметры могут быть получены дифференцированием:

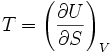
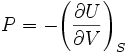
Здесь индексы и означают постоянство второй переменной, от которой зависит функция. Эти равенства становятся очевидными, если учесть, что .

Задание одного из термодинамических потенциалов как функции соответствующих переменных, как записано выше, представляет собой каноническое уравнение состояния системы. Как и другие уравнения состояния, оно справедливо лишь для состояний термодинамического равновесия. В неравновесных состояниях эти зависимости могут не выполняться.

Метод термодинамических потенциалов. Соотношения Максвелла

Метод термодинамических потенциалов помогает преобразовывать выражения, в которые входят основные термодинамические переменные и тем самым выражать такие «трудно наблюдаемые» величины, как количество теплоты, энтропию, внутреннюю энергию через измеряемые величины — температуру, давление и объём и их производные.

Рассмотрим опять выражение для полного дифференциала внутренней энергии:

.

Известно, что если смешанные производные существуют и непрерывны, то они не зависят от порядка дифференцирования, то есть

.

Но и 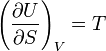, поэтому

.

Рассматривая выражения для других дифференциалов, получаем:

,

,

.

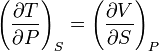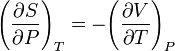Эти соотношения называются соотношениями Максвелла. Заметим, что они не выполняются в случае разрывности смешанных производных, что имеет место при фазовых переходах1-го и 2-го рода.

Потенциалы и термодинамическое равновесие

В состоянии равновесия зависимость термодинамических потенциалов от соответствующих переменных определяется каноническим уравнением состояния этой системы. Однако в состояниях, отличных от равновесного, эти соотношения теряют силу. Тем не менее, для неравновесных состояний термодинамические потенциалы также существуют.

Таким образом, при фиксированных значениях своих переменных потенциал может принимать различные значения, одно из которых соответствует состоянию термодинамического равновесия.

Можно показать, что в состоянии термодинамического равновесия соответствующее значение потенциала минимально. Поэтому равновесие является устойчивым.

Нижеприведённая таблица показывает, минимуму какого потенциала соответствует состояние устойчивого равновесия системы с заданными фиксированными параметрами.

фиксированные параметры	термодинамический потенциал
S,V,N	внутренняя энергия
S,P,N	энтальпия
T,V,N	свободная энергия Гельмгольца
T,P,N	потенциал Гиббса
T,V,	Большой термодинамический потенциал
S,P,	связанная энергия

Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:

где

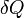• — подведённое к телу количество теплоты, измеренное в джоулях

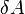• ^[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях

Эта формула является математическим выражением первого начала термодинамики

Для квазистатических процессов выполняется следующее соотношение:

где

• — температура, измеренная в кельвинах

• — энтропия, измеренная в джоулях/кельвин

• — давление, измеренное в паскалях

• — химический потенциал

• — количество частиц в системе