1.3. Расчёт полного тока трёхфазного короткого замыкания через 0,2 с после возникновения короткого замыкания методом расчётных кривых.

Данный метод основан на применении специальных кривых, которые дают для произвольного момента переходного процесса значение периодической составляющей тока в месте КЗ в функции от расчётного индуктивного сопротивления:

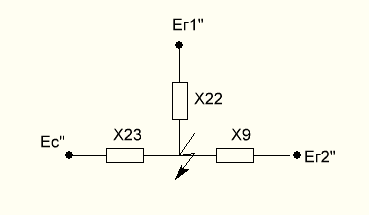
Рисунок 7 - Схема, позволяющая определить ток от источника методом расчётных кривых

В общем случае для расчёта полного тока методом расчётных кривых необходимо составить схему замещения без учёта нагрузок. Исключение составляют крупные синхронные компенсаторы и двигатели, находящиеся вблизи точки КЗ, которые в таком случае рассматриваются как генераторы равновеликой мощности. Итак, без учёта нагрузки получим следующую схему замещения:

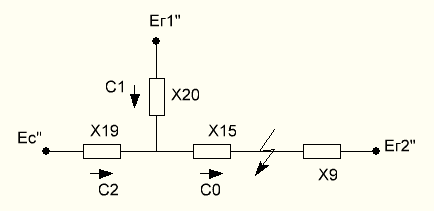
Для каждой выделенной ветви определим коэффициент токораспределения:

С₀ = 1;

С₁ = = = 0,4;

С₂ = = = 0,6.

Определим величину эквивалентных сопротивлений без учета нагрузки:

Х₁₉=0,2 (о.е);

Х₂₀=Х₈+Х₁₄= 0,28+0,06=0,34 (о.е);

X₂₁ = = = 0,12 (о.е.);

Х_экв.= X₂₁+Х₁₅=0,12+0,06=0,18 (о.е.).

Определяем взаимные сопротивления генератора Г1 и системы:

Х_ВЗГ1=Х₂₂ = = = 0,45 (о.е.);

Х_ВЗC=Х₂₃ = = = 0,3 (о.е.).

Определим расчетные сопротивления генераторов Г1 и Г2:

Х_РАСЧ = Х_ВЗ * ;

Х_{РАСЧ Г1} = Х₉ * = 0,45* = 0,28 (о.е.);

Х_{РАСЧ Г2} = Х₉ * = 0,28 * = 0,176 (о.е.).

Относительные значения периодической составляющей тока КЗ через 0,2 секунды после его возникновения определяем по расчётным кривым:

• для ветви с генератором Г1 I _{*Пτ Г1} = 3,4 (по расчетным кривым);

• для ветви с генератором Г2 I _{*Пτ Г2} = 12,8 (по расчетным кривым).

Ток от источника бесконечной мощности определится следующим образом:

Ic = = = 22,67 (кА).

Теперь найдём искомую величину периодической слагающей тока короткого замыкания для заданного момента времени 0,2 с в именованных единицах:

I пτ = I _{*Пτ Г1} * + I _{*Пτ Г2} * + Ic ;

I пτ = 3,4* + 2,8 * + 22,67=49,51 (кА).

Теперь рассчитаем значения апериодической составляющей тока КЗ к моменту времени 0,2 с для каждой ветви.

Iaτ = * I_ПО * e ^–t/Ta

Апериодическая составляющая тока КЗ в ветви с генератором Г1:

Iaτ_Г1 = * I_ПОГ1 * e ^–t/Taг1 = 2,04 * = 1,79 (о.е).

Апериодическая составляющая тока КЗ в ветви с генератором Г2:

Iaτ_Г2 = * I_ПОГ2 * e ^–t/Taг2 = 3,85 * = 3,3 (о.е).

Апериодическая составляющая тока КЗ от системы:

Iaτ_С = * I_ПОС * e ^–t/Taс = 3,33 * = 0,067 (о.е).

Апериодическая составляющая тока через 0,2 с в точке КЗ в именнованных единицах:

Iaτ_∑ = Iaτ_Г1*I_б + Iaτ_Г2 *I_б + Iaτc *I_б = 1,79*6,8 + 3,3*6,8 + 0,067*6,8 = 35,07 (кА).

Полный ток в месте КЗ через 0,2 с в именованных единицах:

I _kτ = = 60,6 (кА).

2. Расчёт токов несимметричных коротких замыканий

2.1 Составление схем замещения отдельных последовательностей

Для определения токов и напряжений при несимметричных КЗ используется метод симметричных составляющих и уравнения второго закона Кирхгофа. Полученные на этой основе формулы приводят к правилу эквивалентности прямой последовательности, показывающему, что ток прямой последовательности любого несимметричного КЗ может быть определён как ток при трёхфазном КЗ в точке, удалённой от действительной точки КЗ на дополнительное сопротивление, определяемое видом КЗ.

Для расчёта дополнительного сопротивления необходимо знать эквивалентные сопротивления схем замещения для токов обратной и нулевой последовательностей относительно точки КЗ, поэтому расчёт несимметричных КЗ следует начинать с составления соответствующих схем замещения.

Схема замещения прямой последовательности идентична схеме, составленной для расчёта токов трёхфазного короткого замыкания. Отличие только в том, что в точке КЗ подключен условный источник с напряжением, равным напряжению прямой последовательности в точке КЗ. Для определения сверхпереходного и ударного тока генераторы, двигатели и обобщённая нагрузка вводятся своими сверхпереходными ЭДС и сопротивлениями.

Поскольку напряжение прямой последовательности в любой точке схемы при несимметричном КЗ всегда выше, чем при трёхфазном коротком замыкании в том же месте, то подпитывающий эффект нагрузки и двигателей при несимметричных КЗ проявляется слабее, чем при трёхфазных. Поэтому при определении ударного тока несимметричного КЗ можно пренебречь нагрузками и двигателями за исключением достаточно мощных двигателей, непосредственно подключенных к точке КЗ.

Исключим из исходной схемы замещения нагрузку Н1 и Н2 и вновь свернём её относительно точки КЗ.

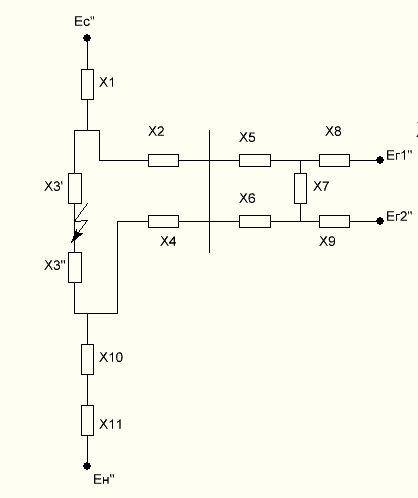
Рисунок 8 - Схема замещения системы для токов прямой последовательности без учёта нагрузки

Х₁=0,14 (о.е);

Х₂=0,05 (о.е);

Х`₃=0,07*0,75=0,053 (о.е);

Х``₃=0,07*0,25=0,017 (о.е);

Х₄=0,14 (о.е);

Х₇=0,27 (о.е);

Х₈=0,28 (о.е);

Х₉=0,28 (о.е);

X ₁₀ =X_T3*(Б) = = = 0,053 (о.е.);

X₁₁=X _н5*(Б)= = = 1,75 (о.е.).

Х₆=Х₇=

Сворачиваем схему замещения относительно точки КЗ. Для схемы замещения на рисунке 14 проведём преобразования для сопротивлений, соединённых последовательно:

X₁₂ = X ₁₁ + X ₁₀ = 1,75 + 0,053= 1,803 (о.е.).

Очевидно, что сопротивления Х₆, Х₅ и Х₇ окажутся соединёнными в треугольник. Тогда:

Х₁₃=0,02 (о.е);

Х₁₄=0,06 (о.е);

Х₁₅=0,06 (о.е).

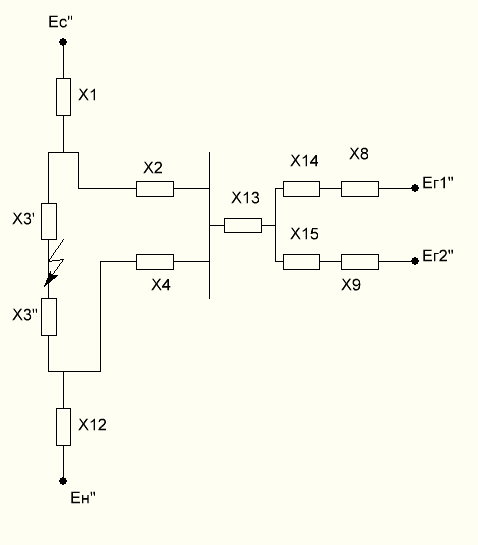
Как видно из схемы замещения, сопротивления Х_14, Х₈ и Х₁₅, Х₉ соединены соответственно последовательно. Тогда:

X₁₆ = X ₁₄ + X ₈ = 0,06 + 0,28= 0,34 (о.е.);

X₁₇ = X ₁₅ + X ₉ = 0,06 + 0,28= 0,34 (о.е.).

Видно, что сопротивления Х₁₆ и Х₁₇ соединены параллельно и последовательно с Х₁₃. Тогда:

X₁₈= = = 0,19 (о.е.).

Определим эквивалентную ЭДС генераторов:

E_г1,г2’’ = = = 1,08 (о.е.).

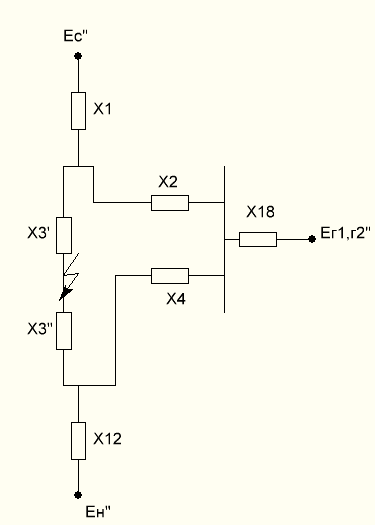
Из схемы замещения видно, что сопротивления Х₂, Х₄, и Х₁₈ соединены в звезду, нужно преобразовать звезду в треугольник.

X₁₉ = X ₁₈ + X ₂ + = 0,19 + 0,05+ = 0,31 (о.е.);

X₂₀ = X ₄ + X ₂ + = 0,14 + 0,05+ = 0,23 (о.е.);

X₂₁ = X ₄ + X ₁₈ + = 0,14 + 0,19+ = 0,86 (о.е.).

Разрываем Е_Г1,Г2`` и получается, что сопротивления Х₁₉ параллельно

Х₁, сопротивление Х₂₁ параллельно Х_12.

X₂₂= = = 0,09 (о.е.);

X₂₃= = = 0,6 (о.е.).

Сэквивалентируем ЭДС:

E_гс’’ = = = 0,22 (о.е.);

E_гн’’ = = = 1 (о.е.).

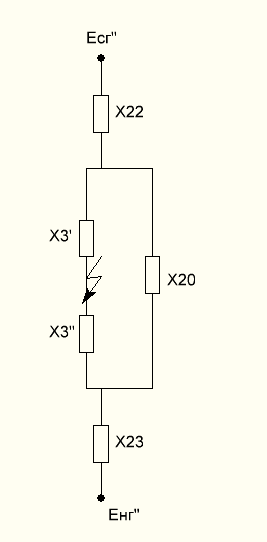
Сопротивления Х`₃ ,Х₃`` и Х₂₀ образуют треугольник, который нужно преобразовать в звезду.

X₂₄= = = 0,04 (о.е.);

X₂₅= = = 0,01 (о.е.);

X₂₆= = = 0,003 (о.е.).

Сопротивления X_24, X₂₂ и X₂₅, X₂₃ соответственно соединены последовательно.

X₂₇ = X ₂₂ + X ₂₄ = 0,09 + 0,04= 0,13 (о.е.);

X₂₈ = X ₂₅ + X ₂₃ = 0,01 + 0,6= 0,61 (о.е.).

Сопротивления X₂₇ и X₂₈ параллельны:

X₂₉= = = 0,11 (о.е.).

Эквивалентная ЭДС:

E_экв’’ = = = 0,36 (о.е.).

Получили следующую схему замещения:

Определим эквивалентное сопротивление относительно точки КЗ:

X _1экв = X ₂₆ + X ₂₉ = 0,003 + 0,11= 0,113 (о.е.).

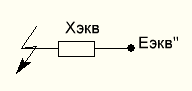
Рисунок 9 - Эквивалентная схема замещения

Найдем эквивалентное активное сопротивление прямой последовательности.

При определении эквивалентного активного сопротивления, ЭДС не считаем.

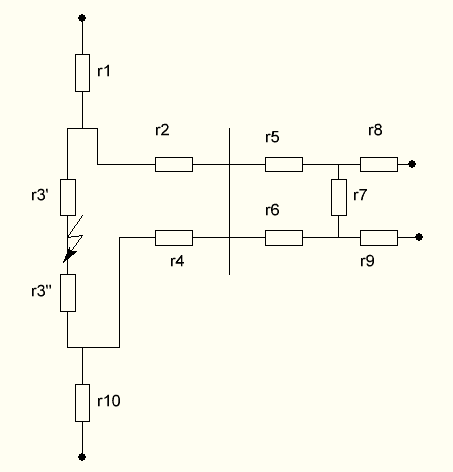
Рисунок 10 - Исходная схема замещения, для определения эквивалентного активного сопротивления

Сначала находим все активные сопротивления.

1. Автотрансформатор:

r₁ = = = 0,0025 (о.е.).

2. Воздушные линии:

r₂ = * r₀ * L * = *0,118*30* = 0,015 (о.е.);

r’₃ = * r₀ * L*0,75 * = 1*0,118*0,75*20* = 0,015 (о.е.);

r”₃ = * r₀ * L *0,25* = 1*0,118*0,25*20* = 0,005 (о.е.);

r₄ = * r₀ * L * = 1*0,118*40* = 0,04 (о.е.).

3. Трансформаторы:

r₅ = r₆ = = = 0,003 (о.е.);

r₁₀=r_T3B*(Б) = = = 0,32 (о.е.).

7. Реактор:

r₇ = = = 0,0027 (о.е.).

8. Генераторы:

r₈ = r₉ = = = 0,0022 (о.е.).

Начинаем эквивалентировать схему к точке КЗ.

Эквивалентирование аналогично экивалентированию схемы с индуктивными сопротивлениями.

Сопротивления r₅, r₆ и r₇ соединены в треугольник, их сэквивалентируем в звезду. Тогда:

r₁₂= = = 0,001 (о.е.);

r₁₃= = = 0,0009 (о.е.);

r₁₄= = = 0,0009 (о.е.);

r₁₅= r₁₃+ r₈= 0,0009 + 0,0022 = 0,00031 (о.е.);

r₁₆= r₁₄+ r₉= 0,0009 + 0,0022 = 0,00031 (о.е.).

Сопротивления r₁₅ и r₁₆ параллельны.

r₁₇ = = = 0,000155 (о.е.).

Получили следующую схему замещения:

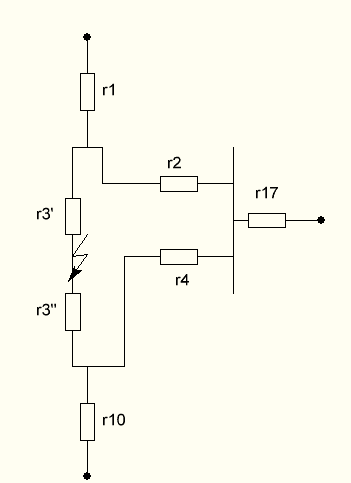
Сопротивления r₂ ,r₄ и r₁₇ образуют звезду, которую можно преобразовать в треугольник.

r₁₈= r₂+ r₁₇+ = 0,015 + 0,000155 + = 0,017 (о.е.);

r₁₉= r₄+ r₁₇+ = 0,04 + 0,000155 + = 0,046 (о.е.);

r₂₀= r₄+ r₂+ = 0,04 + 0,000155 + = 0,44 (о.е.).

Разрываем сеть и получаем, что r₁₈ параллельно r₁, а r₁₉ параллельно r_2.

r₂₁ = = = 0,002 (о.е.);

r₂₂ = = = 0,19 (о.е.).

Получили схему замещения:

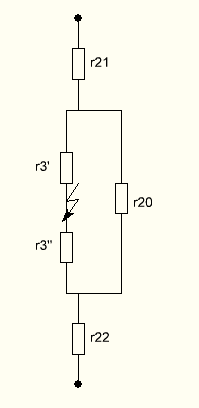
Сопротивления r₂₀, r`₃ и r``₃ образуют треугольник относительно точки короткого замыкания. Эквивалентируем треугольник в звезду.

r₂₃= = = 0,014 (о.е.);

r₂₄= = = 0,004 (о.е.);

r₂₄= = = 0,00016 (о.е.).

Сопротивления r_23, r₂₁ соединены последовательно, r_22, r₂₄ соединены последовательно, а между собой они параллельны. Тогда получим:

r₂₆= r₂₁+ r₂₃= 0,002 + 0,014 = 0,016 (о.е.);

r₂₇= r₂₄+ r₂₂= 0,004 + 0,19 = 0,194 (о.е.);

r₂₈ = = = 0,015 (о.е.).

Получаем эквивалентное сопротивление:

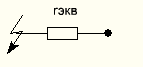
r _1экв= r₂₅+ r₂₈= 0,00016 + 0,015 = 0,01516 (о.е.).

Схема замещения обратной последовательности по структуре аналогична схеме прямой последовательности, но ЭДС генерирующих элементов в ней отсутствуют; к точке КЗ подключен условный источник с напряжением, равным напряжению обратной последовательности в точке КЗ.

Принципиально сопротивления обратной и прямой последовательностей элементов с вращающимися магнитосвязанными цепями (синхронные и асинхронные машины) не равны. Однако поскольку это неравенство само по себе незначительно, мало влияет на результирующее сопротивление схемы, им в практических расчётах часто пренебрегают. Так поступим и в данной работе. Следовательно, сопротивления всех элементов схем прямой и обратной последовательностей будут равны, значит X_1∑ = X_2∑ = 0,113 (о.е.),

r_1∑ = r_2∑ = 0,01516 (о.е.) , и рассчитывать результирующее сопротивление схемы обратной последовательности не нужно.

Рисунок 11 - Эквивалентная схема замещения системы для токов обратной последовательности

Схема нулевой последовательности отличается от схем прямой и обратной последовательностей. Ток нулевой последовательности, по существу, является однофазным током, разветвлённым между тремя фазами и возвращающимся через землю и параллельные ей цепи. Поэтому путь токов нулевой последовательности резко отличается от пути токов прямой и обратной последовательности. Конфигурация схемы нулевой последовательности определяется соединением обмоток трансформаторов и режимом работы их нейтралей (заземлённая или изолированная нейтраль). При отсутствии емкостной проводимости (этой проводимостью в схемах, рассматриваемых в данной работе, можно пренебречь) токи нулевой последовательности потекут лишь в сторону элементов, электрически связанных с точкой КЗ, обмотки фаз которых соединены в звезду с заземлённой нейтралью. Следовательно, только эти элементы войдут в схему нулевой последовательности. Протекая по обмоткам трансформаторов, соединённым в звезду с заземлённой нейтралью, токи нулевой последовательности наводят в других обмотках трансформаторов ЭДС нулевой последовательности. Но ток нулевой последовательности возникает в этих обмотках, если они соединены в треугольник (при этом ток будет циркулировать по треугольнику, не выходя из него) или в звезду с заземлённой нейтралью, к которой подключен элемент, также имеющий заземлённую нейтраль.

В данной работе принимается, что обмотки генераторов, обобщённой нагрузки соединены в треугольник или в звезду с изолированной нейтралью. Поэтому эти элементы в схему замещения нулевой последовательности входить не будут. Сопротивления нулевой последовательности трансформаторов и автотрансформаторов определяются их конструкцией и соединением обмоток.

Таким образом, составим схему замещения нашей системы без учёта генераторов и нагрузки. На схеме опустим индексы _*0(б), указывающие на то, что это сопротивления нулевой последовательности, выраженные в относительных единицах с приведением к базисным условиям схемы

Проведём пересчёт сопротивлений линий для нулевой последовательности:

X ₃ = 0,05 * 4,7 = 0,235 (о.е.);

X` ₄ = 0,053 * 4,7 = 0,25 (о.е.);

X`` ₄ = 0,017 * 4,7 = 0,08 (о.е.;)

X ₅ = 0,014 * 4,7 = 0,658 (о.е.).

Сопротивление автотрансформатора:

X ₁ = X _ТВ =0,14 (о.е.);

X ₂ = X _ТН = = = 0,31 (о.е.).

Сопротивления трансформаторов Т1 и Т2 осталось прежним :

Х₆=Х₇=Х_т1=Х_Т2=0,11 (о.е).

Сопротивление трансформатора Т3:

Х₈=Х_Т3=0,053 (о.е).

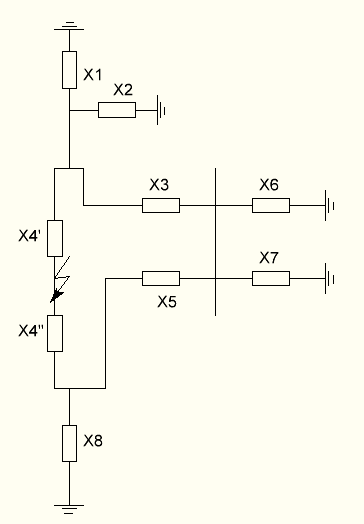
Рисунок 12 - Исходная схема замещения системы для токов нулевой последовательности

Сворачиваем данную схему относительно точки возникшей несимметрии. В расчётах будем опускать индекс ₀, подразумевая, что все расчёты ведутся для сопротивлений нулевой последовательности.

Вычислим сопротивление обмоток ВН и НН автотрансформатора АТ-4 и трансформаторов Т1 и Т2 включенных на параллельную работу:

X₉= = = 0,055 (о.е.);

X₁₀= = = 0,096 (о.е.).

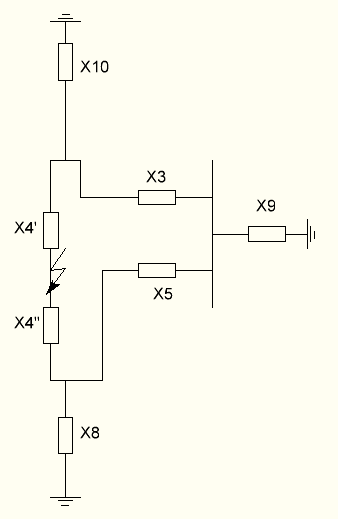
Преобразуем звезду сопротивлений Х₉ - Х₃ - Х₅ в эквивалентный треугольник:

X₁₁= X ₃ + X ₉ + = 0,235 + 0,055 = 0,31 (о.е.);

X₁₂= X ₅ + X ₉ + = 0,658 + 0,055 = 0,87 (о.е.);

X₁₃= X ₃ + X ₅ + = 0,235 + 0,658 = 3,7 (о.е.).

Параллельные сопротивления равны:

X₁₄= = = 0,07 (о.е.);

X₁₅= = = 0,05 (о.е.).

Получаем схему:

Проведём преобразование треугольника сопротивлений Х₁₃-Х`₄-Х``₄ в звезду. Сопротивления звезды:

X₁₆ = = = 0,23 (о.е.);

X₁₇ = = = 0,07 (о.е.);

X₁₈ = = = 0,005 (о.е.).

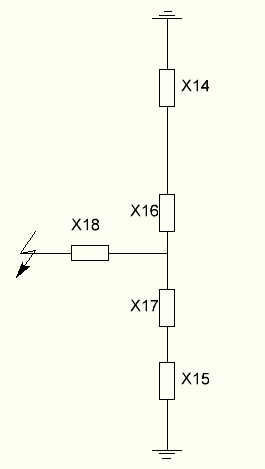
Находим эквивалентное сопротивление:

X экв0 = + X ₁₈ = + 0,005= 0,09 (о.е.)

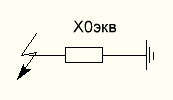
Рисунок 13 - Эквивалентная схема замещения для нулевой последовательности

Расчет активного сопротивления.

Проведём пересчёт сопротивлений линий для нулевой последовательности:

r₃ = 0,015 * 4,7 = 0,0705 (о.е.);

r` ₄ = 0,015 * 4,7 = 0,0705 (о.е.);

r`` ₄ = 0,005 * 4,7 = 0,0235 (о.е.;)

r ₅ = 0,04 * 4,7 = 0,188 (о.е.).

Сопротивление автотрансформатора:

r ₁ = r _ТВ =0,0025 (о.е.);

r₂ = r_АТН = = = 0,0007(о.е.)

Сопротивления трансформаторов Т1 и Т2 осталось прежним :

r₆=r₇=r_т1=r_Т2=0,003 (о.е).

Сопротивление трансформатора Т3:

Х₈=Х_Т3=0,32 (о.е).

Рисунок 14 - Исходная схема замещения системы для токов нулевой последовательности

Сворачиваем данную схему относительно точки возникшей несимметрии. В расчётах будем опускать индекс ₀, подразумевая, что все расчёты ведутся для сопротивлений нулевой последовательности.

Вычислим сопротивление обмоток ВН и НН автотрансформатора АТ-4 и трансформаторов Т1 и Т2 включенных на параллельную работу:

r₉= = = 0,0015 (о.е.);

r₁₀= = = 0,0005 (о.е.).

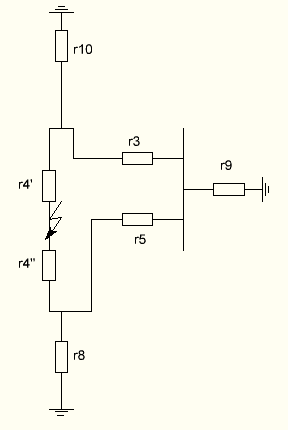
Преобразуем звезду сопротивлений r₉ - r₃ - r₅ в эквивалентный треугольник:

r₁₁= r ₃ + r ₉ + = 0,0705 + 0,0015 = 0,072 (о.е.);

r₁₂= r ₅ +r ₉ + = + 0,0015 = 0,1935 (о.е.);

r₁₃= r ₃ + r ₅ + = 0,0705 + = 9,09 (о.е.).

Параллельные сопротивления равны:

r₁₄= = = 0,0005 (о.е.);

r₁₅= = = 0,12 (о.е.).

Получаем схему:

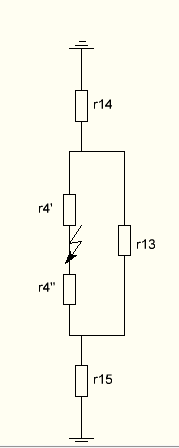
Проведём преобразование треугольника сопротивлений r₁₃-r`₄-r``₄ в звезду. Сопротивления звезды:

r₁₆ = = = 0,07 (о.е.);

r₁₇ = = = 0,023 (о.е.);

r₁₈ = = = 0,00018 (о.е.).

Находим эквивалентное сопротивление:

r_oэкв = + r ₁₈ = + 0,00018 = 0,0002 (о.е.)

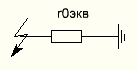
Рисунок 15 - Эквивалентная схема замещения для нулевой последовательности

2.2 Расчёт ударного тока при однофазном и двухфазном КЗ

Однофазное короткое замыкание

Рассчитаем дополнительное сопротивление для однофазного КЗ:

x_∆ = x_2∑ + x_0∑ = 0,113 + 0,09 = 0,203 (о.е.);

r_∆ = r_2∑ + r_0∑ = 0,01516 + 0,0002 = 0,01536 (о.е.).

Таким образом, ток прямой последовательности в месте однофазного КЗ:

I_П0А1 = * I_Б1= * 6,8 = 7,75 (кА).

Коэффициент для однофазного КЗ . Ударный ток в месте КЗ определяем по той же формуле, что и для симметричного короткого замыкания:

i_У = * I_П0А1 * m * K_УД.

Ударный коэффициент может быть найден по формуле:

где постоянная времени:

Ta = = = 0,033 (с);

K_УД = 1 + = 1 + = 1,74.

Ударный ток в именованных единицах:

i_У = * I_П0А1 * m * K_УД = * 7,75 * 3 * 1,74= 57,21 (кА).

Двухфазное короткое замыкание на землю

Рассчитаем дополнительное сопротивление для двухфазного КЗ на землю:

x_∆ = = = 0,05 (о.е.);

r_∆ = = = 0,00019 (о.е.).

Таким образом, ток прямой последовательности в месте двухфазного КЗ на землю:

I_П0А1 = * I_Б1= * 6,8 = 15 (кА).

Коэффициент для двухфазного КЗ на землю:

m = * = * = 1,5.

Ударный коэффициент может быть найден по формуле:

где постоянная времени:

Ta = = = 0,034 (с);

K_УД = 1 + = 1 + = 1,75.

Ударный ток в именованных единицах:

i_У = * I_П0А1 * m * K_УД = * 15 * 1,5 * 1,75 = 55,68 (кА).

2.2. Построение векторных диаграмм токов и напряжений в точке КЗ.

Точка M отмечена на схеме электрической системы (рисунок 1).

Расчёт симметричных составляющих тока и напряжения в точке короткого замыкания.

Расчёт тока прямой последовательности в месте КЗ для заданного момента времени методом расчётных кривых производится аналогично расчёту трёхфазного КЗ, но с учётом дополнительного сопротивления .

Однофазное короткое замыкание.

Токи прямой, обратной и нулевой последовательности одинаковы и равны:

I _КА1 = I _КА2 = I _КА0 = 7,75 (кА).

I _КА = 3 * I _КА1 = 3 * 7,75 = 23,25 (кА).

I _КB = I _КC = 0 (кА).

Напряжения обратной, нулевой и прямой последовательности:

U_КА2 = * X_2∑ * U_Б1 = * 0,113 * 121 = 15,6 (кВ);

U_КА0 = * X_0∑ * U_Б1 = * 0,09 * 121 = 12,4 (кВ);

U _КА1 = - (U _КА2 + U _КА0) = - (15,6 + 12,4) = - 28 (кВ).

Двухфазное короткое замыкание на землю.

Токи прямой, обратной и нулевой последовательности равны:

I _КА1 = 15 (кА);

I _КА2 = - I _КА1 * = - 15 * = - 6,65 (кА);

I _КА0 = - I _КА1 * = - 15 * = - 8,35 (кА);

I _КА = 0 (кА);

I _КB = m * I _КА1 = 1,5 * 15= 22,5 (кА);

I _КC = m * I _КА1 = 1,5 * 15 = 22,5 (кА).

Напряжения обратной, прямой и нулевой последовательности одинаковы и равны:

U_КА1 = U_КА2 = U_КА0 = * * U_Б2 = * * 121 = 13,37 (кВ);

U_КА = 3 * 13,37 = 40,12 (кВ);

U_КВ = U_КС = 0 (кВ).

2.3 Построение векторных диаграмм напряжения КЗ в точке М

Точка М находится за трансформатором относительно точки КЗ.

При переходе через трансформатор с нечеткой группой соединений со стороны обмотки соединений в звезду на сторону обмотки, соединенной в треугольник, векторы симметричных составляющих прямой последовательности смещаются на угол – 30º∙N; обратной последовательности – на угол +30º∙N, т.е.

= ∙ ∙ ;

= ∙ ∙ ,

где n_л –линейный коэффициент трансформации, равный отношению номинальных линейных напряжений трансформатора.

Нулевая последовательность при переходе через трансформатор не идет.