• Приближенные значения корней.

Уравнение sin х = 1 — х значительно отличается от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Рассмотрим графический способ решения уравнения.

№6.

sin х = 1 — х. В одной и той же системе координат построим два графика: график функции y = sin х и график функции у = 1— х .

Эти графики пересекаются в одной точке. Абсцисса этой точки и дает нам единственный корень нашего уравнения: х ≈ 0,5.

При х = 0,5 имеем:sin x ≈ 0,4794, 1 — х = 0,5; следовательно, sin х < 1 — х. Но тогда, как легко понять из рисунка, корень уравнения sin х = 1 —х будет больше, чем 0,5.

Проверим значение х = 0,6. Имеем:sin х ≈ 0,5446, 1— х = 0,4;следовательно, sin х > 1 — х.

Но тогда, как легко понять из того же рисунка, искомый корень x₀ должен быть меньше, чем 0,6. Теперь уже мы знаем, что x₀ находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1: x₀ ≈0,5 (с недостатком), x₀ ≈ 0,6 (с избытком).

Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы.

Ответ: ≈ 0,5.

Современная математика располагает эффективными методами приближенного решения уравнений. Эти методы излагаются в учебниках по вычислительной математике и требуют определенных знаний, которых у нас пока еще нет. Одним из таких методов-метод решения в программе Mapple. [5]

• Использование ограниченности функций и в уравнении . (Метод оценки, метод мажорант).

_{Рассмотрим применение метода на конкретных примерах.}

_№7.

.Так как при всех , тогда при любом _: при . Поэтому   х=0. При х=0 правая часть .

Ответ: 0

№8.

аrcsin (х ( х+у )) + аrcsin (у ( х+у )) = . Решение. Т.к. аrcsin t при , то левая часть уравнения не превосходит 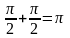.Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе: Итак, х = у, тогда получаем уравнение 2х = 1, х , у .

Ответ: ( .

№9

⁼ lg(1+ )+3х – х ² – 1. Решение. Обе части уравнения определены только для тех х, где: 4 – х² ≥ 0

4 – х² ≤ 0. Все решения системы состоят из двух чисел: х₁=2 и х₂= -2. Поэтому если уравнение имеет решения, то они могут быть только среди этих двух чисел. Проверка показывает, что число х₁ удовлетворяет уравнению, а число х₂ ему не удовлетворяет. Следовательно, уравнение имеет единственный корень х₁=2.

Ответ: 2.

• Некоторые виды уравнений, для решения которых требуется искусственный прием.

№1.

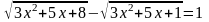_{. Пусть} тогда получаем если перемножим первое равенство со вторым следующее выражение ; . А теперь почленно сложим эти равенства. Получим , т.е. отсюда ,

Ответ:1; .

Вывод. Уравнения вида =a ( + =b) иногда рациональнее решать таким способом:

Пусть + =b ( =a ).

1) =a умножим на + =b. Тогда 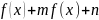=ab, где ab=m+n. 2)Сложим уравнения - =a и + =b, имеем 2 = m+n. Учитывая одз уравнения, решаем последнее уравнение. [2]

№2.

_{, можно заметить, что} . Поэтому . _{Введем замену: .} ; _{; оба корня удовлетворяют условию .}

1. _, ,

2. _{, , ,}

_Ответ:

_№3.

Уравнения, содержащие разные аркфункции

arcos x – arcsin x = arrcos x; cos (arcos x – arcsin x) = cos (arcos x);

cos (arcos x) cos (arcsin x) + sin (arcos x) sin (arcsin x) = x

x ²+ x ²= x , 2x ² = x , 2x ² - x = 0,

x (2 ² - ) = 0 ; x=0 или 2 ² = , 4–4x²=3, x²= , х

Проверка: x=0, arrcos 0–arc sin 0 = arrcos 0– верно, x=0 – корень уравнения.

х = , arrcos – arcsin = arrcos – неверно, x= – посторонний корень

x= - , arrcos (- ) arcsin (- )= arrcos (- )– неверно, x = - –не корень. Ответ: 0

Вывод. При решении уравнений, содержащих разноимённые обратные тригонометрические функции, можно пользоваться тригонометрическими тождествами.

Пусть требуется решить уравнение аrcsin f(x) = arсcos g(x). Предположим, что х - решение этого уравнения. Обозначим аrcsin f(x ) = arсcos g(x ) через α. Тогда sin α=f(x ), cos α.= g(x ), откуда f (x ) + g (x ) = 1. То, аrcsin f(x) = arсcos g(x) ; f (x) + g (x) = 1.

Аналогично получаем [4]: arctg f(x) = arctg g(x), то f(x) g(x) = 1. (По формуле tgx ctgx = 1)

№4

_sin x + cos x = . Решение. ( sin x + cos x) = , где _2=12+12.

sin x cos (/4) + cos x sin (/4) = 1, sin = 1,

x + = + 2n (n Z), x = - + 2n (n Z).

Ответ: + 2n (n Z).

Вывод.

При решении тригонометрических уравнений вида a*cos x + b*sin x = c:

1) С помощью введения вспомогательного угла: a*cos x + b*sin x = c.

Разделим обе части на = с. Легко проверить, что + = 1.

Поэтому существует такой , что cos = , sin = . Если c² a² + b², то найдётся такой угол _, что = cos . В этом случае получим уравнение, равносильное данному cos cos x + sin sin x = cos , cos(x – ) = cos .Решая это уравнение, находим множество решений x = + + , k – число целое. Если же условие c² a² + b² не выполняется, то уравнение решений не имеет.

2) Можно использовать универсальную тригонометрическую подстановку на основе формул: Если теперь ввести обозначение то .[1].

Таким образом, при решении уравнений визуально-логическим мы получили важные выводы. Все полученные выводы внесем в таблицу. (Приложение 1).