
- •Введение.
- •Цель исследования.
- •Классификация уравнений.
- •Виды уравнений
- •Однородные и сводящиеся к ним уравнения
- •Практическая часть изучения методов решения уравнений.
- •Решение однородных и сводящихся к ним уравнений
- •Приближенные значения корней.
- •Использование ограниченности функций и в уравнении . (Метод оценки, метод мажорант).
- •Некоторые виды уравнений, для решения которых требуется искусственный прием.
- •Заключение.
- •Приложение1
Решение однородных и сводящихся к ним уравнений
№1.
cos
3x
+ sin
3x
= 0. Решение.
sin
3x
= - cos
3x.
Так как значения x,
при которых cos
3x=0,
не являются корнями данного уравнения,
то разделив обе части исходного уравнения
на cos
3x,
получим уравнение, равносильное
исходному:
 =
-
=
-
 ,
или tg
3x
= - 1. Отсюда 3x
= -
,
или tg
3x
= - 1. Отсюда 3x
= -
 + n;
x
= -
+ n;
x
= -
 +
+
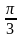 n,
n
Z.
n,
n
Z.
Ответ: - + n (n Z).
№ 2.
6 sin2 x – sin x cos x – cos2 x = 3. Решение. 6 sin2 x – sin x cos x – cos2 x – 3 (sin2 x + cos2 x) = 0. После раскрытия скобок и приведения подобных членов получаем 3sin2x - sin x cos x – 4 cos2 x = 0. Так как значения x = + n не являются корнями уравнения и cos x ≠ 0, то разделим обе части на cos2 x: 3 tg2 x – tg x – 4 = 0, tg x = - 1, x = - + n; tg x = 4/3, x = arctg (4/3) + k, n,k Z.
Ответ: - + n, arctg (4/3) + k, (n, k Z).
№3.
5x=43x . Разделив обе части на 43x и решив его, получим: x=0.
Ответ: 0.
Вывод.
Однородные показательные уравнения первой степени a f(x) =b f(x) сводятся к решению уравнения f(x) =0.
№4.
 ,
,

однородное уравнение второй степени
относительно
однородное уравнение второй степени
относительно
 и
и
 .
разделим обе части уравнения на
.
разделим обе части уравнения на
 :
:
 ;
;
 ,
,
 …
…
Ответ: ½
№5.
 +2
+2 4
4
 = 0
= 0
Решение.
ОДЗ данного уравнения x
0.
x= –корень уравнения
–корень уравнения
 =0
не является корнем данного уравнения,
то данное уравнение можно разделить на
=0
не является корнем данного уравнения,
то данное уравнение можно разделить на
 Сделав замену:
Сделав замену:
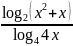 =
у получим уравнение: у3+
у2+2у-4=0,
корнем которого является только у=1.
Сделав замену:
=
у, получим
=
=
у получим уравнение: у3+
у2+2у-4=0,
корнем которого является только у=1.
Сделав замену:
=
у, получим
= .
Получим: x3+2x2+x-4=0/
.
Получим: x3+2x2+x-4=0/
Решив последнее уравнение, получим x=1. x=1-удовлетворяет ОДЗ уравнения x 0.
Ответ. x=1.
Нестандартные уравнения.
Рассмотрим некоторые встречающиеся примеры уравнений, решение которых требует эрудицию.
метод логарифмирования.
№1.
32log4
x+2=16x2.
Решение.
Область определения x
>0. Прологарифмируем обе части по
основанию 4.![]() .
Используя
свойства логарифмов, получим
.
Используя
свойства логарифмов, получим
![]()
![]()
![]()
Отметим, что x = 1/4- удовлетворяет области допустимых значений переменной x.
Ответ x = ¼
№2.
![]() Решение.
Область определения уравнения х
> 0. Так как при х > 0
обе части уравнения положительны, а
функция y
= log3
t
монотонна, то
Решение.
Область определения уравнения х
> 0. Так как при х > 0
обе части уравнения положительны, а
функция y
= log3
t
монотонна, то
![]() (1
+ log3
x)
log3
x
= 2.
(1
+ log3
x)
log3
x
= 2.
Замена: t = log3 x, tÎ R. Тогда: (1 + t) t = 2, t 2 + t – 2 = 0, t1 = –2, t2 = 1. Далее найдем x: log3 x = –2 или log3 x = 1: находим x = 1/9 или х = 3, где корни удовлетворяют одз.
Ответ. х = 1/9; х = 3.
При решении уравнения методом логарифмирования нельзя применять, если хотя бы одна из частей уравнения отрицательна, равна нулю или является суммой (разностью) выражений.
Функционально-графический метод.
Использование монотонности функций и в уравнении .
П усть
множество М
есть общая часть (пересечение) областей
существования функций f(x)
и g(х)
и пусть для любого х
є
М
справедливы неравенства f(x)≥А
и g(х)≤А,
где А – некоторое число. Тогда уравнение
f(x)
= g(х)
равносильно системе уравнений f(x)=А
усть
множество М
есть общая часть (пересечение) областей
существования функций f(x)
и g(х)
и пусть для любого х
є
М
справедливы неравенства f(x)≥А
и g(х)≤А,
где А – некоторое число. Тогда уравнение
f(x)
= g(х)
равносильно системе уравнений f(x)=А
g(х)=А. №3.
2x=3-x.
Решение. 2x=3-x.
Рассмотрим функции:
 .
Функция
.
Функция
 возрастает
на R, а функция
возрастает
на R, а функция
 убывает на R. Значит,
уравнение 2x=3-x
не может иметь на Rболее
одного корня
убывает на R. Значит,
уравнение 2x=3-x
не может иметь на Rболее
одного корня
1.Построим графики функций и .
2.Найдем
точки пересечения графиков функций:
 .
.

Как видим, графики данных функций пересекаются в одной точке (1;2). Значит, x=1.
Ответ: x=1
№4
 .
Разделим
обе части уравнения на
.
Разделим
обе части уравнения на
 .
Получим:
.
Получим:
 .
.
Функция
 убывающая
(как сумма двух убывающих функций), а
функция
убывающая
(как сумма двух убывающих функций), а
функция
 - постоянная. Уравнение не может иметь
более одного корня. Можно догадаться,
что x=1.
- постоянная. Уравнение не может иметь
более одного корня. Можно догадаться,
что x=1.
Ответ: 1
