• Однородные и сводящиеся к ним уравнения

Уравнение вида 

А(f(x))ⁿ +B(f(x))^(n-1) (g(x)) +C(f(x)) ^(n-2) (g(x))² +…+K(f(x))² (g(x)) ^(n-1) +L (g(x)) ⁿ =0

называют однородным уравнением степени n относительно f(x) и g (x).

Найдем те решения уравнения при котором g (x)=0. Затем обе части однородного уравнения разделить (g(x))ⁿ, то можно получить уравнение n-ой степени относительно ; применяя замену  =t можно   получить уравнение  A tⁿ+Bt^(n-1)+…+L=0.

• Уравнения вида

a₀ sinⁿ x+a₁ sin^{n – 1} xcos x+a₂ sin^{n – 2} xcos² x + …+ a_{n – 1}sin x cos^{n – 1}x + a_n cosⁿ x = 0, где a_0, a_{1, ... ,} a_n - действительные числа, называются однородными относительно sin x и cos x.

В этих уравнениях sinx и cosx  нулю не равны, так как не существует такого значения угла x, при котором sinx и cosx  одновременно принимали значение равное нулю. Поэтому такие уравнения решаются делением обеих частей уравнения на sinⁿx или на cosⁿx и приводятся к уравнениям отно­сительно tgx или ctgx:

a₀ tgn x+a₁ tg^{n – 1} x+a₂ tg^{n – 2} x + …+ a_n = 0, 

В основном встречаются тригонометрические и показательные однородные уравнения первой и второй степени.

• Однородное тригонометрическое уравнение первой степени:

a sin x + b cos x = 0, где a ≠ 0, b≠ 0.

• Однородное тригонометрическое уравнение второй степени:

asin²x + bsinx cosx + c cos²x = 0 где а 0, b 0, с 0.

• Однородное показательное уравнение первой степени: + =0

• _{Однородное показательное уравнение второй степени:} . [2], [3]

Примеры уравнений:

• 

• 

• 5^x=43^x

• 6 sin² x – sin x cos x – cos² x = 3.

• cos 3x + sin 3x = 0.

• +2 4 = 0

Практическая часть изучения методов решения уравнений.

• Примеры решения уравнений, сводящихся к квадратным уравнениям.

№1.

3 cos x – 10 cos x + 3 = 0.

Решение. Пусть cos x = y. Данное уравнение примет следующий вид: 3y² – 10y +3 = 0.

Решив его, найдем y₁ = 1/3, y₂ = 3. cos x = 3 не имеет решения, так как | ‌‌‌‌cos x | ≤ 1. Следовательно, cos x = 1/3; x = ± arccos (1/3) + 2n, n Z.

Ответ: ± arccos (1/3) + 2n (n Z).

 №2.

Решение. Область определения уравнения находим из условий: x+2 >0, x+2 ¹ 1; x >–2, x ¹ –1. Умножим обе части уравнения на log₅ (x+2) ¹0, получим

или, заменив log₅ (x+2) = t, придем к квадратному уравнению t ² – t – 2 = 0, t₁ = –1, t₂ =2.

Возвращаемся к первоначальной переменной:

log₅ (x+2) = –1, x+2 = 1/5, x = –9/5,

log₅ (x+2) = 2, x+2 = 25, x = 23.

Оба корня принадлежат области определения уравнения.

Ответ: x = –9/5, x = 23.

Вывод. Уравнения вида где a > 0, a ¹ 1, A, В, С – действительные числа , A¹0, В¹0, приводятся к квадратным умножением обеих частей его на log_a f(x) ¹0. Учитывая, что log_a f(x)× log_f(x) a=1 (свойство log_b a = 1/ log_a b), получим уравнение Замена log_a f(x)=t, где tÎ R приводит его к квадратному At² + Ct + B = 0. Из уравнений log_a f(x)= t₁ , log_b f(x)= t₂ найдем значения x и выберем среди них принадлежащие области определения уравнения: f(x) > 0, f(x) ¹1.

№3.

. Решение. Замена: 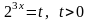_. , или , . Замена: _. , .

Ответ: 1/3.

_№4.

_. Решение. ОДЗ: . (Видимо, это уравнение приводимое к квадратным). x= -1 – не корень уравнения. Разделим на _,получим .Замена: тогда , ;

1) , , _, ( - не удовлетворяет условию одз)

2) , , , ( 8 – не удовлетворяет условию одз) Ответ: 3; -8.

№5

Решение. (Видимо, это уравнение тоже приводимое к квадратным)

Разделим обе части уравнения на x , так как x=0 не является корнем уравнения.

. Пусть , тогда , . Тогда , ,где . Имеем , ; . x=-3 не является корнем уравнения; x=5-корень.

Ответ: .