20. Ряд Тейлора и ряд Лорана.

Ряд Тейлора. Пусть функция w = f(z) аналитична в области D, z₀∈ D. Обозначим L окружность с центром в z0, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L, .

Ряд в правой части этого равенства - ряд Тейлора функции f(z). Этот ряд абсолютно сходится внутри контура L, а в качестве L можно взять любую окружность, которая не выходит за пределы области D.

Теорема о разложении функции в ряд Тейлора. Если функция w = f(z) аналитична в области D, z₀ ∈ D, то функция f(z)может быть разложена в ряд Тейлора по степеням (z – z₀)ⁿ. Этот ряд абсолютно сходится к f(z) внутри круга | z – z₀| < r, где r - расстояние от z₀ до границы области D (до ближайшей к z₀ точке, в которой функция теряет аналитичность). Это разложение единственно.

Стандартные разложения.

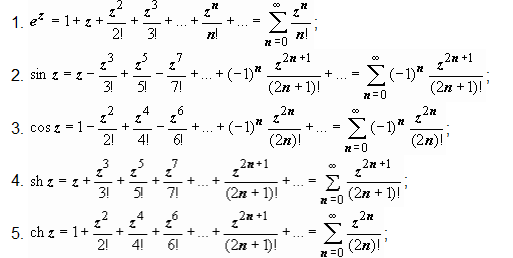
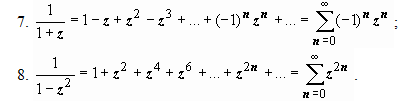
Ряд Лорана. Пусть функция f(z) аналитична в кольце ρ ≤ |z − z₀| ≤ R. Тогда для любой точки этого кольца

Этот ряд (содержащий и положительные, и отрицательные степени (z – z₀), называется рядом Лорана функции f(z). Его часть, содержащая неотрицательные степени ( ), называется правильной; часть, содержащая отрицательные степени ( ), называется главной. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.

20. Регулярные и особые точки функции. Классификация особых точек. Связь между нулем и полюсом функции.

Точка аϾС_z называется изолированной особой точкой однозначного характера функции f (z), если f (z) аналитическая и однозначная (регулярная) в кольце {z:0<|z–a|<r }, а в самой точке а не определена.

Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f (z), если f (z) регулярна в некоторой окрестности {R<|z|<∞} точки z=∞ и функция имеет в точке x =0 изолированную особую точку однозначного характера.

В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек.

Изолированная особая точка а функции f (z) называется

а) устранимой особой точкой, если существует конечный предел

б) полюсом, если

в) существенно особой точкой, если

не существует.

Типы особых точек z= функции f (z) и x =0 функции j(x) совпадают, ибо

Пусть функция f (z) регулярна в точке а (и, следовательно, в некоторой окрестности этой точки). Число m, m1, называется кратностью (или порядком) нуля функции f (z) в точке а, если выполнены условия

f(a)=f¢(a)=…=f^(m-1)(a)=0,

f^(m)(a)≠0.

При m=1 точка а называется простым нулем функции f (z), при m>1-кратным. Порядком (или кратностью) полюса функции g(z) в точке а называется кратность нуля в точке а регулярной функции

Если а – простой нуль f (z), то точка а называется простым полюсом функции g(z).

20. Вычет функции. Основная теорема о вычетах

Вычетом функции f(z) в изолированной точке z=a называется интеграл

(66)

где C - замкнутый контур, содержащий одну особую точку z=a

Основная теорема о вычетах. Если f(z) - аналитическая на границе области D и внутри области, за исключением конечного числа особых точек z1, z2, ..., zn, лежащих в D, то

(обход контура положительный).