2.3. Понятие деформации и их классификация.

Деформация – изменение формы и размеров тела под действием приложенных внешних нагрузок. Деформации могут быть разными, но всегда остается неизменным объем деформируемого тела. Объем определяется произведением трёх параметров – длины, ширины и высоты, следовательно, при любом виде деформации изменение одного из этих параметров сопровождается одновременным изменением других. Это необходимо всегда учитывать, даже если ведется речь о простых деформациях, при которых деформация вызывается одним видом сил или моментов. Общую картину можно изобразить на рисунке в пространственной прямоугольной декартовой системе координат (продольную ось всегда в сопромате выбирают с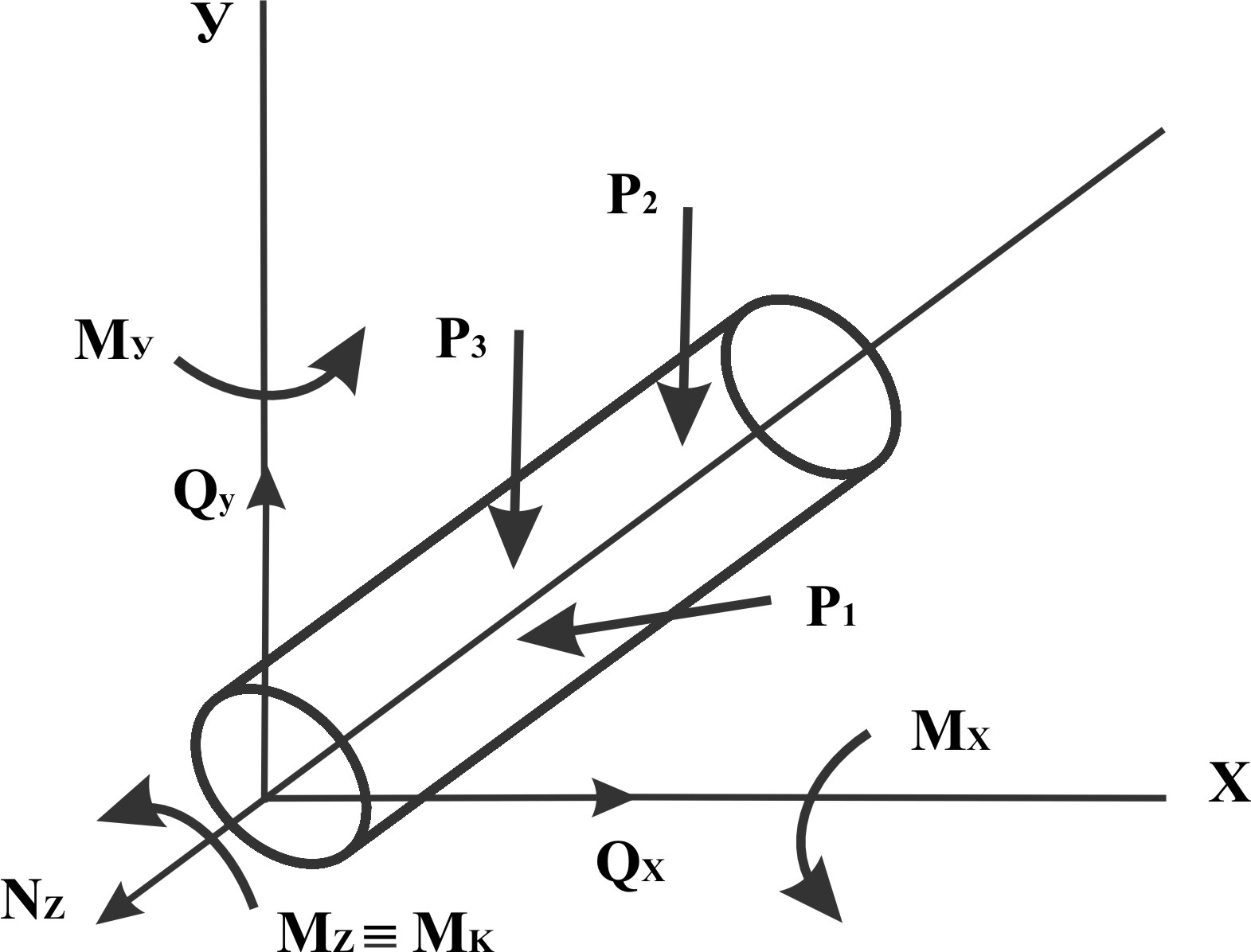 овпадающей с осью Z):

Если существует только продольная сила N - деформация растяжения или сжатия. При наличии одной только поперечной cилы Q_x или Q_y – сдвиг.

При действии только крутящего момента М_к - кручение. Действие изгибающего момента (одного) М_их или М_иу сопровождается изгибом относительно соответствующей оси.

Комбинация перечисленных вариантов приводит к сложной деформации, в которой присутствуют элементы перечисленных простых.

2.4. Закон Гука при растяжении и сжатии. Модуль Юнга.

Если к закреплённому призматическому стержню приложить нормально к торцовому сечению продольную растягивающую силу N, предварительно нанеся на поверхности сетку взаимно перпендикулярных линий, мы увидим: поперечные сечения плоские и нормальные к оси такими и останутся (это означает, что в поперечных сечениях действуют только нормальные напряжения σ = N/F равномерно распределенные по сечению); длина увеличится; поперечные размеры уменьшатся (при сжатии наоборот). Удлинение ∆l = l – l₀ называют абсолютной деформацией; отношение ∆l/l₀ = ε называют относительной деформацией (эта величина показывает на какую долю от первоначальной длины изменяется размер тела при деформировании). До определенных напряжений наблюдается линейный рост относительной деформации с ростом напряжений (это интервал упругих деформаций, которые полностью исчезают при снятии нагрузки), т.е.

ε = σ/Е; σ = Еε или ∆l/l₀ = N/EF – закон Гука при растяжении (сжатии).

Из закона Гука можно найти ∆l = Nl₀/EF или N = EF∆l/l₀ (по приложенной силе и параметрам образца определить абсолютную деформацию или по замеренной деформации и параметрам образца определить усилие, создающее деформацию).

Фигурирующий в формуле коэффициент Е для каждого материала имеет своё значение, характеризует упругие свойства материала при деформациях растяжения (сжатия), носит название модуля Юнга или модуля упругости первого рода. Его всегда можно найти в справочниках для любого материала. Физический смысл легко уяснить, если в закон Гука подставить площадь поперечного сечения равную единице и относительную деформацию взять равной единице; это даст следующий результат |E| = |N| - численное значение модуля Юнга равно продольному усилию, которое действуя на образец с площадью сечения равной единице вызовет относительную деформацию равную единице (при растяжении вызовет удлинение образца в два раза).

При продольной деформации возникает сопутствующая ей поперечная (при удлинении поперечные размеры уменьшаются).

Если ε – продольная деформация, то поперечная ε^' = - με;

μ = - ε^'/ε

называют коэффициентом поперечной деформации (коэффициентом Пуассона). Для большинства материалов он имеет значение, лежащее в интервале от нуля до 0,5 (чаще всего 0,25 ≤ μ ≤ 0,35). При расчётах пользуются ещё одним важным коэффициентом – коэффициентом запаса прочности [n] = σ_т/[σ]. При растяжении σ = N/F ≤ [σ] = σ_т/[n] (σ_т – предел текучести, [σ] – предельно допустимое напряжение). Аналогично при касательных напряжениях.