1.7. Момент силы. Главный вектор сил и главный момент системы сил.

При вращательном движении одна и та же сила оказывает разное действие (в отличие от поступательного), действие зависит от места приложения силы. Ещё Леонардо да Винчи (1452 – 1519) ввёл для описания действия силы при вращательном движении понятие момента силы М = РН, Н назвал плечом силы (плечо измеряется по перпендикуляру, проведённому из оси на направление действия силы). Момент считают положительным, если он стремится вызвать вращение против часовой стрелки, и наоборот.

Интерес представляет случай пары сил – системы двух антипараллельных сил равных по величине, лежащих в одной плоскости. Перенос пары не изменяет её момента, пары не имеют равнодействующих, момент пары можно уравновесить только парой, пара не входит ни в уравнение сил, ни в уравнение проекций сил, алгебраическая сумма моментов сил пары относительно любой точки постоянна и равна моменту пары М =Рh, где h – расстояние между силами пары по перпендикуляру к ним.

Ч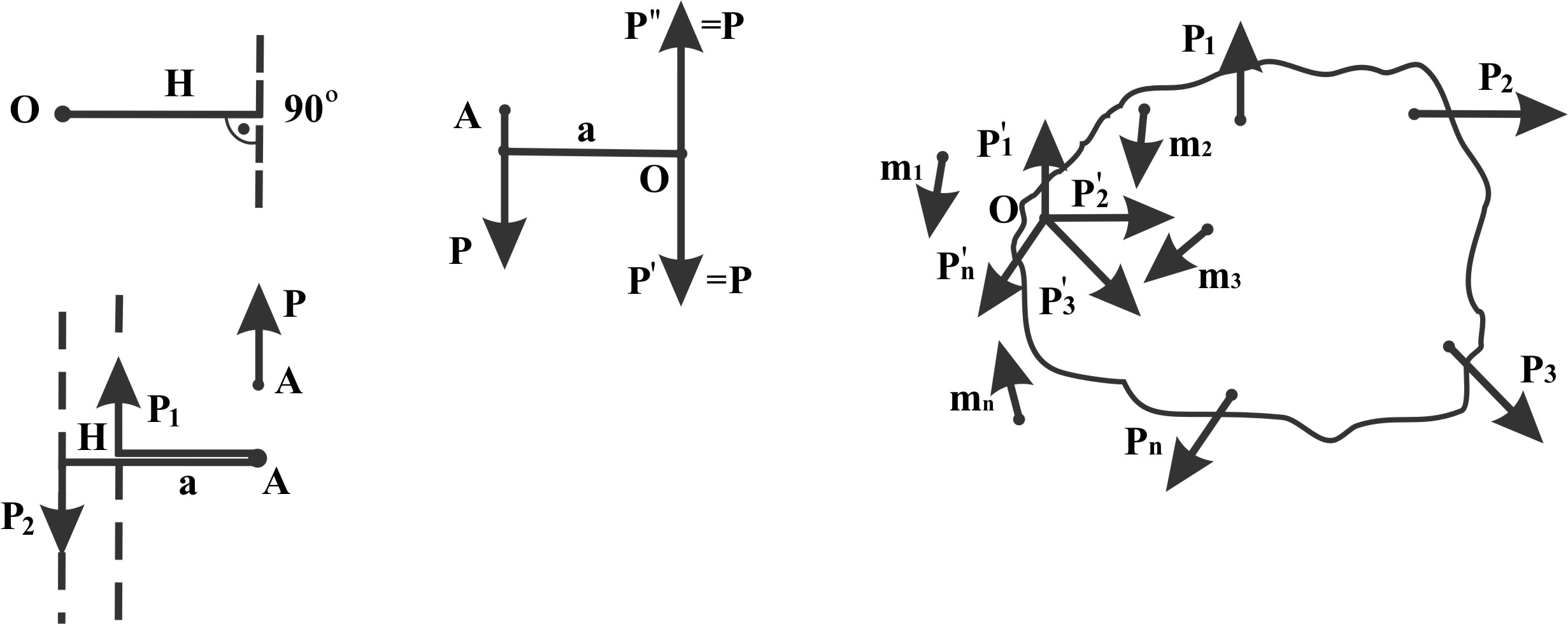 асто к твёрдому телу приложено несколько сил, действующих в одной плоскости (расположенных произвольно). Механическое состояние твёрдого тела не изменится, если любую силу перенести параллельно самой себе в любую точку тела (называемую точкой приведения или приложения), добавив при этом пару сил, момент которых равен моменту данной силы относительно новой точки приложения.

В общем случае плоская система произвольно расположенных сил эквивалентна одной силе, приложенной в точке приведения и одной паре. Эта сила называется главным вектором системы (определяют его как равнодействующую сил. перенесённых в точку приведения). Модуль главного вектора R = (R_x² + R_y²)^1/2 = ((∑X)² +(∑Y)²)^1/2. Плоская система введённых пар может быть заменена одной эквивалентной парой – главным моментом системы сил: М = m₁ + m₂ +…+m_n = ∑M₀ (P_i).

Главный вектор и главный момент плоской системы произвольно расположенных сил обладают следующими свойствами:

1. модуль и направление главного вектора системы не зависит от положения центра приведения.

2. величина и знак главного момента системы зависят от положения центра приведения (приложения), так как изменение положения центра приведения сопровождается изменением плеч сил.

3. главный вектор и равнодействующая системы сил векторно равны, но не всегда эквивалентны R^` = R = ((∑X)² + (∑Y)²)^1/2. По главному моменту и равнодействующей сил можно определить плечо равнодействующей d = M/R, которое определит положение линии действия равнодействующей.

Главный вектор и равнодействующая эквивалентны лишь при главном моменте равном нулю, что в свою очередь возможно при расположении центра приведения на линии действия равнодействующей. Сказанное позволило Вариньону (1654 - 1722) сформулировать теорему, носящую его имя, о моменте равнодействующей:

Момент равнодействующей относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраической сумме моментов составляющих сил относительно той же точки.

Возможные варианты:

1. R = 0, M = 0. Система сил такова, что тело в равновесии.

2. R ≠ 0, M ≠ 0. Модуль равнодействующей равен модулю главного вектора, параллелен ему, но направлен по другой линии.

3. R ≠ 0, M = 0. Линия действия равнодействующей проходит центр приведения и совпадает с главным вектором.

4. R = 0, M ≠ 0. Система эквивалентна паре, у которой величина и знак не зависят от положения центра приведения (одна и та же система сил не может иметь несколько эквивалентных пар).

Для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на оси координат равнялась нулю, а алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю:

∑X =0, ∑Y = 0, ∑M = 0.