21.Коэффецент запаса прочности.

Так как детали и сооружения в целом должны безопасно работать и при этих неблагоприятных условиях, то необходимо принять определенные меры предосторожности. С этой целью напряжения, обеспечивающие безотказную работу (эксплуатации) машины или любого другого сооружения, должны быть ниже тех предельных напряжений, при которых может произойти разрушение или возникнуть пластические деформации.

Таким образом, принимают σ_adm= σ_u/n_adm

где [σ]- допускаемое напряжение; [n] - нормативный (т. е. предписываемый нормами проектирования конструкций) коэффициент запаса прочности, называемый также коэффициентом безопасности, σ_u - предельное напряжение материала.

Таким образом, коэффициент запаса прочности вводится для того, чтобы обеспечить безопасную, надежную работу сооружения и отдельных его частей, несмотря на возможные неблагоприятные отклонения действительных условий их работы от расчетных.

Коэффициент запаса прочности представляют в виде произведения n=n1n2n3…

n1 - коэффициент, учитывающий неточность в определении нагрузок и напряжений.

n2 - коэффициент, учитывающий неоднородность материала.

22. Основные типы задач при расчете на прочность растянутых (сжатых) стержней.

Оценка прочности стержня. Нужно фактические напряжения в опасном сечении стержня сопоставить с допускаемыми: σ=N/A<<σ_adm называется условием прочности при растяжении (сжатии).

Пользуясь этим условием, можно решать следующие задачи:

1. Проверять прочность стержня, т. е. определять по заданным нагрузке и размерам поперечного сечения стержня фактические напряжения и сравнивать их с допускаемыми. Фактические напряжения не должны отклоняться от допускаемых более чем на ±5%. Перенапряжение больше этого значения недопустимо с точки зрения прочности, а недонапряжение свидетельствует о перерасходе материала.

2. Определять размеры поперечного сечения стержня (по известным нагрузке и допускаемому напряжению), требуемые по условию его прочности: A>>N/σ_adm

3. Определять допускаемую продольную силу по заданным размерам поперечного сечения стержня и известному допускаемому напряжению: N_adm<<A σ_adm

23. Напряжения по наклонным сечениям

где с - -р--нормальное напряжение по площадке mk, перпенди-

кулярной к растягивающей силе.

При изменении угла а меняется и величина полных напряжений р, действующих по проведённой площадке, и угол наклона их (90 - а) к этой площадке.

Для того чтобы при любом угле наклона а иметь дело всегда с одними и теми же видами напряжений, разложим напряжения на две составляющие: в плоскости тп и перпендикулярно к ней (фиг. 69). Таким образом, напряжение р, действующее в точке А ллощадки тПу мы заменяем двумя взаимно перпендикулярными напряжениями: нормальным напряже-нием Од и касательным напряжением т. Величины этих двух напряжений будут меняться в зависимости от изменения угла а между нормалью к площадке и направлением растягивающей силы.

Из фиг. 69 имеем:

о = р cos а = Go cos а, 1

(7.1)

= р sin а = Go sin а cos а = Gq sin 2а. (7.2)

Установим следующие условия относительно знаков напряжений и т. Растягивающие напряжения Од, т. е. совпадающие с направлением внешней нормали, будем считать положительными нормальные напряжения обратного направления - сжимающие - будем принимать со знаком минус.

Касательные напряжения будем считать положительными, если их направление таково, что внешняя нормаль для совмещения с ними должна повернуться по часовой стрелке. Обратное направление будем считать отрицательным. Можно руководствоваться и таким правилом знаков: если касательное напряжение т даёт момент по часовой стрелке относительно центра рассматриваемого элемента, то оно считается положительным; против часовой стрелки - отрицательным.

На фиг. 70 показаны принятые условия относительно знаков а, а и т.

При любом угле наклона площадки а

всегда будем иметь дело лишь с вумя видами напряжений, действую-*их в каждой точке проведённого Фиг. 70.

разреза: с нормальным и касательным

Напряжениями. Эти два вида напряжений соответствуют двум видам деформаций, которые испытывает материал стержня.

24. Закон парности касательных напряжений.

Сумма нормальных напряжений по двум взаимно перпендикулярным площадкам постоянна и равна главному напряжению.

На двух взаимно перпендикулярных площадках действуют равные по величине и обратные по знаку касательные напряжения.

25. напряжения действующие по любому наклонному.

Напряжения 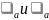в произвольном наклонном сечении можно или определить из условий равновесия трехгранной призмы АВС или вычислить по формулам

а

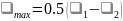
26.Определение положения главных площадок и значения главных напряжений

Если по граням выделенного элементарного параллелепипеда действуют одни только нормальные напряжения, то они называются главными напряжениями, а площадки, на которых они действуют, называются главными площадками.

для определения угла наклона главных площадок

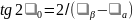
Определение главных напряжений

Определение касательных напряжений

27. Обобщенный закон Гука.

От действия одного напряжения σ₁ относительное удлинение по вертикали равно e₁₁=σ₁/E и одновременно в горизонтальном направлении сужение равно e₂₁=-vσ₁/E

Суммируя деформации получаем

e₁=σ₁/E-vσ₂/E

e₂=σ₂/E-vσ₂/E

Эти формулы выражают обобщенный закон Гука для плоского напряженного состояния.

28.Работа внешних и внутр. Сил при нагружении.

W=0,5F₁δ₁ Работа внешней статически приложенной силы равна половине произведения окончательного значения силы на окончательную величину соотв. Перемещения.

Работа внутренних сил при нагружении всегда отрицательна.

Величина равная работе внутренних сил но имеющая противоположный знак называется потенциальной энергией деформации.

U=-W­₁=N²L/2EA=EA∆l²/2L

Потенциальная энергия отнесенная к единице обьема материала называется удельной потенциальной энергией.