
Вопрос 61.
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Пусть функция y=f(x) дифференцируема на некотором отрезке [a; b]. Значение производной f'(x), вообще говоря, зависит от x, т.е. производная f'(x) представляет собой тоже функцию переменной x. Пусть эта функция также имеет производную. Дифференцируя ее, получим так называемую вторую производную от функции f(x).
Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y''или f''(x). Итак, y'' = (y')'.
Например, если
у = х5, то y'= 5x4, а y''= 20x4.
Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y'''или f'''(x).
Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n – 1)-го порядка и обозначается символом y(n) или f(n)(x): y(n) = (y(n-1))'.
Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков.
Вопрос 62. Если к графику гладкой функции в некоторой точке построить касательную, то, отложив на касательной такой отрезок, чтобы его проекция на ось Ох равнялась дельтаХ, получим в проекции на ось Оу отрезок, равный дифференциалу функции в точке касания.
Вопрос 63.
Интервалы монотонности функции.
Функция возрастает.если её производная положительна,и убывает,если производная отрицательна. 1)F'(x)=2x+1 2x+1>0=>при x>-1/2 ф-я возрастает при x<-1/2 ф-я убывает. 2)F'(x)=14x+14 14x+14>0=>при x>-1 ф-я возрастает при x<-1 ф-я убывает. 3)F'(x)=2x^2-2 2x^2-2>0;(x-1)(x+1)>0;ф-я возрастает при x<-1 и x>1 при х от -1 до 1 ф-я убывает. 4)F'(x)=-1/(3x^2) производная всегда,кроме 0,отрицательна,значит,ф-я убывает.
Экстремумы
функции
![]() .
Решение.
Данная функция определена для всех
действительных чисел, ее производная
имеет вид
.
Решение.
Данная функция определена для всех
действительных чисел, ее производная
имеет вид
 .
При этом производная не определена там,
где в нуль обращается знаменатель, т.е.
при x=0. Эта точка является критической.
Стационарных точек нет, так как в
числителе стоит постоянное число, и
потому дробь не обращается в нуль.
Учитывая, что знак производной совпадает
со знаком
.
При этом производная не определена там,
где в нуль обращается знаменатель, т.е.
при x=0. Эта точка является критической.
Стационарных точек нет, так как в
числителе стоит постоянное число, и
потому дробь не обращается в нуль.
Учитывая, что знак производной совпадает
со знаком
![]() ,
а потому и со знаком x, получаем, что
слева от x=0 (там, где x<0)
,
а потому и со знаком x, получаем, что
слева от x=0 (там, где x<0)
![]() ,
а справа
,
а справа
![]() .
Поэтому x=0 – точка минимума исходной
функции, и
.
Поэтому x=0 – точка минимума исходной
функции, и
![]() .
.
Вопрос 64.
Необходимый признак экстремума.
В точке экстремума производная функции либо
равна нулю, либо функция недифференцируема.
Но, разумеется, этот признак – не достаточный:
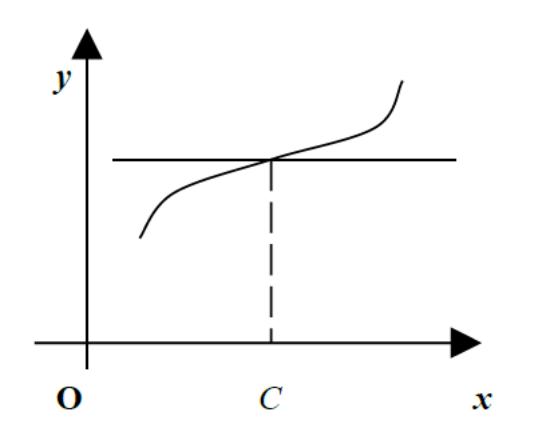
он не гарантирует того, что если в точке производная равна нулю или не существует, то эта точка будет точкой экстремума. На рисунке
f/(c)=0, но экстремума в точке x=c нет!
Условимся точки, в которых выполняется
необходимый признак экстремума называть
критическими точками функции.
Достаточные условия экстремума функции.
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех признаков экстремума, конечно, если функция удовлетворяет их условиям. Самым распространенным и удобным является первый из них.
Первое достаточное условие экстремума.
Пусть
функция y=f(x)
дифференцируема в
![]() -окрестности
точки
-окрестности
точки
![]() ,
а в самой точке
непрерывна.
,
а в самой точке
непрерывна.
Тогда
если
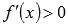 при
при
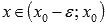 и
и
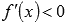 при
при
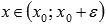 ,
то
-
точка максимума;
,
то
-
точка максимума;
если при и при , то - точка минимума.
Другими словами:
если в точке функция непрерывна и в ней производная меняет знак с плюса на минус, то - точка максимума;
если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то - точка минимума.
Алгоритм нахождения точек экстремума по первому признаку экстремума функции.
Находим область определения функции.
Находим производную функции на области определения.
Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (все перечисленные точки называют точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак).
Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).
Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак - они и являются точками экстремума.
Слишком много слов, рассмотрим лучше несколько примеров нахождения точек экстремума и экстремумов функции с помощью первого достаточного условия экстремума функции.
Второй признак экстремума функции.
Пусть
![]() ,
,
если
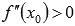 ,
то
-
точка минимума;
,
то
-
точка минимума;
если
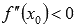 ,
то
-
точка максимума.
,
то
-
точка максимума.
Как видите, этот признак экстремума функции требует существования производной как минимум до второго порядка в точке .
Третье достаточное условие экстремума функции.
Пусть
функция y=f(x)
имеет производные до n-ого
порядка в
-окрестности
точки
и
производные до n+1-ого
порядка в самой точке
.
Пусть
![]() и
и
![]() .
.
Тогда,
если n – четное, то - точка перегиба;
если n – нечетное, то - точка экстремума, причем
если
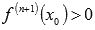 ,
то
-
точка минимума;
,
то
-
точка минимума;
если
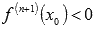 ,
то
-
точка максимума.
,
то
-
точка максимума.
