Вопрос 58.

Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• аркси́нус (обозначение: arcsin)

• аркко́синус (обозначение: arccos)

• аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)

• арккота́нгенс (обозначение: arcctg; в иностранной литературе arccotan)

• арксе́канс (обозначение: arcsec)

• арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin⁻¹ для арксинуса и т.п.; это считается неоправданным, так как возможна путаница с возведением функции в степень −1

Производные обратных тригонометрических функций:

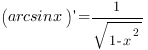
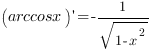
Вопрос 59.

Производная логарифмической функции для любого х из области определения находится по формуле

(1)

По основному логарифмическому тождеству х = е^{ln х} при всех положительных х, т. е. в этом равенстве справа и слева стоит одна и та же функция (определенная на R₊). Поэтому производные х и е^{ln x} равны, т. е.

x' = (e^{ln x})' (2)

Известно, что х' = 1. Производную правой части вычисляем по правилу нахождения производной сложной функции и теореме 1 : (е^{ln x})'= е^{ln х} ln' x=x ln' x. Подставляя найденные производные в равенство (2), находим l = х ln' х, откуда .

Вопрос 60.

Производная степенно-показательной функции

Данную функцию мы еще не рассматривали. Степенно-показательная функция – это  функция, у которой и степень и основание зависят от «икс». Классический пример, который вам приведут в любом учебнике или на любой лекции:

Как найти производную от степенно-показательной функции?

Необходимо использовать только что рассмотренный приём – логарифмическую производную. Навешиваем логарифмы на обе части:

Как правило, в правой части из-под логарифма выносится степень:

В результате в правой части у нас получилось произведение двух функций, которое будет дифференцироваться по стандартной формуле .

Находим производную, для этого заключаем обе части под штрихи:

Дальнейшие действия несложны:

Окончательно:

Если какое-то преобразование не совсем понятно, пожалуйста, внимательно перечитайте объяснения Примера №11.

В практических заданиях степенно-показательная функция всегда будет сложнее, чем рассмотренный лекционный пример.

Логарифмическое дифференцирование

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:

Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.

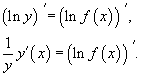
Отсюда видно, что искомая производная равна