3. Визначення розрахункових граничних моментів внутрішніх зусиль

За критерій вичерпання несучої здатності перерізу, що обумовлює втрату рівноваги між зовнішніми і внутрішніми зусиллями, розрахунковий граничний момент можна визначити як максимальний на діаграмі “момент - кривизна” (екстремальний критерій). Таку задачу можна вирішувати теоретичним і практичним шляхами. За теоретичним шляхом необхідно записати рівняння згинальних моментів як функцію кривизни і вирішити рівняння відносно згинального моменту. Практичним шляхом можна побудувати графік залежності між моментами і кривизною і на ньому знайти максимальне значення моменту або використати максимальне значення коефіцієнта для задоєного класу бетону (табл. Б.3 додатку Б).

Графік залежності “момент - кривизна” можна побудувати наступним чином. Задаючись з певним кроком зміною деформацій стиснутого бетону , знаходяться відповідні значення деформацій в розтягнутій арматурі та відповідні значення згинального моменту М за формулою (16). Кривизна елемента знаходиться за формулою

. (23)

Деформації стиснутого бетону необхідно змінювати від до , на приклад через . За знайденими М і χ будується графік, на якому визначається графічно момент (рис. 4).

Можна також з метою повного використання в роботі

4. Практичний метод розв’язання рівняння рівноваги.

В рівняннях рівноваги (16) і (17) при заданому значенні деформації в бетоні невідомою є висота стиснутої зони бетону . Практично задача знаходження невідомого вирішується методом наближень з заданою точністю . Наприклад, точність визначення висоти стиснутої зони бетону можна прийняти 2 або 5%.

На першому кроці наближення при значенні можна прийняти і перевірити рівняння (17), позначивши ліву частину рівняння , а праву . Якщо

, (24)

то на другому кроці наближення уточнюється значення , прийнявши , де - крок наближення ( можна прийняти 0,1 або 0,05).

При значенні знову перевіряється умова (17). Якщо вона не виконується, робиться третій крок наближення. Такі наближення повторюються до задоволення умови (17).

За знайденим в останньому наближенні знаходиться згинальний момент за формулою (16).

5. Розрахунок несучої здатності поперечних перерізів згинальних залізобетонних елементів з одиничною арматурою

Суть розрахунку зводиться до визначення площі поперечного перерізу розтягнутої арматури , а арматура в стиснутій зоні відсутня (рис. 2). Методика визначення площі арматури в ДСТУ Б В.2.6-156:2010 не наводиться.

Для елементів з одиничною арматурою формули (16) і (17) можна записати у вигляді:

;

(25)

, (21)

де - розрахунковий граничний момент від зовнішнього

навантаження;

- деформації в розтягнутій арматурі, які визначаються за формулою (5).

За критерій вичерпання несучої здатності можна прийняти руйнування стиснутого бетону при досяганні фібровими деформаціями граничного значення . В подальшому задачу можна розв’язати методом наближень. На першому кроці приймається значення , після чого за формулою (5) знаходиться значення , а площа розтягнутої арматури знаходиться з рівняння (21)

, (22)

при цьому не повинна перевищувати , щоб не було розриву арматури.

Після визначення граничний розрахунковий момент внутрішніх зусиль можна визначити за формулою

. (23)

Якщо виявиться, що

, (24)

розв’язок задачі знайдено. Якщо умова (24) не виконується необхідно на другому кроці змінити висоту стиснутої зони і розрахунок повторити. Розрахунок повторюється до досягання виконання умови (24), за якою кінцево приймається площа поздовжньої розтягнутої арматури .

Якщо виявиться, що за будь яких значень , необхідно встановити арматуру в стиснутій зоні.

Приклад 1. Визначити несучу здатність поперечного перерізу згинального елементу за таких даних: матеріал – бетон класу С20/25, арматура класу А400С; розміри поперечного перерізу = 50см; = 20см; = 3см; = 5см; арматура в стиснутій зоні 2Ø12А400С, в розтягнутій зоні − 2Ø25А400С (рис. 5).

Дано: f_cd = 14,5 МПа = 1,45 кН/см²; d = h – a₂ = 45 см; а1 = 2,8785; а2 = -3,1586; а3 = 1,7454; а4 = -0,52904; а5 = 0,06374; ε_с1 = 0,00165; ε_сu1 = 0,00344; A_s1 = 2,26 см²; A_s2 = 9,82 см²; E_s = 210 000 МПа = 21 000 кН/см².

Результати визначення моментів внутрішніх зусиль в поперечному перерізі згинального елементу при різних значеннях відносної деформації бетону в крайніх волокнах, виконаного методом послідовних наближень в програмному середовищі Excel представимо в табличній формі (табл. 1), а залежність значення моментів від кривизни представимо на діаграмі (рис. 6).

Таблиця 1

Результати визначення моментів внутрішніх зусиль в поперечному перерізі згинального елементу

εс / εсu1	z / d	χ, ×10-5 см-1	M, кН·см
0		0	0
0,1	0,315	2,43	7770
0,2	0,332	4,61	14285
0,3	0,35	6,55	19665
0,4	0,367	8,33	24195
0,5	0,384	9,95	27956
0,6	0,401	11,44	31057
0,7	0,417	12,83	33693
0,8	0,433	14,12	35834
0,9	0,450	15,29	37407
1,0	0,466	16,40	38679
1,1	0,483	17,41	39440
1,2	0,501	18,31	39711
1,3	0,519	19,15	39651
1,4	0,537	19,93	39318
1,5	0,555	20,66	38806
1,6	0,572	21,38	38384

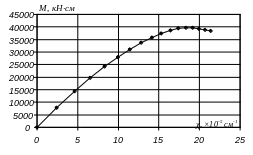
Рис. 6. Залежність моментів внутрішніх зусиль від кривизни.

Отже, максимум на діаграмі буде визначати несучу здатність згинального елемента:

М_su = 39 711 кН·см = 397,11 кН·м.

Приклад 2. Визначити площу поперечного перерізу розтягнутої арматури в балці за таких даних: = 600 кНм; = 60см; = 25см; клас бетону С25/30; арматура класу А400С; = 5см.

Рішення:

1. Механічні і деформаційні характеристики бетону - = 17,0 МПа; = 2,6 МПа; = 29000 МПа; = 355*10^-5; коефіцієнти діаграми деформування бетону - = 2,518; = -2,0904; = 0,6077; =-0,01675; =-0.01855 ( з таблиць ДБН В.2.6 – 98: 2009), механічні і деформаційні характеристики арматури - = 400МПа; = 2,1*10⁵ МПа; = 0,025 ( з таблиць ДСТУ Б В.2.6 – 156: 2010).

2. За критерій вичерпання несучої здатності приймається руйнування стиснутого бетону при досягненні деформацій граничного значення .

3.Для бетону С25/30 максимальне значення повноти епюри буде:

( див табл. )

4. На першому кроці приймається значення =0,275 м.

5. За формулою (5) знаходимо значення

= =

=202,9*10^-5 < 0,025

6. Знаходимо площу розтягнутої арматури

=

*

=0,002212м² = 22,12см²

6. Граничний розрахунковий момент внутрішніх зусиль визначаємо за формулою

=

=771,56кНм

6. Перевіряємо умову

22,23% > 5%

Умова не виконується, тому зменшуємо висоту стиснутої зони до задовільного виконання умови.

7. Умова буде виконуватися при висоту стиснутої зони = 0,21м

і перераховуємо п. 3 – 6.

8. За формулою (5) знаходимо значення

= =328,5*10⁵

9. Знаходимо площу розтягнутої арматури

=

*

=0,001043м² = 10,43см²

10. Граничний розрахунковий момент внутрішніх зусиль визначаємо за формулою

=

=613,63кНм

6. Перевіряємо умову

2,22% < 5%

Умова виконується

Приймаємо 2 Ø 28 А400С ( А_s = 12,22 см²)

( блок схема A_s2)

1. ДБН В.2.6-98:2009. Бетонні та залізобетонні конструкції. Основні положення. – Київ: Мінрегіонбуд України, 2011. – 71с.

2. ДСТУ Б В.2.6-156:2010. Бетонні та залізобетонні конструкції з важкого бетону. Правила проектування. – Київ: Міністерство регіонального розвитку та будівництва України, 2010. – 166 с.

3. Бабич Є.М Розрахунок нерозрізних залізобетонних балок із використанням деформаційної моделі: Рекомендації / Бабич Є.М., Бабич В.Є., Савицький В.В. – Рівне: НУВГП, 2005. – 38 с.