Вариант 3: Использование вычислительного блока Given - Find

Вычислительный блок используется следующим образом:

С клавиатуры вводится ключевое слово Given (Дано), за ним уравнение или система уравнений, причем равенства должны быть тождественными (<CTRL>+<=>), затем с клавиатуры вводится Find (Найти ), за ним указывается неизвестный (неизвестные в скобках) и добавляется оператор ▌ → (можно щелчком ЛКМ по одноименной кнопке палитры Символические операторы либо воспользоваться комбинацией (<CTRL>+<.>). Результаты вычислений появляются после щелчка ЛКМ вне последнего блока.

Пример 1

Найти корни уравнения

Решение:

Given

Find (x) →(0 ½)

Пример 2

Решить систему уравнений

Решение:

Given

Find (x, y) →

5. Построение графиков функций

Mathcad обладает огромными возможностями по графическому представлению данных. Рассмотрим возможности построения графиков функций одной переменной. Для построения графика функции необходимы следующие действия:

• определить функцию пользователя;

• задать диапазон изменения аргумента (используя переменную индекса);

• вставить в документ шаблон - заготовку будущего графика (можно воспользоваться либо клавишей {@}, либо комбинацией клавиш {SHIFT}+2, либо нужной кнопкой из палитры Графики);

• заполнить пустые поля заготовки.

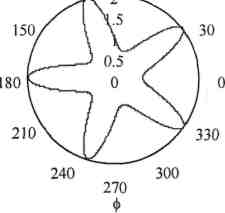
Пример1: Построить график функции на участке изменения х [0,4] Решение: х:=0,0.5..4 f(x):=x2	Пример 2: Построить график в полярных координатах Решение:
x

Можно на одной заготовке построить несколько графиков. Для этого необходимо указывать имена функций и аргументов через запятую.

Пример1:

Построить графики функций и на участке изменения х [0,4] и t [0,4]

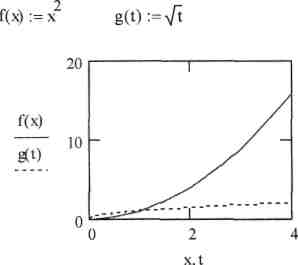
Решение:

х:=0,0.5..4 t:=0,0.5..4

^f(x):=x2

6. Математический анализ

Основным действиям математического анализа в программе Mathcad отведена палитра Calculus (Операторы математического анализа). С ее помощью можно вычислять пределы функций, производные 1 - ого и производные высших порядков, неопределенные и определенные интегралы, суммы числовых и степенных рядов, произведения.

Вычисление производных 1-ого порядка

На листовое поле вводится шаблон из палитры Calculus, щелчком по кнопке инструментов . Позиции (знакоместа) заполняются обычным образом.

Пример 1.

Найти производную функции у(х) .

Решение:

.

Пример 2.

Найти производную функции

Решение:

Simplify -(выбираем из палитры Символьно) позволяет упрощать выражения.

Вычисление интегралов

Неопределенные интегралы вычисляются с помощью кнопки , щелчком ЛКМ, по которой вставляется на листовое поле шаблон из палитры .

Позиции (знакоместа) заполняются обычным образом

Пример 1.

Вычислить неопределенный интеграл

Решение:

Пример 2.

Вычислить неопределенный интеграл

Решение: Для получения компактных результатов нахождение неопределенных интегралов следует дополнять командой символьного преобразования (заполненного шаблона), в данном примере командой simplify.

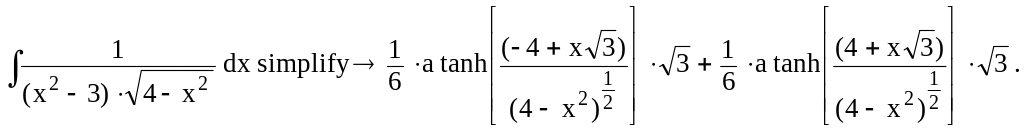
Если не воспользоваться командой simplify , то полученное выражение будет очень громоздким, хотя и не ошибочным. Предлагается проверить самостоятельно.

Определенные интегралы вычисляются аналогичным образом с помощью шаблона из палитры . Точные результаты вычислений выводятся командой Вычислить Символьно (■→), а приближенные - клавишей «=».

Пример 1.

Вычислить площадь фигуры, ограниченной линиями y=cos⁵(x)* sin(2x), у=0, 0 < х < /2.

Решение:

Вводим заданную функцию (как функцию пользователя) на листовое поле. Строим график функции, создавая фигуру, площадь которой надо вычислить (сразу задаем граничные значения промежутка изменения х).

у(х) := cos(x)⁵•sin(2•х)

По графику задаём границы области интегрирования, заполняя знакоместа в шаблоне:

х

10