- •Самостоятельная работа Изучение пакета математического моделирования mathcad
- •1. Основные преимущества системы mathcad
- •2. Пользовательский интерфейс
- •3. Элементы, используемые при составлении mcad ‑ документов
- •3.1. Переменные
- •Как напечатать греческие буквы
- •Предопределенные переменные
- •3.2. Операторы
- •3.3. Функции
- •4. Решение уравнений и их систем
- •Вариант 3: Использование вычислительного блока Given - Find
- •5. Построение графиков функций
- •6. Математический анализ
3.3. Функции
Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. Функции принимают набор параметров и возвращают значение (скалярное или матричное). В формулах можно использовать стандартные встроенные функции, а также функции, определенные пользователем.
Чтобы использовать функцию в выражении, надо определить значения входных параметров в скобках после имени функции. Имена простейших математических функций (sin(x), cos(x), tg(x), log(x),ex) можно ввести с панели (палитры) Калькулятор. Имена других встроенных функций можно узнать (выбрать) из диалогового окна Вставить функцию, которое появляется после щелчка ЛКМ по кнопке f(x).
Примеры использования некоторых встроенных функций:
1. Самостоятельный вызов функции sin() = 0.
Использование функции в вычислении переменных a: = mod(15,4) а = 3.
Вызов функции внутри некоторого выражения a: =4.mod(10,3) а = 4.
Функции, определенные пользователем* используются таким же образом, как и стандартные (либо как самостоятельная функция, либо в вычисляемом выражении, либо внутри другой функции).
Но, прежде чем использовать пользовательскую функцию её необходимо определить.
Для определения функции пользователю необходимо:
ввести имя функции, (по правилам для определения имен переменных),
далее, в круглых скобках указать через запятую список формальных параметров (формальные параметры - это переменные, от которых зависит функция),
далее ввести оператор присваивания и записать выражение, определяющее саму функцию. В выражении могут использоваться математические действия, математические символы, константы, переменные из списка формальных параметров, вызовы встроенных и определенных ранее функций, а также имена переменных определенных ранее.
Пример:
|
определили функцию пользователя по переводу градусов в радианы. (Примечание. Набирайте формулу с помощью калькулятора.) |
Rad(180) = 3,14 |
использование функции Rad. |
Sin(Rad(30)) = 0,5 |
использование функции Rad.
|
Последовательность целочисленных значений i = m…n (с единичным шагом) задаётся следующим образом
<i>< <shift> <:>><m><;> <n>
На листовом поле будет выглядеть i:= m..n, причем точек между начальным и конечным значением - две.
Для выполнения повторяющегося (многократного) вычисления в Mathcad следует сделать следующие шаги:
Шаг 1: задать функцию (по правилу определения функции)
Шаг 2: задать интервал изменения аргумента (последовательность целочисленных значений i = m…n)
Шаг 3: На листовом поле ввести имя функции с переменной и набрать знак вычислить(=)
Пример:
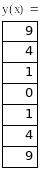
Вычислите
х2
для
![]() .
.
![]()
![]()
4. Решение уравнений и их систем
Для решения уравнений, а также систем уравнений (алгебраических, иррациональных, показательных, логарифмических) в Mathcad существует много возможностей: использование различных встроенных функций, символьных вычислений, аналитических вычислений, вычислительного блока решений и прочие. Рассмотрим некоторые варианты.
Вариант 1: Использование функции root
Функция root служит для решения уравнений вида f(x)=0, где f(x)- выражение, корни которого нужно найти, а х- неизвестное. Для поиска корней с помощью функции root достаточно вызвать функцию root(f(x),x) и правильно вписать в означенные поля (знакоместа) параметры.
Пример 1:
Найти
корни уравнения ![]()
Р
=
Прежде всего необходимо присвоить произвольное значение переменной t, например:
t=2.
![]()
Пример 2:
Найти корни уравнения 2 • sin(x) - х = 0.
Решение:
x=1.
![]()
Вариант 2: Использование оператора solve
Оператор solve выбираем из палитры Символические операторы и щелчком ЛКМ помещаем его шаблон на листовое поле: ▌solve, ▌ →
В левую отмеченную позицию помещаем уравнение, набирая знак «=»как комбинацию клавиш <CTRL> + <=>, а в правую помещаем неизвестную величину.
Пример 1:
Найти
корни уравнения ![]()
Решение:


Пример 2:
Найти
корни уравнения ![]()
Решение:
![]()
Пример 3:
Решить
систему уравнений
![]()
Решение:
![]()
Для заполнения левой позиции (знакоместа) в подобных задачах систему уравнений «вписываем» в вектор из n - строк (n - количество уравнений) и одного столбца, и в правую позицию аналогично помещаем вектор - столбец из n переменных величин.