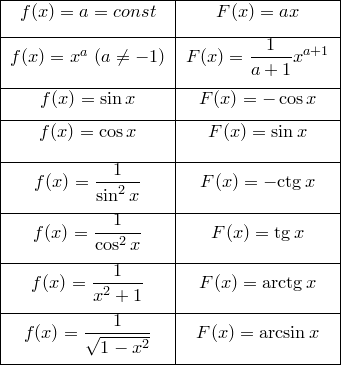1. ОКРЕСТНОСТЬ. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКЕ И БЕСКОНЕЧНОСТИ. ОДНОСТОРОННИЕ ПРЕДЕЛЫ.
2. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ, ИХ СВОЙСТВА. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИИ. ЕДИНСТВЕННОСТЬ ПРЕДЕЛА.
Бесконечно малые
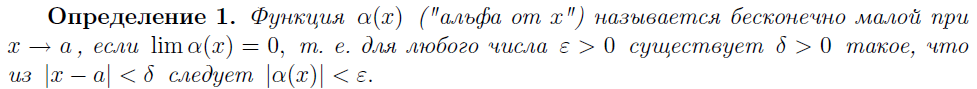
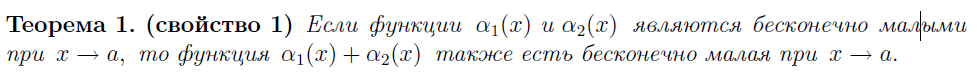
Бесконечно большие
Основные теоремы
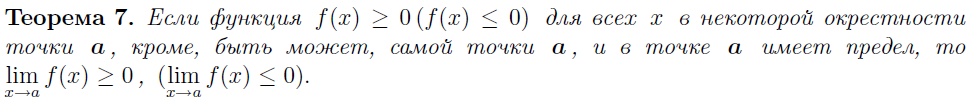
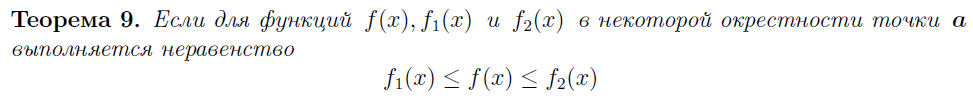
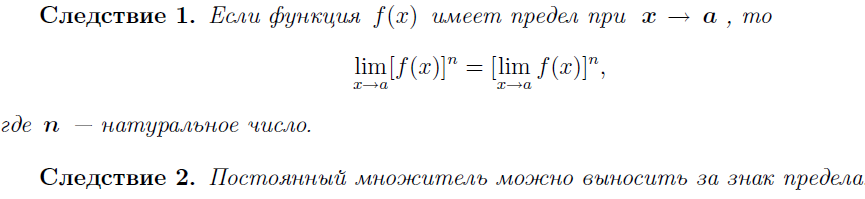
Теорема. Если функция или последовательность имеет предел, то он единственен.
3. ОСОБЫЕ СЛУЧАИ ПРЕДЕЛОВ СУММЫ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО. НЕОПРЕДЕЛЕННОСТИ. СПОСОБЫ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ. ПРИМЕРЫ.
Непосредственная подстановка:
Разложение на множители:
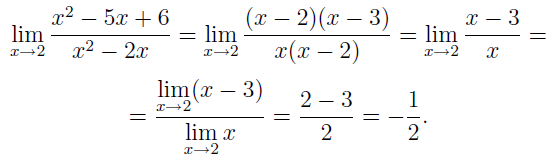
Умножение на сопряженное:
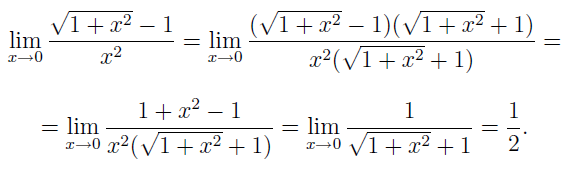
Почленное деление числителя и знаменателя на степень многочлена в знаменателе
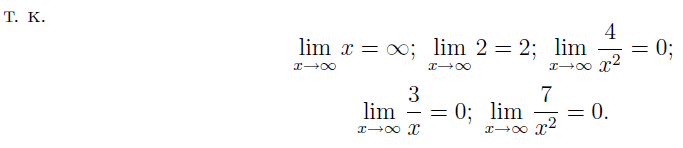
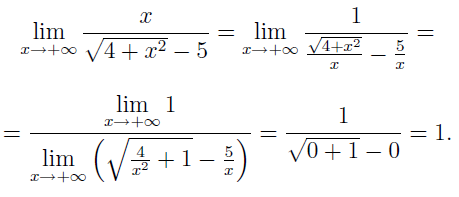
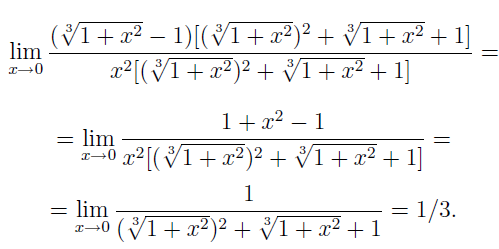
4. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И СЛЕДСТВИЕ ИЗ НЕГО. ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И СЛЕДСТВИЯ. СРАВНЕНИЯ БЕСКОНЕЧНО МАЛЫХ. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ. ЗАМЕНА БЕСКОНЕЧНО МАЛЫХ ИХ ЭКВИВАЛЕНТНЫМИ ПРИ ВЫЧИСЛЕНИИ ПРЕДЕЛОВ.
Первый
замечательный предел:
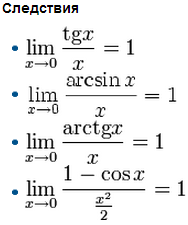
Второй замечательный
предел
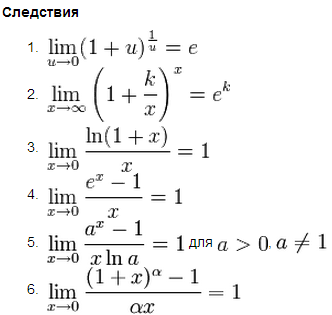
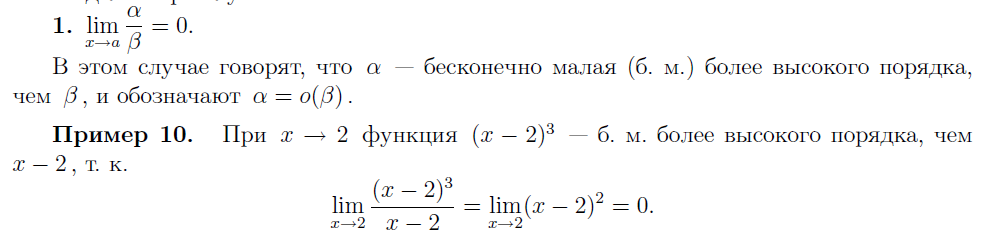
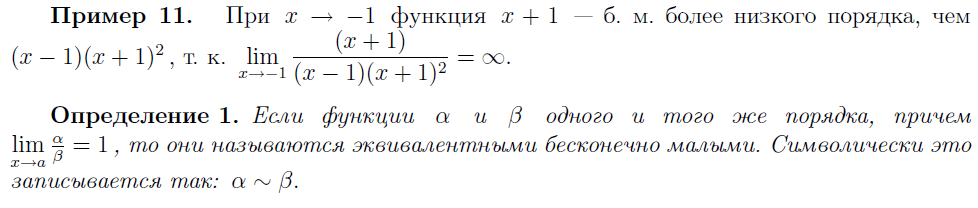
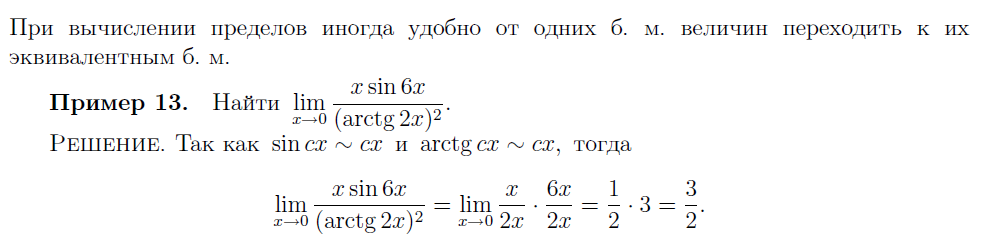
5. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ, НЕПРЕРЫВНОСТЬ В ТОЧКЕ СЛЕВА И СПРАВА. ОСНОВНЫЕ ТЕОРЕМЫ О НЕПРЕРЫВНЫХ ФУНКЦИЯХ.
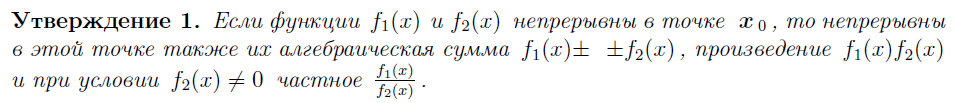
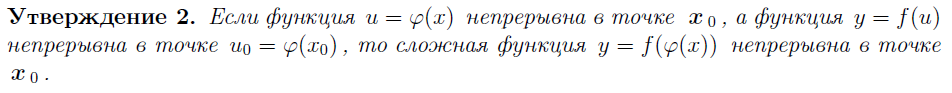
6.
ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ.
7. ФУНКЦИИ, НЕПРЕРЫВНЫЕ НА ОТРЕЗКЕ. СВОЙСТВА ФУНКЦИЙ НА ОТРЕЗКЕ (ТЕОРЕМЫ ВЕЙЕРШТРАССА И БОЛЬЦАНО - КОШИ).
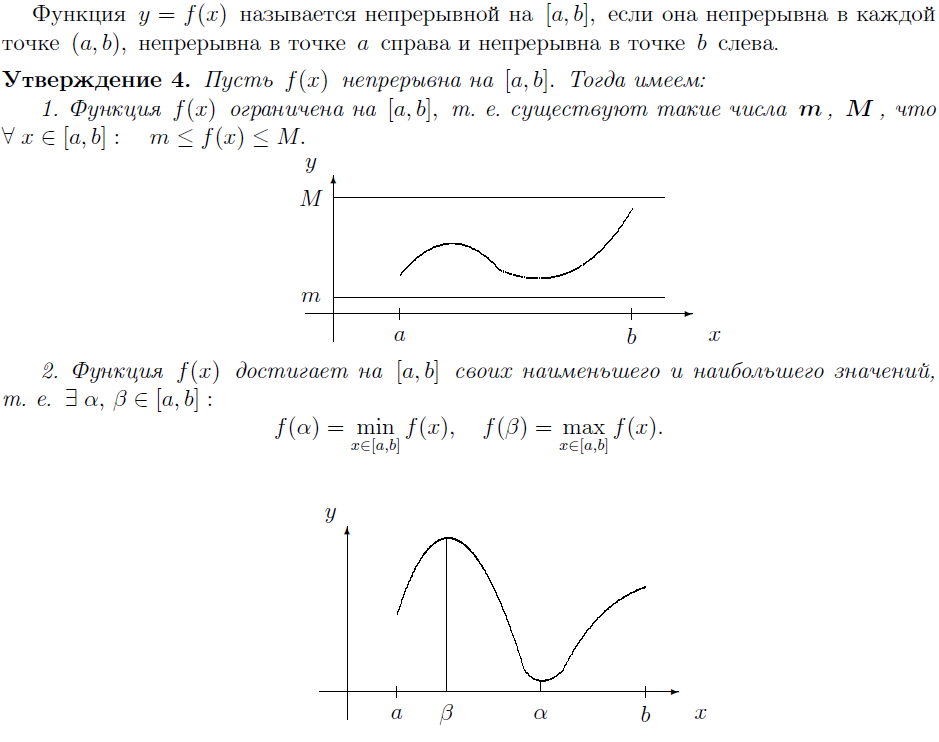
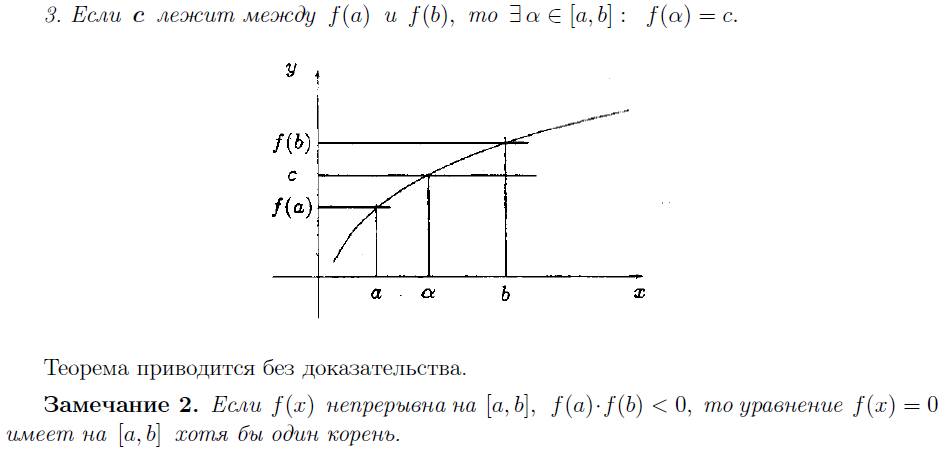
Теорема Вейерштрасса: если функция непрерывна на отрезке, то она ограничена на нем.
Теорема Больцано-Коши: если функция может принимать два значения, то она может принимать и любое значение между ними.
8. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ ПРОИЗВОДНЫЕ. ОДНОСТОРОННИЕ ПРОИЗВОДНЫЕ, ИХ СВЯЗЬ С ПРОИЗВОДНОЙ. МЕХАНИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ.
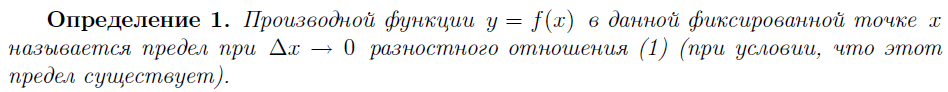
Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.
Геометрический
смысл производной: Производная
функции
в точке
равна тангенсу угла, образованного
касательной к графику функции в этой
точке и положительным направлением оси
:
,
где
- угол между касательной к графику
функции в точке
и положительным направлением оси
.
Физический
смысл:
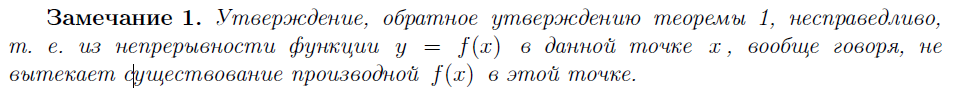
9. ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ. НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ ДИФФЕРЕНЦИРУЕМОСТИ. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ФУНКЦИЙ. ДИФФЕРЕНЦИРОВАНИЕ ОБРАТНОЙ ФУНКЦИИ. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ.
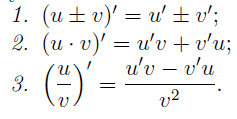
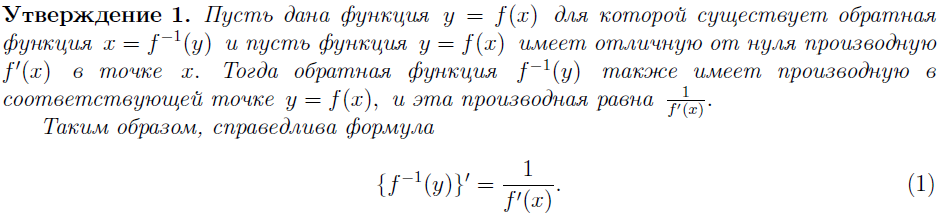
10. Производные функций: Правила дифференцирования 11. Производные тригонометрических функций.
12. ПРОИЗВОДНЫЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
|
|
13. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ. ПРОИЗВОДНАЯ СТЕПЕННО-ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ.
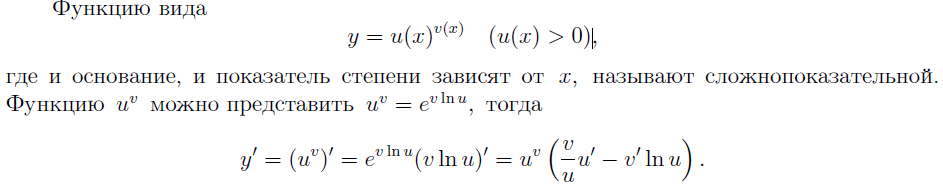
14. ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИИ И НЕЯВНО.
Параметрически
Неявно
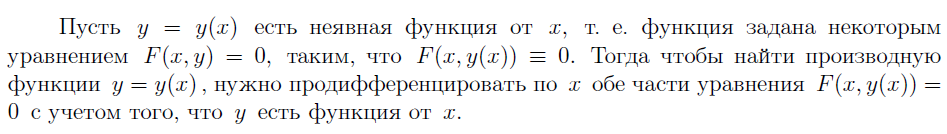
15. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ ВТОРОГО ПОРЯДКА. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ И НЕЯВНО.
16. Уравнение касательной и нормали к кривой. § Уравнения касательной и нормали к графику функции
Определение касательной к графику функции |
Касательной
к графику функции в точке
|
называют предельное положение секущей,
соединяющей точки
и
графика, при стремлении точки
к точке
по графику.
Геометрический смысл производной |
Производная функции в точке равна тангенсу угла, образованного касательной к графику функции в этой точке и положительным направлением оси : , где - угол между касательной к графику функции в точке и положительным направлением оси . |
Уравнение касательной |
Пусть функция в точке имеет производную . Тогда в точке существует касательная к графику этой функции, уравнение которой:
|
.
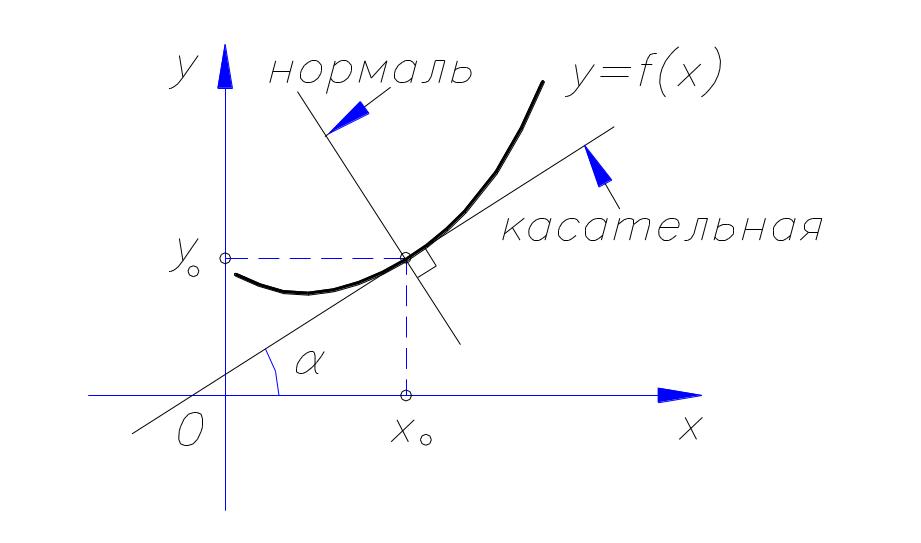
Определение нормали |
Прямая
линия, проходящая через точку касания,
перпендикулярно касательной, называется
нормалью к кривой.
Уравнение нормали:
Пусть функция
в точке
имеет производную
.
Тогда в точке
существует нормаль к графику этой
функции, уравнение которой: Если
|
.
(то есть касательная горизонтальна),
то нормаль вертикальна и имеет уравнение
.17. ДИФФЕРЕНЦИАЛ И ЕГО СВЯЗЬ С ПРОИЗВОДНОЙ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ.
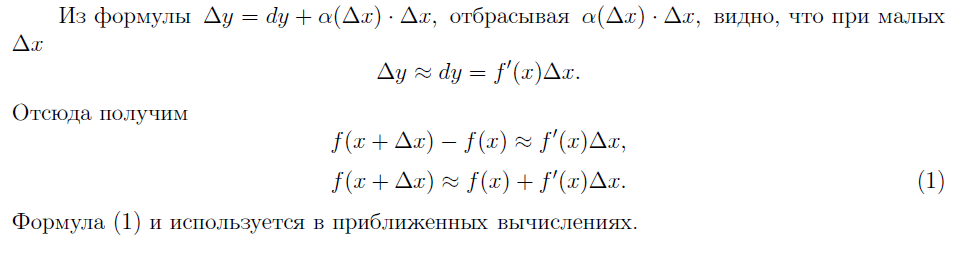
18. ДИФФЕРЕНЦИАЛ СЛОЖНОЙ ФУНКЦИИ. ИНВАРИАНТНАЯ ФОРМА ДИФФЕРЕНЦИАЛА. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. НАРУШЕНИЕ ИНВАРИАНТНОЙ ФОРМЫ ЗАПИСИ ДИФФЕРЕНЦИАЛОВ ВЫСШИХ ПОРЯДКОВ.
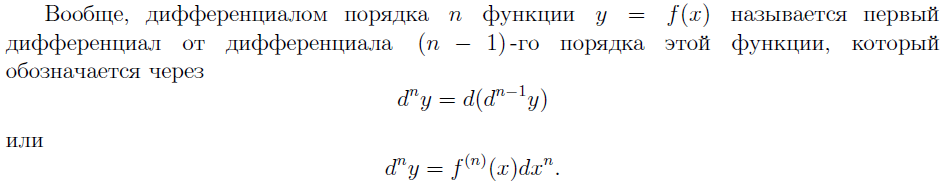
19. ТЕОРЕМА ФЕРМА И РОЛЛЯ, ИХ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.
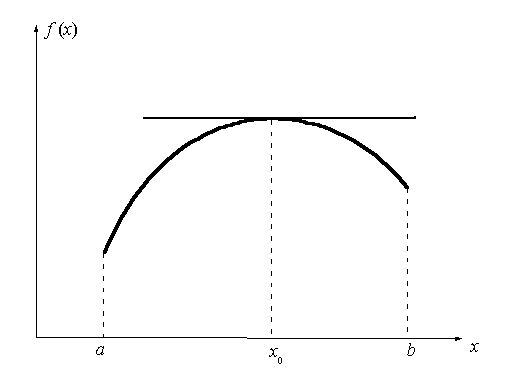
Геометрический смысл теоремы состоит в том, что в точке экстремума касательная к кривой параллельна оси абсцисс
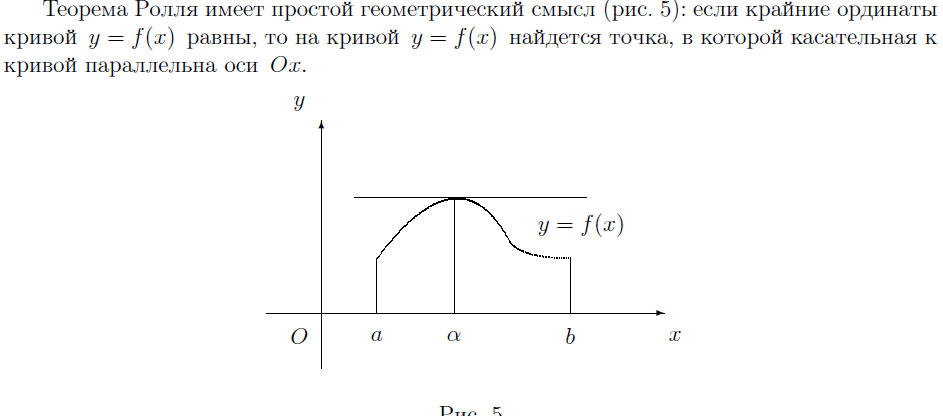
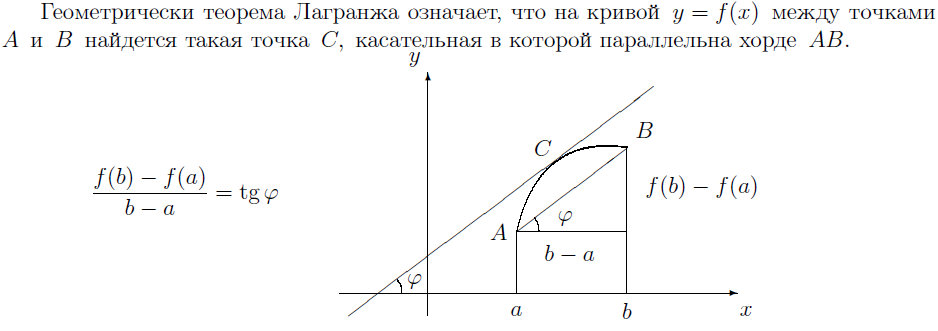
20. ТЕОРЕМА ЛАГРАНЖА, ЕЕ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ТЕОРЕМА КОШИ.
21. ПРАВИЛО ЛОПИТАЛЯ.
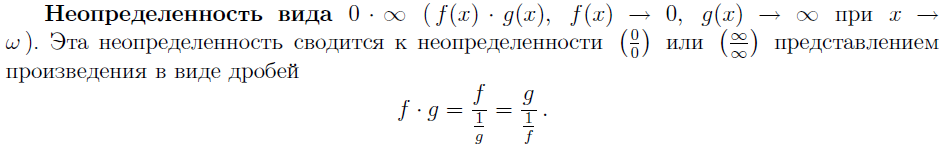
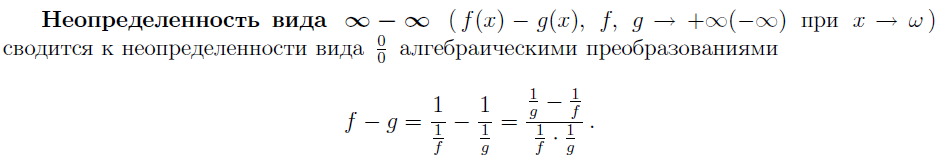
22. УСЛОВИЕ ПОСТОЯНСТВА ФУНКЦИИ. УСЛОВИЯ МОНОТОННОСТИ ФУНКЦИИ.
Условие постоянства
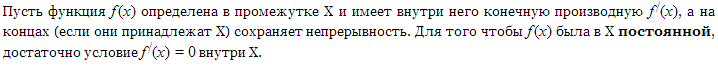
Условие монотонности
23.
ПОНЯТИЕ МАКСИМУМА И МИНИМУМА ФУНКЦИИ.
НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМА.
ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА (ПО
ПЕРВОЙ ПРОИЗВОДНОЙ). ДОСТАТОЧНОЕ УСЛОВИЕ
ЭКСТРЕМУМА (ПО ВТОРОЙ ПРОИЗВОДНОЙ).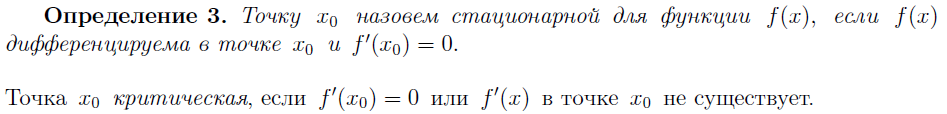 
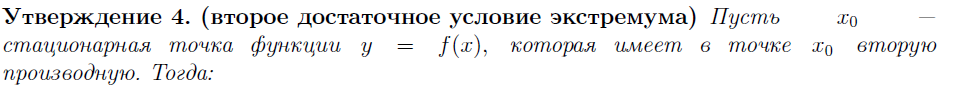
24. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ И ИХ НАХОЖДЕНИЕ.
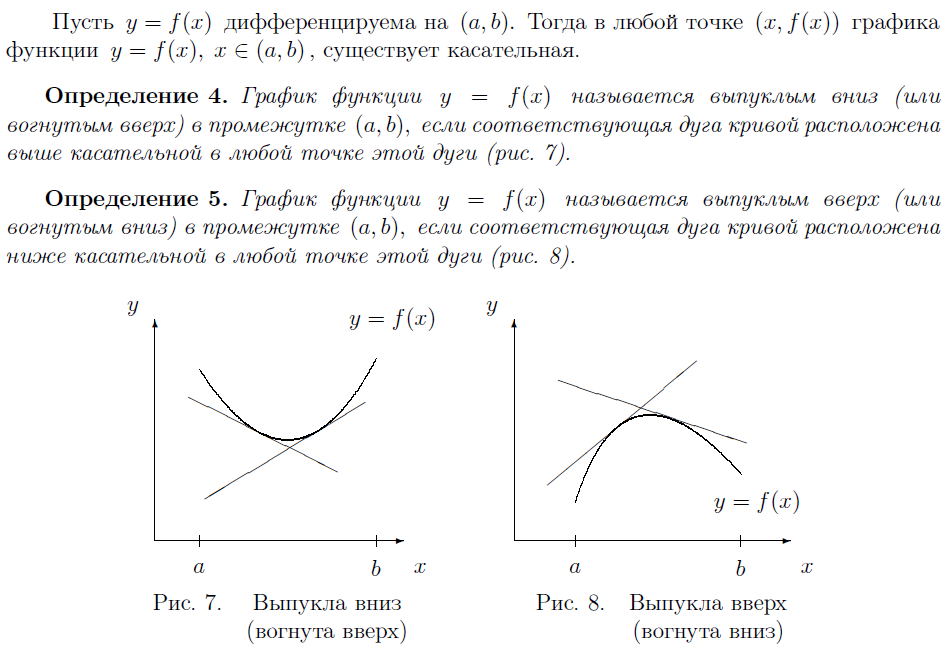
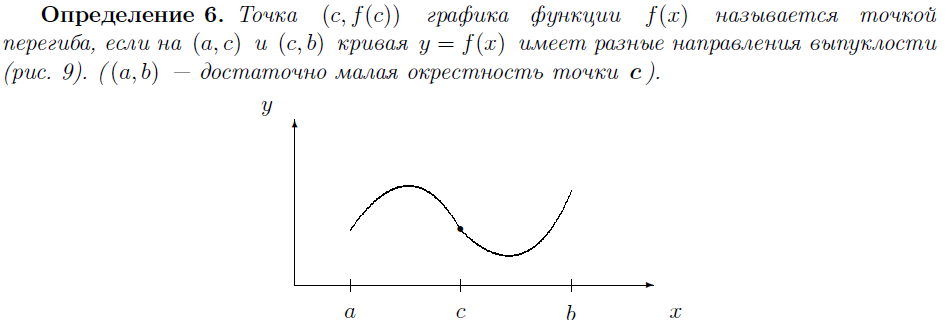
25. ВЫПУКЛЫЕ И ВОГНУТЫЕ ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА. ДОСТАТОЧНЫЕ УСЛОВИЯ ВЫПУКЛОСТИ И ВОГНУТОСТИ ФУНКЦИИ (ПО ВТОРОЙ ПРОИЗВОДНОЙ). НЕОБХОДИМЫЕ, ДОСТАТОЧНЫЕ УСЛОВИЯ ТОЧКИ ПЕРЕГИБА.
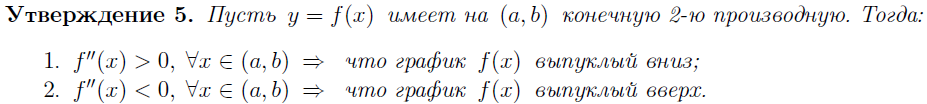
26. АСИМПТОТЫ ФУНКЦИЙ И ИХ НАХОЖДЕНИЕ.
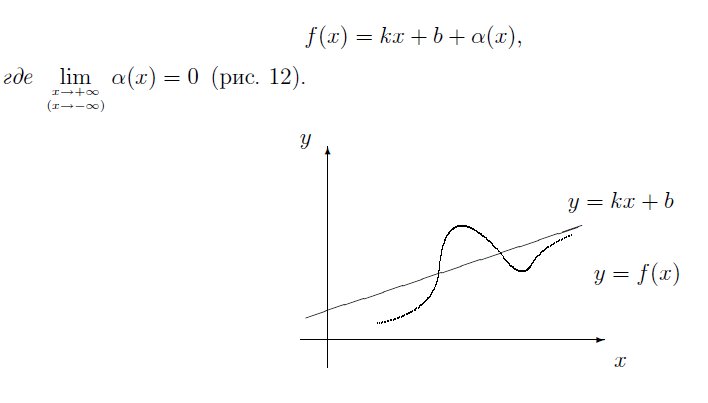
Примеры нахождения см. в лекции 12
27. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА.
28. ФОРМУЛА ТЕЙЛОРА.
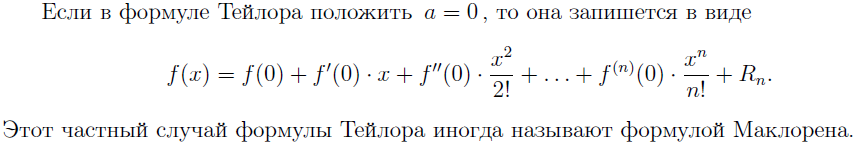
29. ОПРЕДЕЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И МНОЖЕСТВО ЗНАЧЕНИЙ, ГРАФИК ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ. ЛИНИИ И ПОВЕРХНОСТИ УРОВНЯ.
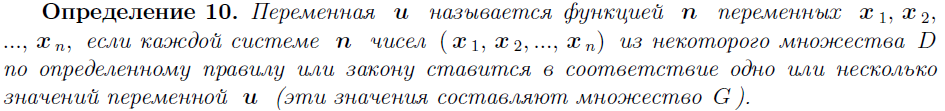
30. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
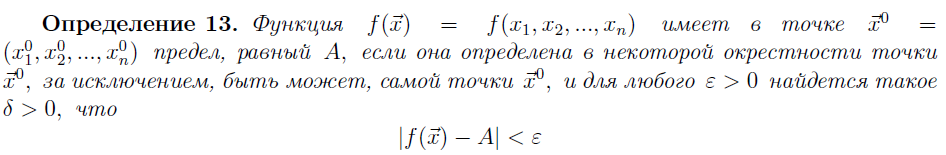
31. ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. РАВЕНСТВО СМЕШАННЫХ ПРОИЗВОДНЫХ.
32. ДИФФЕРЕНЦИРУЕМОСТЬ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ДОСТАТОЧНЫЕ УСЛОВИЯ ДИФФЕРЕНЦИРУЕМОСТИ. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ.
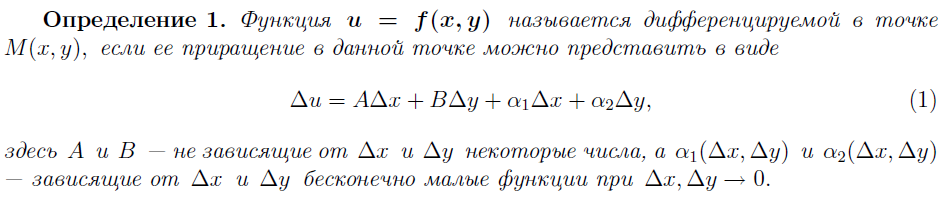
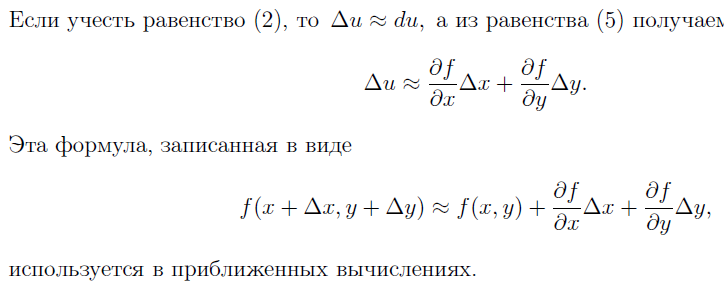
33. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ К ПОВЕРХНОСТИ. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ.
Пусть М – точка поверхности S. Плоскость, содержащая точку М и обладающая тем свойством, что расстояние от этой плоскости до переменной точки M1поверхности S является бесконечно малым по сравнению с расстоянием ММ1, называется касательной плоскостью к поверхности S в точке М. Если поверхность в трехмерном пространстве задана уравнением f(x; y; z) = 0, где функция f достаточное число раз дифференцируема, то уравнение плоскости, касательной к этой поверхности в точке М(хМ; уМ; zМ), имеет вид:
,
(**)
где 
–
частные производные (см. Производная
функции)
функции трех переменных f(x; y; z)
по этим переменным.
Если же поверхность
задана уравнением, разрешенным
относительно аппликаты z,
т.е. имеет вид z = z(x; y),
то уравнение (**) касательной плоскости
принимает вид:
(конечно, предполагается, что функция z имеет непрерывные первые частные производные).
34. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
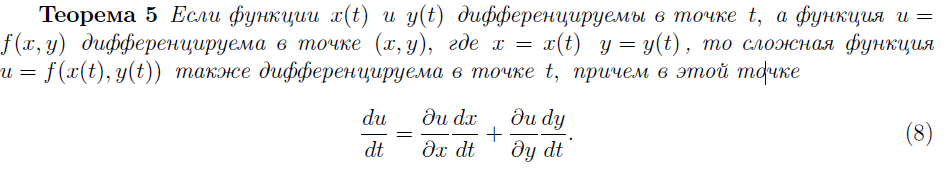
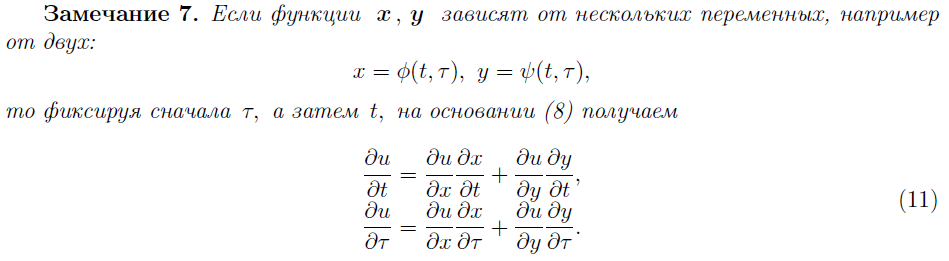
35. ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
36. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ. ГРАДИЕНТ И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.
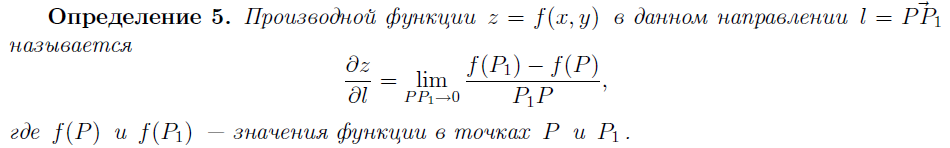
37. ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ИССЛЕДОВАНИЕ НА ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИЙ.
38.
УСЛОВНЫЙ ЭКСТРЕМУМ И ЕГО НАХОЖДЕНИЕ,
МЕТОД ЛАГРАНЖА.
39. ФОРМУЛА ТЕЙЛОРА ДЛЯ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ.
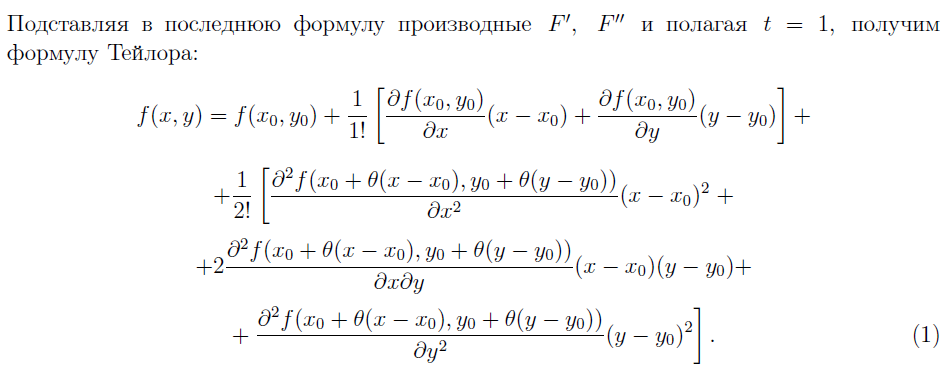
40. Первообразная функция и ее свойства. Примеры. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Определение первообразной и неопределенного интеграла
Функция F(x) называется первообразной функции f(x), если
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
где С - произвольная постоянная.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины.
Таблица интегралов
В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица первообразных
