Міністерство освіти і науки, молоді та спорту України

Національний університет: “Львіська політехніка”

Звіт

до лабораторної роботи

на тему “Потокові алгоритми”

з курсу: “Дискретні моделі в САПР”

Виконав: ст.гр КНз -41

Плакса Віталій

Львів – 2013 р.

1. Мета роботи

Метою даної лабораторної роботи є вивчення потокових алгоритмів.

2. Короткі теоретичні відомості вступ.

Останнім часом значно зросла зацікавленість учених та практиків потоковими

моделями. Це пов’язано із впровадженням та активним розвитком різноманітних територіально розподілених систем: трубопровідних, транспортних, телекомунікаційних та ін. Основою таких систем є певна мережа (мережа трубопроводів, доріг, каналів зв’язку тощо), в якій циркулюють певні потоки (потоки речовин, транспорту, даних тощо), тому задачі, які доводиться розв’язувати при проектуванні та експлуатації систем з мережною структурою, часто зводяться до розробки математичних моделей розподілу потоків та постановки і розв’язання відповідних оптимізаційних задач.

Відомі моделі розподілу потоків у мережах базуються на поняттях теорії графів. Це пов’язано з тим, що граф дає можливість наочно відобразити структуру мережі, а параметри його вузлів і дуг – представити основними числовими характеристиками її елементів. Набір характеристик залежить від природи модельованої системи, а також характеру розв’язуваних задач, однак у потокових моделях їх, як правило, представляють такими параметрами, як зовнішній потік у вузлі, потік по дузі, пропускна здатність дуги, вартість передавання одиниці потоку по дузі тощо. Потокові задачі, як правило, зводяться до пошуку такого розподілу потоків у мережі, при якому б забезпечувався екстремум деякого критерію. При цьому мають враховуватися обмеження, що накладаються умовами збереження потоків у вузлах і неперевищення потоками пропускної здатності дуг. Типовими потоковими задачами є задача про потік мінімальної вартості, про максимальний потік, транспортна задача, задача про призначення та інші. Для їх розв’язання розроблено чимало ефективних алгоритмів, сформувався навіть відповідний напрям обчислювальних методів під назвою потокового програмування

Поняття про потоки

Потік-визначає спосіб пересилання деяких об’єктів з одного пункту в інший.

Розв’язання задачі потоку зводиться до таких основних підзадач:

 Максимізація сумарного обсягу перевезень

 Мінімізація вартості пересилань предметів з одного пункту в інший

 Мінімізація часу перевезень в заданій системі

Сітка - це граф, в якому кожній дузі приписана деяка пропускна здатність. Введемо позначення: с(х,у) - пропускна здатність дуги (х,у), а(х,у) - вартість переміщення одиниці потоку по дузі (х,у), T(x,y) - час проходження потоку, k(x,y) - коефіцієнт підсилення потоку в дузі (x,y).

Припустимо, що є граф, в якому деяка кількість одиниць потоку проходить від джерела до стоку і для кожної одиниці потоку відомий маршрут руху. Назвемо кількість одиниць, що проходять по дузі (х,у), потоком в даній дузі. Будемо потік в дузі(х,у)

позначати через f(х,у) вочевидь 0  f(х,у)  с(х,у). Дуги графа можна віднести до трьох

різних категорій:

1) дуги, в яких потік не може ні збільшуватись, ні зменшуватись (множина таких дуг позначається через - N);

2) дуги, в яких потік може збільшуватись (множина таких дуг позначається через - І);

3) дуги, в яких потік може зменшуватись (множина таких дуг позначається через - R);

Наприклад, дуги, що мають нульову пропускну здатність або значну вартість проходження потоку, повинні належати множині N. Дуги, в яких потік менше пропускної здатності, повинні належати множині I. Дуги, по яких вже проходить деякий потік, повинні належати множині R. Дуги з множини I називають збільшуючими, а дуги з множини R - зменшуючими.

Будь-яка дуга графа належить хоча б одній з трьох введених множин - I, R або N. Можливо, що якась дуга належить як множині I, так і множині R. Це має місце в тому випадку, коли по дузі вже протікає деякий потік, який можна збільшувати чи зменшувати. Відповідні дуги називаються проміжними.

Позначимо через і(х,у) максимальну величину, на яку може бути збільшений потік в дузі (х,у). Відповідно позначимо через r(х,у) максимальну величину, на яку може бути зменшений потік в дузі (х,у). Очевидно,

і(х,у) = с(х,у) - f(х,у) , а r(х,у) = f(х,у)

Припустимо, що ми хочемо переслати додаткову кількість одиниць потоку з витоку в стік. Можливі декілька способів розв’язування даної задачі (якщо вона взагалі має рішення):

1) Цей спосіб міг би бути реалізований, якщо б ми знайшли шлях Р з вершини “s” у вершину “t”, який би цілком складався із збільшуючих дуг (рис.1). Скільки в цьому випадку можна було б додатково переслати одиниць потоку з “s” в “t” по шляху Р?

Оскільки і(х,у) являє собою максимально можливе збільшення потоку в дузі (х,у), то величина додаткового потоку з “s” в “t” по шляху Р буде складати:

min {i(х,у)} (х,у) є Р

s a b t i(s,a)=3 i(a,b)=2 i(b,t)=1

Рис.1. Ланцюг, що збільшує потік і включає лише прямі дуги.

Для даних прикладу ( рис.1) по шляху Р можна переслати з “s” в “t” максимум одну додаткову одиницю потоку, оскільки:

min{i(s,a), i(a,b), i(b,t)} = min{3, 2, 1}=1

2) Цей спосіб міг би бути реалізований, якщо б ми знайшли шлях Р з вершини “t” в вершину “s”, який цілком складався би із зменшуючих дуг (рис.2). При цьому можна було б зменшити потік в кожній дузі (х,у), що привело б до зменшення потоку з вершини “t” в вершину ”s”, тобто, до збільшення чистого потоку з вершини “s” в вершину “t”. На яку максимальну величину можна було б зменшити потік з витоку в стік по вказаному шляху? Оскільки в кожній дузі (х,у) шляху Р потік можна зменшити на максимальну величину r(х,у), то максимальне зменшення потоку вздовж шляху Р визначається величиною

min {r(х,у)} (х,у) є Р

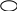
s a b t r(a,s)=1 r(b,a)=2 r(t,b)=1

Рис.2. Ланцюг, що збільшує потік і включає лише зворотні дуги.

Для даних прикладу на рис.2 по шляху Р можна переслати назад з “t” в “s” максимум одну одиницю потоку, оскільки:

min{r(t,b), r(b,a), r(a,s)} = min{1, 2, 1}=1

3)Цей спосіб є комбінацією двох попередніх. Це означає, що необхідно знайти ланцюг, що з’єднує вершини “s” і “t”, дуги якого задовольняють наступним умовам:

- всі прямі дуги ланцюга, що мають напрям від “s” до “t”, належать множині I; - всі зворотні дуги ланцюга, що мають напрям від “t” до “s”, належать множині R.

Для прикладу розглянемо ланцюг С, що з’єднує вершини “s”,”t” і зображений на рис.3. Прямі дуги цього ланцюга (s,a), (a,b), (d,t), а зворотні - (c,b) i (d,c). Якщо кожна пряма дуга належить множині I, а кожна зворотна дуга - множині R, то вздовж розглянутого ланцюга можна переслати додатковий потік з “s” в “t”.

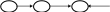
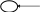s a b c d t i(s,a)=4 i(a,b)=3 r(c,b)=5 r(d,c)=2 i(d,t)=3

Рис.3. Ланцюг, що збільшує потік і включає прямі і зворотні дуги.

Це здійснюється шляхом збільшення потоку в прямих дугах, що є збільшуючими, і зменшення потоку в зворотних дугах, що є зменшуючими. Максимальна величина додаткового потоку, який можна переслати вздовж відповідного ланцюга з “s” в “t”, визначається як мінімум з наступних двох величин:

min {i(x,y):(x,y) - пряма дуга}

min {r(x,y):(x,y) - зворотна дуга}

Мінімальна з двох вказаних величин називається максимальним збільшенням потоку по відповідному ланцюгу. Для прикладу на рис.3, маємо можливе збільшення потоку в прямих дугах i(s,a)=4, i(a,b)=3, i(d,t)=3. Мінімум з цих трьох величин рівний 3. Можливе зменшення потоку в зворотних дугах визначають величини r(c,d)=5, r(d,c)=2. Мінімум з цих двох величин рівний 2. Максимальне збільшення потоку по ланцюгу С дорівнює min(3,2)=2. Таким чином, в результаті збільшення на дві одиниці потоку в прямих дугах і зменшення на дві одиниці потоку в зворотних дугах по ланцюгу можна додатково переслати з “s” в “t” дві одиниці потоку.

Кожен ланцюг з “s” в “t” будь-якого з трьох розглянутих вище типів, по якому можуть бути додатково переслані одиниці потоку, називається збільшуючим ланцюгом.