Системные исследования в бурении

Термин «система» в настоящее время широко используется в различных облас­тях техники и технологии. Что же мы понимаем под системой?

Л. Барталанфи дает следующее определение: «Система - совокупность взаимо­связанных элементов, которые обычно дополняются множеством самых различных характеристик».

Любая система характеризуется:

- составом;

- структурой;

- функцией элементов.

Полное понимание объекта предполагает умение видеть его не только как цель­ность, но понимать, на чем эта цельность держится. При таком понимании исследо­ватель выделяет слабые и сильные стороны объекта, связи его со смежными объек­тами, замечает пробелы в этих связях.

Если в системе происходят необратимые изменения, когда возникают новые си­туации, то такие системы называются развивающимися.

Связи между элементами могут быть функциональными, корреляционными и т.п. Сложные системы могут быть расчленены на подсистемы, и их решение осуще­ствляется по частям (подсистемам). Отдельные подсистемы составляют различные иерархические уровни, каждый из которых характеризуется не только присущими им свойствами, но и своими целями. Такой единообразный методологический подход к изучению самых различных объектов в известной степени позволил формализовать их изучение и называть сис­темами.

В первую очередь, следует учитывать те элементы, которые определяют основ­ные (ключевые) состояния системы.

Однако, желание максимально упростить систему, в ряде случаев, может при­вести к излишнему упрощению модели. На первом этапе обычно создается упрощенная (концептуальная) модель, которая в дальнейшем проверяется и уточняется. Следующим шагом является стадия расщепления или симатической раздробленности, когда об объекте судят с разных позиций, например с позиции производительности или стоимости, или стабильности и т.д.

Система подвергается как внутреннему микроанализу (структура, свойства), так и макроанализу (взаимодействие с внешней средой).

Важным свойством системы является ее эмерджентность - когда показатели, ха­рактеризующие ее в целом, не являются суммой свойств отдельных ее элементов.

Наиболее просты так называемые дискретные системы, в которых элементы из­меняются дискретно и принимают "п" независимых состояний.

Большинство переменных, с которыми приходится иметь дело в процессе буре­ния, относится к классу случайных величин. Если элементы системы не зависят друг от друга, или слабо связаны, то это и определяет неопределенность системы.

В сложных системах приходится руководствоваться не столько строгими зако­номерностями, сколько симптомами и тенденциями. Естественно, что величина не­определенности в таких системах весьма велика. Сложные системы в целом ряде случаев подразделяются на подсистемы, что облегчает их изучение.

Процесс бурения - система с множеством элементов, находящихся в связях и отношениях друг с другом и образующих определенное единство. Элементы систе­мы изменяются во времени и пространстве, функционально и корреляционно связа­ны между собой. Такие системы часто называются диффузными [10, 32].

ФОРМУЛИРОВКА ПРОБЛЕМЫ

Проблема - такая ситуация, когда существующее состояние объекта (процесса) не соответствует представлениям о нормальном его состоянии, т.е. достигнутый уровень функционирования объекта ниже желаемого.

Проблема характеризуется:

■ целью и задачами;

■ затратами ресурсов на каждый курс действий;

■ критериями оптимизации;

■ параметрами и структурой объекта;

■ моделью (моделями), в которых с помощью формального языка отражают­ся связи между целями, альтернативными затратами и т.д.

Формулировка проблемы не делается сразу. Вначале изучается объект, устанав­ливаются некоторые симптомы его поведения, потом тенденции. И лишь только по­сле этого формулируется проблема. Формулировка проблемы — операция эвристи­ческая.

Каждая проблема оценивается с позиций:

■ полноты решения;

■ ресурсов, которые потребуются для ее решения;

■ имеющихся в наличии ресурсов;

■ экономического, технологического и других эффектов.

СИСТЕМНЫЙ ПОДХОД И СИСТЕМНЫЙ АНАЛИЗ

Сущность системного подхода заключается в том, что он соединяет в себе зада­чи анализа и синтеза.

Одной из ключевых проблем является разработка и использование представле­ний о целостности системы.

Системный подход включает в себя:

■ определение сущности и цели объекта;

■ установление места и времени объекта;

■ формализацию объекта и задач исследования;

■ определение проблемы.

Системный анализ включает в себя операции принятия решений, часто в услови­ях неопределенности.

Системный анализ - метод системных исследований, синтезирующий методы исследования операций и системотехники.

Центральной процедурой системного анализа является построение обобщенной модели, которая отражает все факторы, задействованные при анализе системы. В модели должны быть отражены следующие позиции:

■объект рассматривается как множество, состоящее из элементов и их свойств, составляющих единое целое;

■ должны быть определены цели исследования;

■ необходима формулировка конкретных задач;

■ должен быть обозначен язык описания системы.

Описание системы производится не как сумма описаний ее частей, а как целост­ное описание системы, в том числе ее связи, качества и т. д.

Системный подход широко используется при построении различных классифи­каций. Любая классификация базируется на принятой проблеме или главной цели (целях). Иерархическая структура системы выражается в виде "дерева целей" [32].

Уровень 1 называют корневой вершиной, или стволом, уровень 2 - ветвями пер­вого яруса (уровня), уровень 3 - ветвями второго яруса, а уровень 4 - листьями.

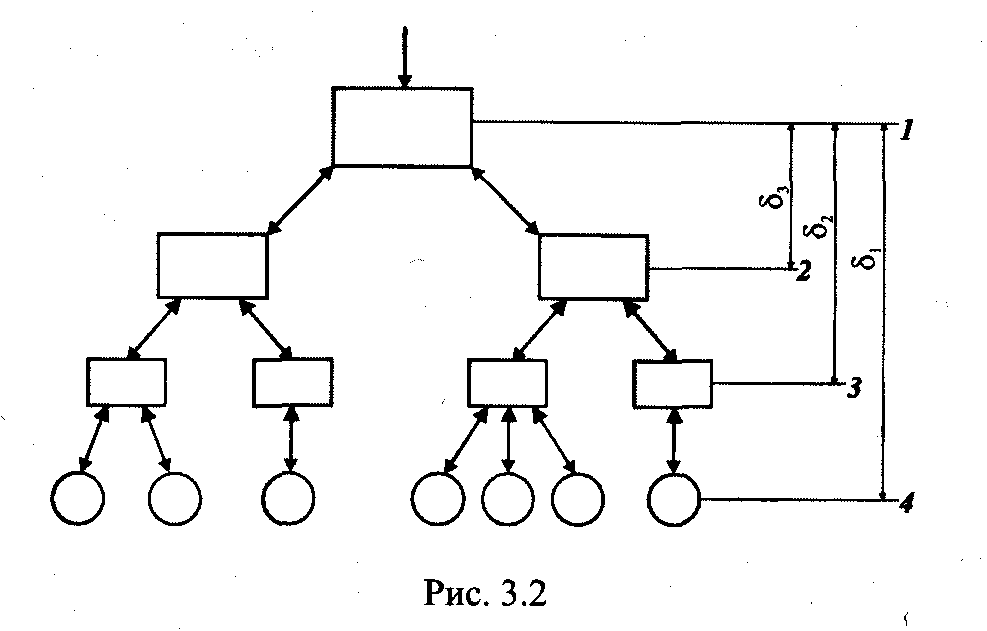
На каждом уровне, кроме верхнего, вводятся критерии оценки. Например, α -оценка экономической эффективности, β - сроков выполнения работ, j - выполнения целевого задания. Следующий уровень предусматривает формулировку способов достижения целей, устанавливается вес каждого критерия: q_a, q_β, q_j, а также опреде­ляются коэффициенты значимости по каждому критерию и цели S:

где п - число целей.

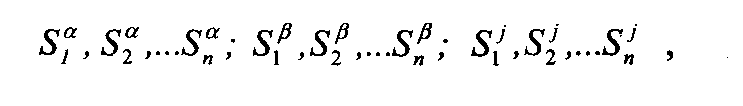
При этом выполняются следующие нормирующие условия

:

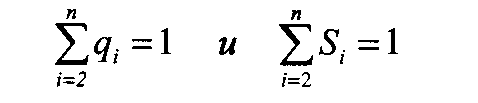Вклад каждой цели в выполнение программы на данном уровне иерархии оценивается коэффициентом связи

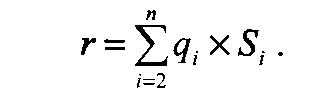
Результаты расчетов сводятся в матрицу сопоставления целей. Вклад каждой це­ли в выполнение программы оценивается коэффициентом относительной важности

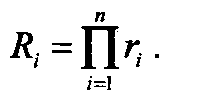
Чем больше R_i тем весомее цель i-ой программы, тем она больше требует ресур­сов.

Пример.

В качестве примера рассмотрим идеи системного подхода к исследованию процесса бурения алмазным инструментом. Традиционно этот процесс обычно рассматривается как разрушение горной породы рабочим органом (долото, коронка). Такие же процессы, как эвакуация продуктов разрушения и охлаждение инструмента, рассматриваются чаще всего как самостоятельные. Попытки совместного рассмотрения этих процессов в рамках традиционных методов оказываются чрезвычайно громозд­кими и мало эффективными.

Примем следующие допущения:

■ все алмазы в ряду "резания" внедрялись на одинаковую глубину;

■ ось вращения буровой коронки не смещается;

■ коронка вращается с постоянной частотой вращения.

Под действием осевого усилия алмаз внедряется в породу на глубину h_p, между матрицей и забоем существует зазор h₃, по которому циркулирует промывочный раствор, производится удаление продуктов разрушения и охлаждение алмазов.

Сущность системного подхода предусматривает рассмотрение процесса разрушения породы не единичным алмазом, а группой алмазов (сектором), в увязке с эвакуацией продуктов разрушения и охлаждением алмазов.

Увеличение параметра h_p за счет уменьшения h₃ приводит к ухудшению условий эвакуации шлама и охлаждению алмаза. Уменьшение значений параметра h_p снижает скорость бурения и может привести к заполированию алмазов. Поэтому для пары "коронка-порода" существует оптимальное соотношение:

где к_п - коэффициент, учитывающий скол породы.

Показатель ε интегрально характеризует не только процесс разрушения горной породы алмазом, но также эвакуацию разрушенной породы и охлаждение алмаза, что позволяет его определить в качестве доминантного признака функционирования системы бурения.

ПРОЦЕСС БУРЕНИЯ - КИБЕРНЕТИЧЕСКАЯ СИСТЕМА

Кибернетические системы характеризуются способностью элементов восприни­мать, хранить, перерабатывать информацию и использовать ее для управления в ус­ловиях взаимодействия с окружающей средой в соответствии с выработанными це­лями. Такие системы получили название "черного ящика" [10, 32]. Процесс бурения можно рассматривать как систему "черного ящика" (рис. 3.3).

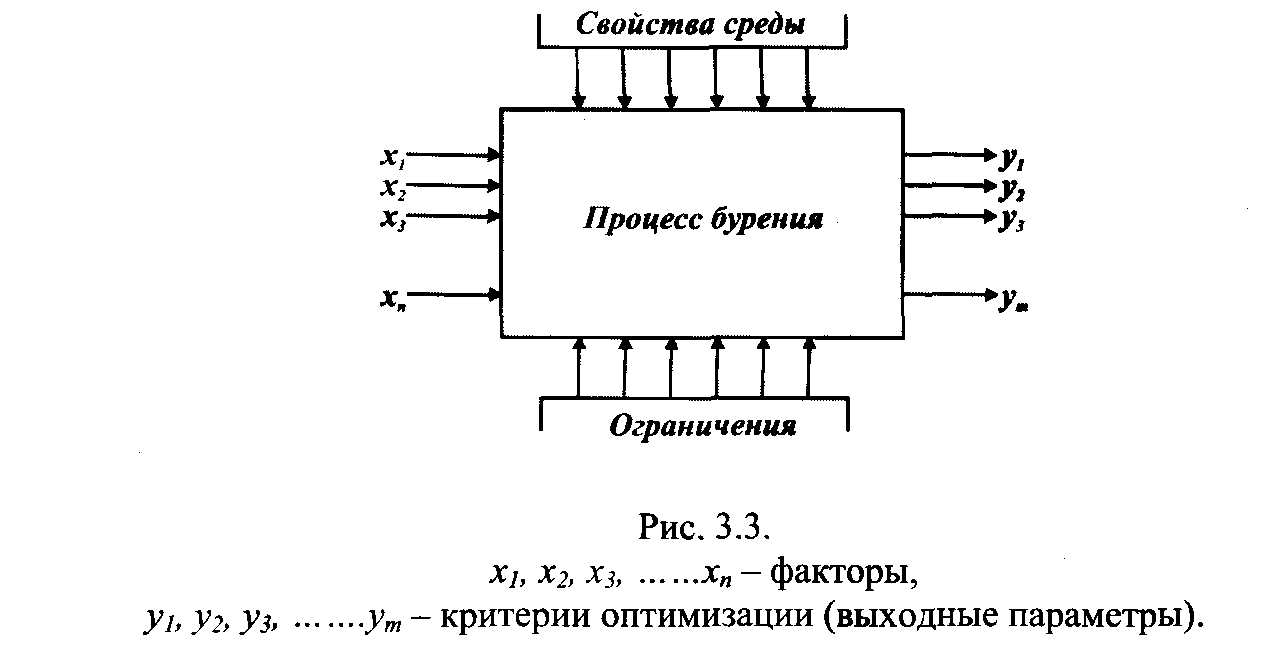
Выходные сигналы кибернетической системы характеризуют состояние системы и являются целями оптимизации, называемыми критериями оптимизации.

Критерии оптимизации определяют основные характеристики процесса бурения:

• стоимость;

• производительность;

• качество работ;

• безопасность работ.

МЕТОД ГРАФОВ-СВЯЗЕЙ

При решении многих технологических, конструкторских и других задач удобнее иметь дело с моделями, которые легко образуются, если отдельные элементы объекта (конструкция, процесс и т. д.) принять за точки, а связи между ними - за линии.

Например, если элемент А воздействует на элемент В, то это обозначается: a>В.

Схема А → В → С обозначает посредственное воздействие элемента А на эле­мент С через В.

Связь 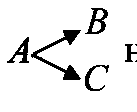называется связью сопутствия элемента А с В и С.

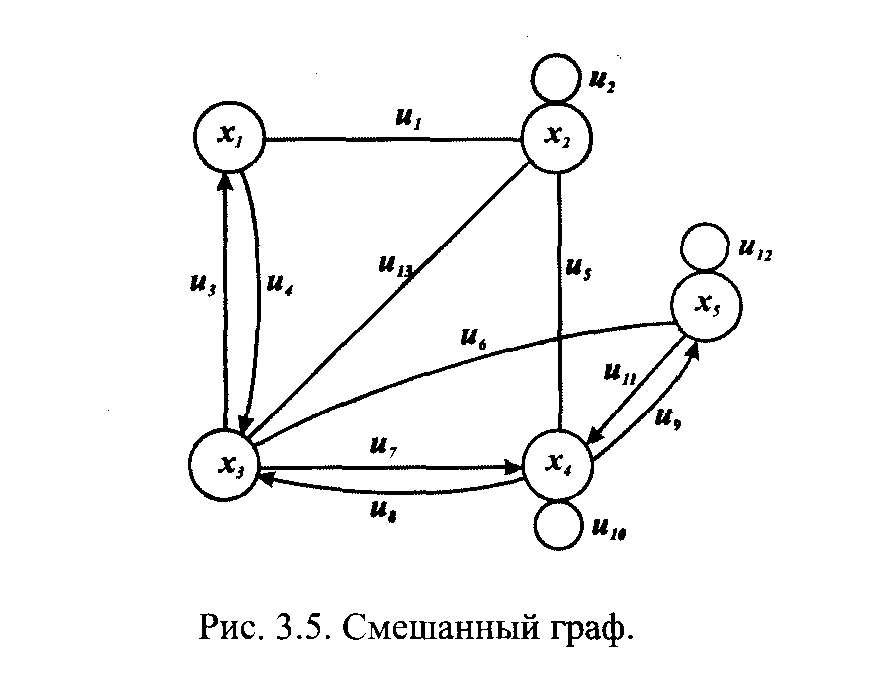
Объект, состоящий из двух множеств (множества точек и множества линий), ко­торые находятся между собой в некотором отношении, называют графом.

Метод позволяет установить причинно-следственные связи между элементами системы, и что не менее важно, дать прогноз ее функционирования. Известно, что связь между элементами может быть представлена в виде матрицы. Причем наличие связи отмечается через 1, а ее отсутствие через 0.

Множество точек графа обозначают: называют множеством вершин. Множество линий, соединяющих пары вершин , называют множеством ребер или дуг и обозначают Графом является объект, который обозначается в виде G = (X, U) и состоит из множества вершин X и множества дуг U, находящихся в некотором соотношении.

ПРОГРАММНО-ЦЕЛЕВОЕ ПЛАНИРОВАНИЕ (ПЦП)

Изучение сложных, слабо структурных и бесструктурных систем представляет большие трудности, поэтому исследователи сталкиваются с необходимостью выбо­ра главных (ключевых) и отбраковки второстепенных проблем. Причем сложные системы могут быть представлены несколькими взаимосвязанными моделями.

ПЦП осуществляется с использованием метода экспертных оценок, заключаю­щегося в выявлении некоторого согласованного мнения группы специалистов-экспертов.

Процесс экспертизы заключается в том, что эксперту предъявляется гипотеза, правомерность которой необходимо выяснить. Эксперт оценивает важность про­блемы и выдает свою персональную вероятностную оценку. В качестве гипотезы могут выступать цели системы, которые ранжируются по степени важности. Для большей объективности прямые контакты между экспертами исключаются. В каче­стве экспертов привлекаются высококвалифицированные специалисты. Эксперт должен иметь возможность получить интересующую его информацию.

Составной частью ПЦП является метод экспертных оценок. Эксперты дают свою оценку каждому направлению исследований (табл. 3.6).

Таблица 3.6

Экспертная анкета

Эксперт	Шифр направления
	1	2	……..	j	……..	п
1	С11	С12		С1j		C1n
2	С21,	С22		C2J		С2n
i	Сi1	Ci2		Cij		Сin
т	Cm1	Ст2		Cmj		Cmn

Каждый i-ый эксперт дает оценку с учетом коэффициента относительной важно­сти для каждой у_i-й проблемы. Отметим, что темы могут оцениваться и по другим качествам, например, по взаимной полезности или состоянию - срок.

Результаты анкет сводятся в таблицу.

Результаты обрабатываются математическими методами.

Мнения экспертов представляются в виде экспертных оценок, в баллах или ран­гах. Максимальная оценка обычно не превышает 10 баллов [10, 46]. Если оценки ранжируются, то единица присваивается максимальной оценке, а число 0 - мини­мальной. В случае, когда среди оценок i-го эксперта есть одинаковые, то им при­сваиваются порядковые числа натурального ряда, а затем всем одинаковым оценкам назначается одинаковый ранг, равный среднему арифметическому соответствую­щих порядковых чисел натурального ряда.

Сумма рангов S_j, для j-го направления представляет собой сумму, взятую для рангов R_ij из таблицы 3.6.

Показатель связанных (равных) рангов-оценок T_i назначенных i-ым экспертом, определяется по формуле:

(3.39)

где L - число групп связанных рангов, L=1÷l - число связанных рангов в i-ой группе.

Согласованность мнений экспертов оценивается по коэффициенту конкордации -W_k/:

Если имеется полная согласованность экспертов, то W=l. При полной несогла­сованности экспертов W=0 ста­вить под сомнение согласованность мнений экспертов .

АНАЛИТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЙ

Становление и развитие техники и технологии бурения скважин, как научной дисциплины, было связано, в первую очередь, с развитием аналитических методов исследований. Большой вклад в их развитие внесли Н. С. Успенский, В. С. Федоров, Р. И. Шищьнко, Б. И. Воздвиженский, Е. Ф. Эпштейн, А. X. Мирзаджан-заде, М. А. Александров, Н. И Шацов, П. В. Балицкий, В. С. Владиславлев, Р. М. Эйгелес, Г. М. Саркисов, А. О. Сароян, Б. Б. Кудряшов, Б. М. Ребрик, Л. К. Горшков, Б. Н. Кутузов, В. Г. Кардыш, В. В Калыгин, Б. А. Катанов и др.

Еще 15-20 лет тому назад многими специалистами разделялось мнение, что привлечение знающих математиков-аналитиков к решению разнообразных задач техники и технологии бурения, позволит найти в этих направлениях революцион­ные решения. Однако, время, прошедшее с тех пор, убедительно показало, что та­кие предсказания не сбылись. Не сбылись не из-за того, что были привлечены не­компетентные аналитики, а из-за того, что стоящие задачи стали неразрешимыми перед аппаратом этих методов.

Аналитические методы в настоящее время с успехом и широко используются для решения классических, экстремальных задач, приведения целевых функций к линейному виду, формулированию и решению задач нелинейного программирова­ния и др.

Аналитические методы в литературе часто называют также детерминированны­ми или теоретическими [14].

Преимуществами аналитических методов являются их небольшая стоимость и трудоемкость, возможность представить результаты в виде расчетных формул, гра­фиков и т. д. Эти методы требуют априорной информации об объекте, либо эта ин­формация может быть получена в результате эксперимента.

Аналитические методы основаны на использовании фундаментальных законов физики, химии, математики и т. д. В качестве аппарата исследований применяются методы теоретической механики, гидравлики, вероятностные методы и др.

На первом этапе выбирается концептуальная модель, устанавливаются внешнее и внутреннее подобие. Под внешним правдоподобием понимается выбор модели и оценка ее адекватности. Под внутренним правдоподобием понимается ожидаемая степень точности решения полученных уравнений, принятых в концептуальной мо­дели.

В случае, когда вид модели уже выбран, то внешнее правдоподобие модели счи­тается осуществленным и выбор метода исследования определяется условиями внутреннего правдоподобия [46].

Эффективность выбора концептуальной модели тем выше, чем больше имеется сведений об объекте. Такие сведения могут быть получены из. результатов предва­рительных исследований, произведенных в сходных условиях.

ПРИНЯТИЕ ОПТИМАЛЬНЫХ РЕШЕНИЙ С ПОМОЩЬЮ МЕТОДА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Задачи линейного программирования обычно сводятся к необходимости макси­мизировать или минимизировать некоторую количественную величину с учетом ря­да ограничений. Целевая функция и ограничения записываются линейными уравне­ниями. Задача линейного программирования имеет вид:

W = ф(а, х) → max(min) ,

где а - заданные условия;

х - элементы решений, x=(x₁,x₂, ... х_n); п - число решений (n-мерный вектор).

Линейное программирование используется для оптимизации процессов, связан­ных с распределением ресурсов, организацией работ, решением транспортных задач и др.

Трудности решения задачи определяются количеством элементов решения, ви­дом функциональной зависимости, связывающей показатель эффективности с эле­ментами решения, и от ограничений, налагаемых на элементы решения.

Условия применения метода линейного программирования.

• показатель эффективности W линейно зависит от элементов решения x₁, х₂, ... х„;

• ограничения, налагаемые на элементы решения, представлены линейны­ми равенствами или неравенствами относительно х₁, х₂, ... х_n

Любую задачу линейного программирования рекомендуется привести к стан­дартной форме (основная задача линейного программирования ОЗЛП), суть которой заключается в том, чтобы найти неотрицательные значения переменных х₁, x₂, ... х_n которые бы удовлетворяли условиям-неравенствам:

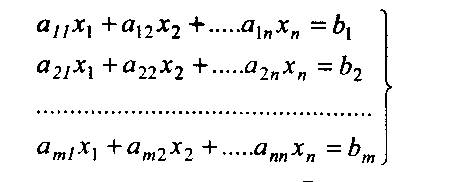
Линейная функция этих переменных должна обеспечивать экстремальные зна­чения:

L = С₁x₁, + С₂х₂ +......С_nx_n→ тax

Трудности решения задач линейного программирования часто возникают в слу­чае некорректной их постановки и задания нереальных ограничений.

Задачи линейного программирования далеко не всегда имеют решения. Назовем наиболее типичные случаи:

• условия равенства общей задачи линейного программирования могут про­тиворечить друг другу в области неотрицательных решений;

• допустимые решения существуют, но целевая функция не имеет оптимума (не ограничена).

Задачи линейного программирования наглядно иллюстрируются графически. Ес­ли число уравнений т, число переменных п=т+2, то интерпретация поставленной задачи может быть представлена на плоскости. Имея в виду n-m=k=2, линейные не­зависимые уравнения-равенства можно разрешить относительно каких-либо т ба­зисных переменных.

В линейном программировании часто приходится сталкиваться с взаимно двой­ственными задачами, когда:

• одна из задач является задачей максимизации, а другая - минимизации, в системе ограничений неравенства;

• записываются со знаком > или <;

• каждому ограничению одной задачи соответствует переменная другой за­дачи; номер переменной совпадает с номером ограничения, при этом ог­раничению, записанному в виде неравенств, соответствует переменная, связанная условиями неотрицательности;

• коэффициенты целевой функции одной задачи соответственно равны сво­бодным членам другой задачи;

• матрица условия одной задачи получается из матрицы условий другой за­дачи с помощью транспонирования.

При решении задач линейного программирования уравнения удобно представлять в виде уравнений “в отрезках”. Например, для уравнения 2x₁+x₂=2: Уравнение в отрезках имеет вид ;

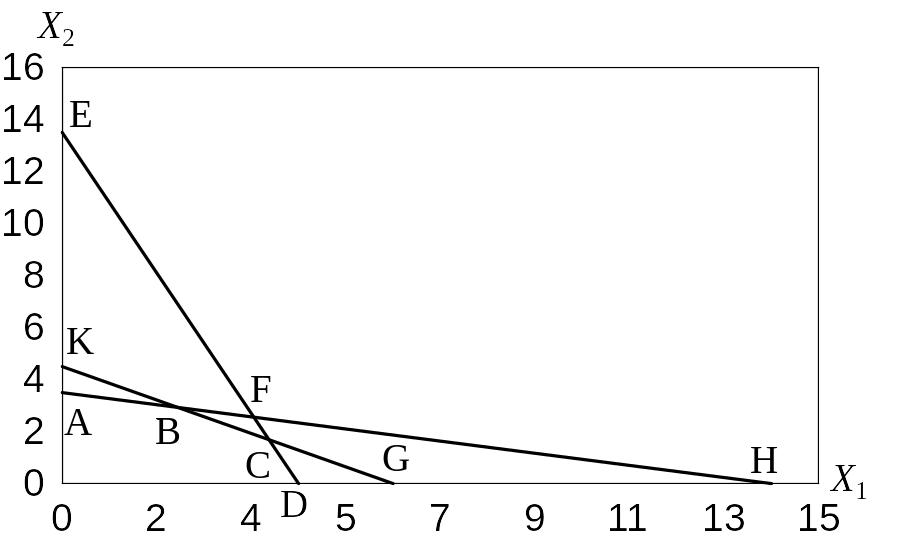
Областью допустимых решений системы линейных неравенств

показана на рисунке и представлена многоугольником ABCD0.

МОДЕЛИРОВАНИЕ ПРОЦЕССА БУРЕНИЯ

Известные методы моделирования условно можно подразделить на следующие две основные группы:

• материальное (предметное);

• абстрактное (абсолютное)

В свою очередь материальное моделирование включает в себя:

• физическое (сохраняется природа объекта);

• предметно-математическое;

• натурное;

• аналоговое.

Абстрактное моделирование состоит из:

• знакового;

• интуитивного (мысленного);

• логико-математического.

Применение различных методов моделирования на первых этапах носит обычно познавательный характер. После интерпретации результатов исследований присту­пают ко второй фазе - переходу к моделированию конкретных условий с целью по­лучения ряда количественных характеристик.

Под моделью понимается мысленно, условно или материально реализованный объект, который отражает основные характеристики реального объекта, замещая его так, что изучение последнего дает новую информацию о нем.

Модель (по латыни - мера, норма, образец) может выступать гносеологическим заместителем оригинала на следующих уровнях:

• на уровне структур;

• на уровне элементов;

• на уровне результатов;

• на уровне функций или поведения.

Модели бывают предметные или материальные и идеальные или абстрактные. Модель строится на основании логических, аналитических и экспериментальных исследований.

Сложные объекты могут быть подразделены на подсистемы (элементы) с уста­новлением их иерархии и связей на различных уровнях иерархии.

Условно все объекты можно подразделить на четыре схемы взаимодействия с внешней средой:

• одномерно-одномерная схема, когда на объект воздействует только один фактор, а выходным параметром является один сигнал;

• одномерно-многомерная схема, отличается от предыдущей тем, что в объ­екте имеется несколько выходных сигналов;

• многомерно-одномерная схема, характеризуется наличием ряда входных и одним выходным сигналом;

• многомерно-многомерная схема, предполагает воздействие на объект ряда сигналов и наличие ряда выходных сигналов.

Одномерно-одномерная схема взаимодействия статически стационарного детер­минированного объекта с внешней средой характеризуется тем, что выходной сиг­нал связан с входным воздействием через постоянный коэффициент:

y=kx и y = y₀+kx

где у - выходной сигнал;

х - входное воздействие (сигнал);

k - постоянный коэффициент;

y_o - начальное значение выходного сигнала.

ОСНОВЫ ТЕОРИИ ПОДОБИЯ

Под подобными явлениями понимаются явления, процессы которых имеют оди­наковую природу, протекают в условиях, характеризующихся постоянством отно­шений одноименных физических параметров.

Геометрическое подобие наблюдается в случаях, когда все размеры пространст­ва, занятого изучаемой системой и моделью, будут изменены в определенное число раз.

Кинематическое подобие имеет место, если сходственные точки изучаемой сис­темы и модели, двигаясь по геометрически подобным траекториям, проходят по­добные пути в промежутки времени, отличающиеся постоянными множителями.

Динамическое подобие наблюдается в случае, когда массы любых сходственных частиц, соответственным образом расположенные в пространстве и во времени, от­личаются друг от друга постоянными множителями.

При моделировании физических процессов целесообразно перейти к безразмер­ным зависимостям между параметрами изучаемых процессов.

У подобных явлений критерии подобия одинаковы.

Физическое моделирование сводится к решению двух самостоятельных задач:

1. Установить параметры модели таким образом, чтобы ее рабочий процесс был подобен натурному.

2. По результатам исследования модели рассчитать параметры или характе­ристики натурного процесса.

Приведем наиболее широко используемые критерии подобия.

24