3.2 Расчет и построение естественных механических и электромеханических характеристик ад

3.2.1 Рассчитываем приведенные сопротивления

- приведенное активное сопротивление ротора,

Ом – приведенное индуктивное сопротивление ротора,

- индуктивное сопротивление КЗ .

3.2.2 Определяем синхронную скорость

,

где f_1н – частота сети, р – число полюсов.

3.2.3 Определяем критический момент двигателя в двигательном режиме

3.2.4 Определяем номинальный момент двигателя

т. к. отношение М_кр/М_н = 2.7, то

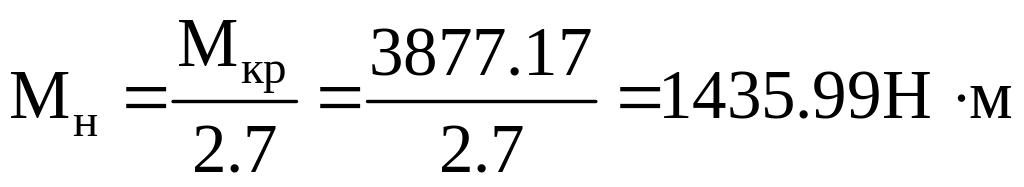
3.2.5 Определяем наибольший пусковой момент двигателя

3.2.6 Определяем момент переключения

3.2.7 Определяем критическое скольжение в двигательном режиме

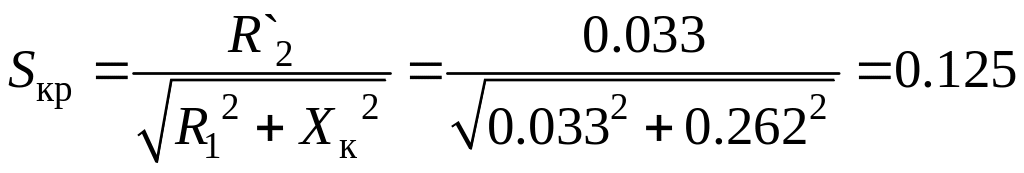
3.2.8 Определяем номинальное скольжение

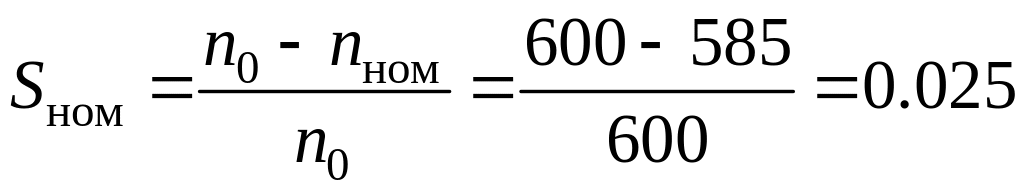
3.2.9 Определяем скольжение по ступеням

ступень 1:

ступень 2:

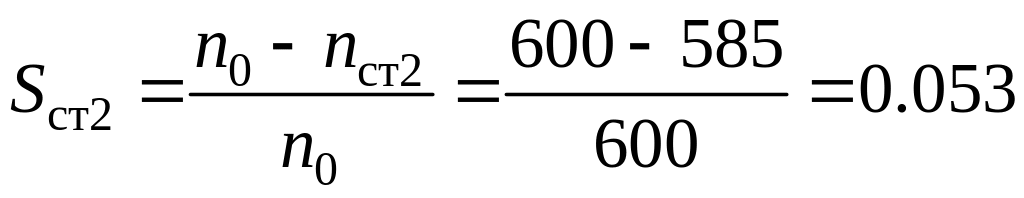
3.2.10 Рассчитываем естественную механическую характеристику М=f(S) по формуле:

,

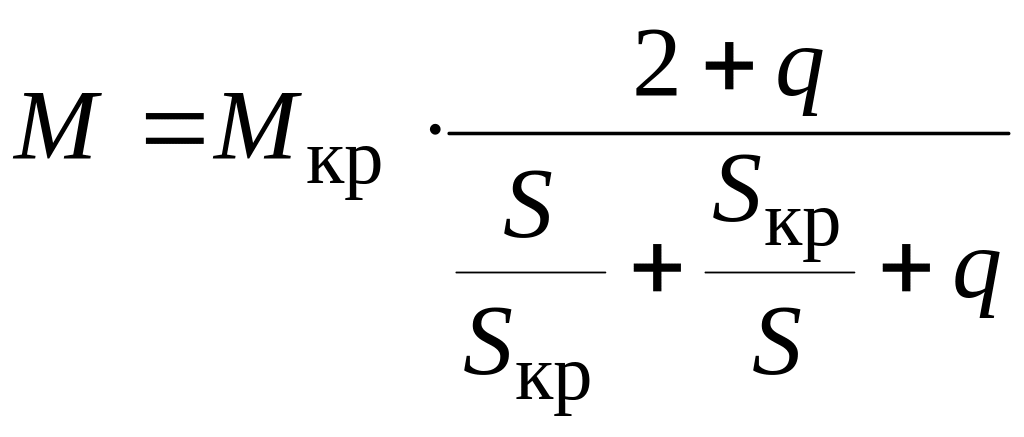где 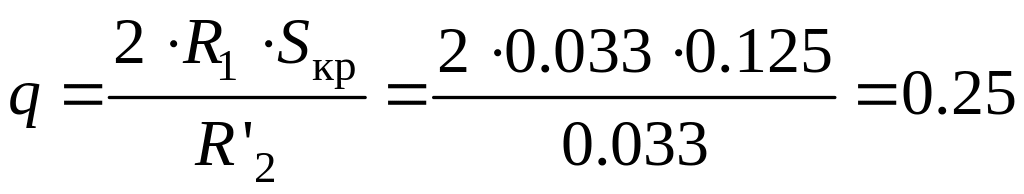- параметр, зависящий от сопротивлений обмоток АД.

Задаемся скольжением от 0 до 1 и строим естественную характеристику М=f(S).

Данные для построения естественной механической характеристики представлены в таблице 1.

Таблица 1 – Данные для построения естественной механической характеристики.

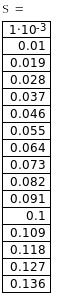
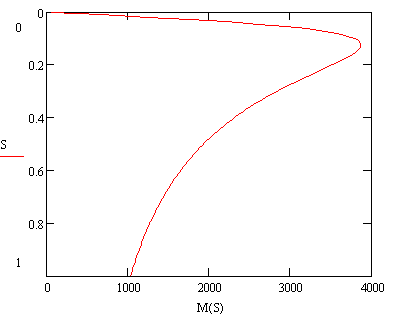
Естественная механическая характеристика представлена на рисунке 6.

3.2.11 Рассчитываем электромеханические характеристики I`₂=f(S), I₁=f(S)

, ,

где α = (0.11 ÷ 0.13).

Принимаю α=0.12

Задаемся скольжением от 0 до 1 и рассчитываем электромеханические характеристики. Данные расчета представлены в таблице 2.

Естественные электромеханические характеристики представлены на рисунках 6,7.

Таблица 2 – Данные для расчета электромеханической характеристики I’₂=f(S),

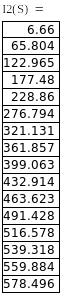
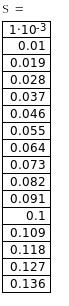
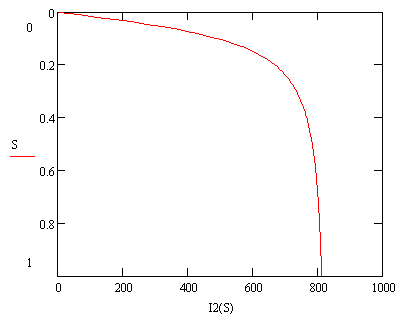
Рисунок 7 – Естественная электромеханическая характеристика I’₂ =f(S)

Таблица 3 – Данные для расчета электромеханической характеристики I₁=f(S),

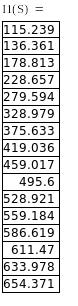
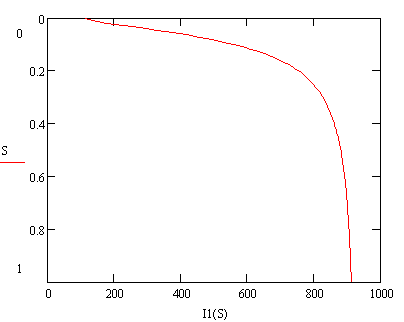
Рисунок 8 – Естественная электромеханическая характеристика I₁ =f(S)

3.3 Пуск и регулирование скорости ад. Расчет механической характеристики.

3.3.1. Расчет эквивалентного генератора:

-э.д.с. эквивалентного генератора

,

-среднее значение напряжения на выходе выпрямительного моста при разомкнутой цепи ростоянного тока и скольжении s=1:

,

где m-число фаз выпрямителя; при m=6 имеем = ,где -э.д.с. на кольцах неподвижного ротора.

B,

,

где- -активное сопротивление эквивалентного генератора,

-сопротивление, учитывающее снижение выпрямленного напряжения вследствие перекрытия вентилей; и -соответственно приведенные к цепи ротора индуктивное и активное сопротивления фазы асинхронного двигателя при скольжении s=1;

при соединении обмоток статора и ротора асинхронного двигателя в звезду

Ом,

Ом;

где - коэффициент трансформации:

;

и - соответственно индуктивное и активное сопротивления фазы обмотки статора;

и - соответственно приведенные индуктивное и активное сопротивления фазы обмотки ротора;

-линейное напряжение на зажимах статора двигателя.

Ом

-индуктивность генератора, эквивалентного асинхронному двигателю:

Гн,

-частота питающего напряжения; и -соответственно индуктивность и сопротивление сглаживающего дросселя;

Гн,

Реактор СД в цепи выпрямленного тока ротора выбирается по номинальному току и требуемой индуктивности L_др.

Гн

где - индуктивное сопротивление фазы ротора;

где =0,122Ом- индуктивное сопротивление статора;

-индуктивное сопротивление фазы ротора, приведенное к статору;

- коэффициент приведения;

- коэффициент трансформации ЭДС.

По значению расчетной индуктивности выбираем токоограничивающий реактор РТСТ-20.5-1.53УЗ.

- индуктивность сглаживающего реактора;

- номинальный фазный ток;

- активное сопротивление обмотки;

- номинальное линейное напряжение;

- масса.

,

где -суммарная индуктивность цепи;

;

где -суммарное сопротивление на первом интервале времени;

;

где - суммарное сопротивление на втором интервале времени;

3.3.2. Определяем добавочные сопротивления для первой ступени характеристики:

,

после приведения к общему знаменателю и некоторых преобразований, получаем:

В результате решения квадратного уравнения получаем два корня

,

.

Принимаем - наибольшее значение из двух корней.

Определяем добавочное сопротивление для пусковой характеристики

, получаем

,

,

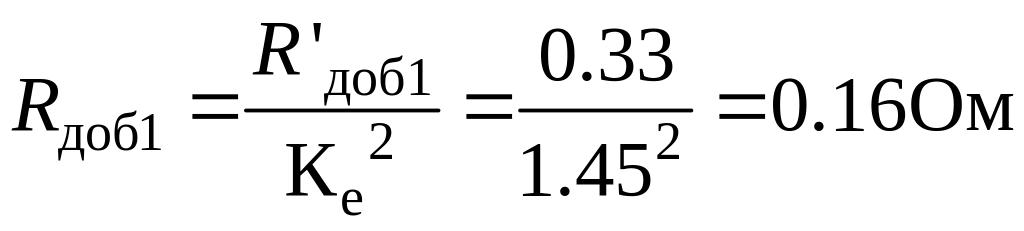где - приведенное добавочное сопротивление,

- добавочное сопротивление для характеристики первой ступени.

Механические характеристики имеют вид, изображенный на рисунке 8:

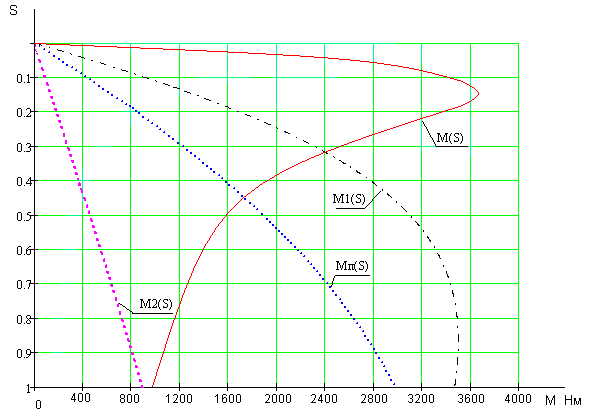
Рисунок 9. Механические характеристики АД в пределах рабочего цикла

3.3.3. Расчет электромагнитных постоянных времени на интервалах периодов коммутации.

;

-электромагнитная постоянная времени в первом интервале периода коммутации;

;

-электромагнитная постоянная времени в втором интервале периода коммутации;

;

;

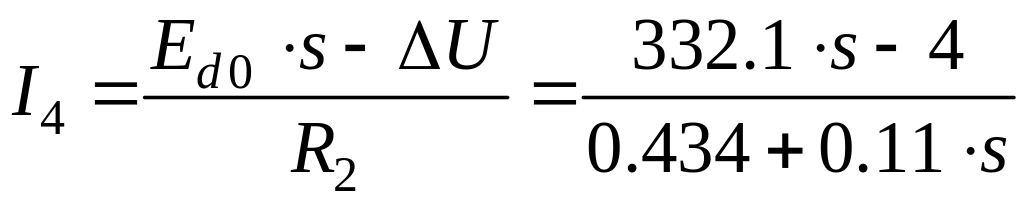где и -соответственно максимальное ( ) и минимальное ( ) значения тока в цепи;

=4В- суммарное падение напряжение в вентилях роторной и трансформаторной групп ( при мостовой схеме соединения вентилей трансформаторной группы следует учитывать падение напряжения в 4 вентилях, причем для кремниевых принимается 1В).

3.3.4. Определение величины среднего значения выпрямленного тока.

;

где ,

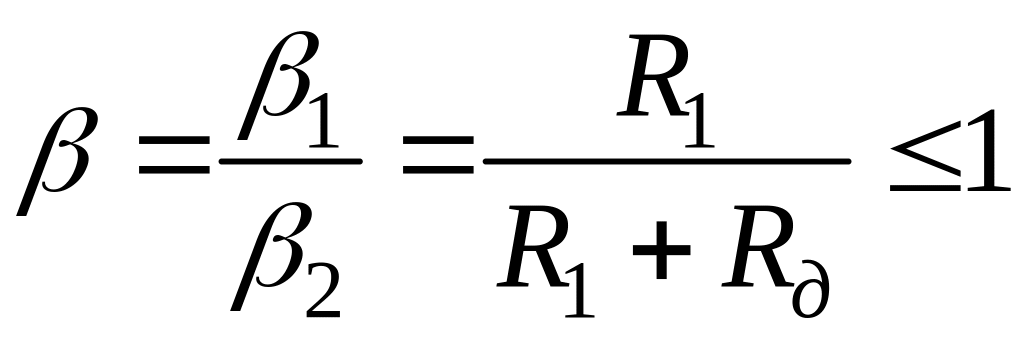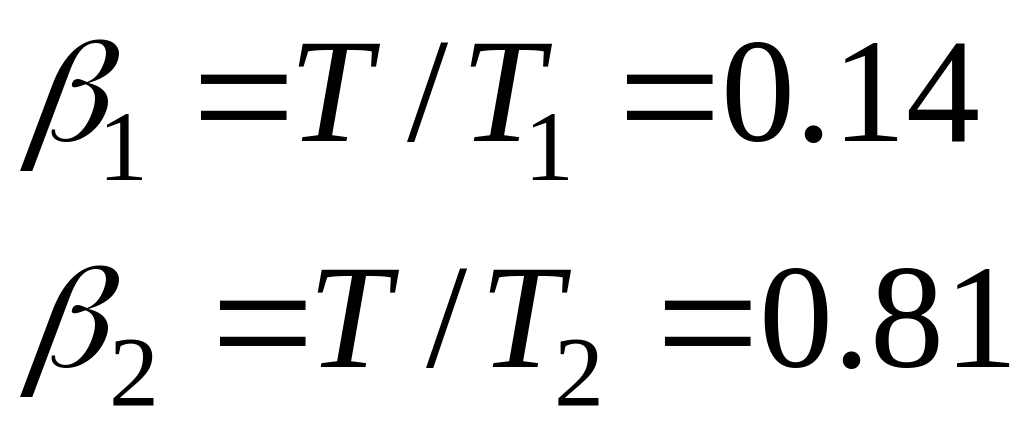
и - соответственно периоды коммутации в первом и втором интервалах времени в относительных единицах;

,

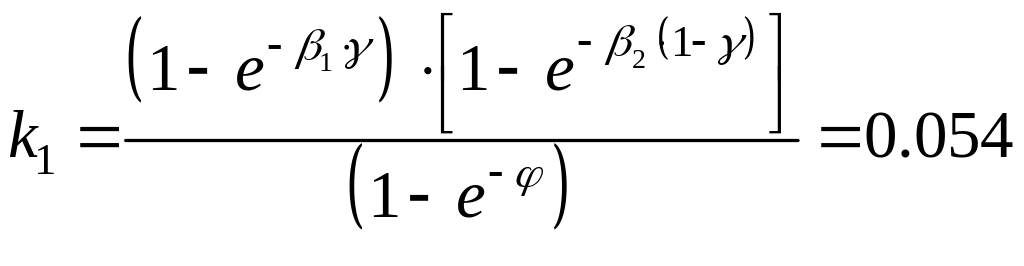где ,

- коэффициент пульсации постоянного тока.

Электромагнитный момент, развиваемый асинхронным электродвигателем в схеме с «импульсным» сопротивлением:

;

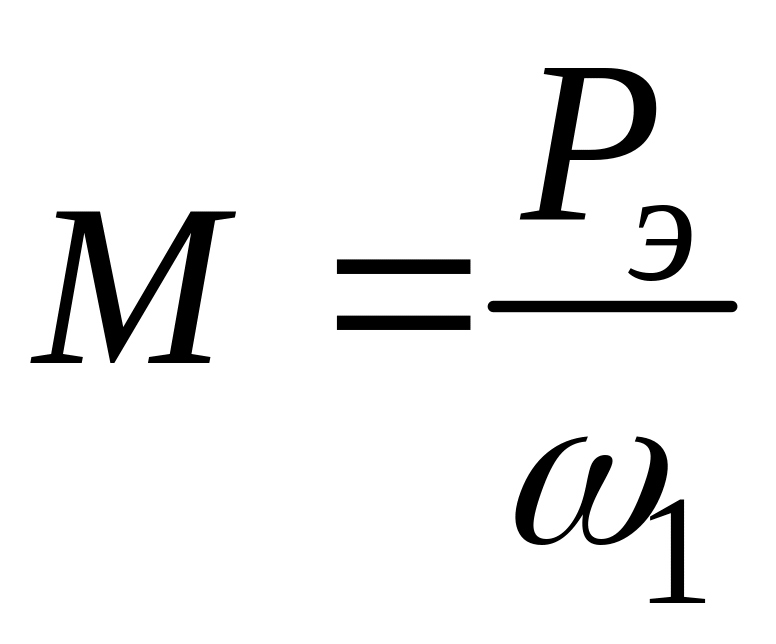Если пренебречь в первом приближении высшими гармониками тока ротора и пульсациями постоянного тока, то электромагнитная мощность асинхронного электродвигателя с выпрямителем в цепи ротора с точностью до 5% определяется равенством:

.

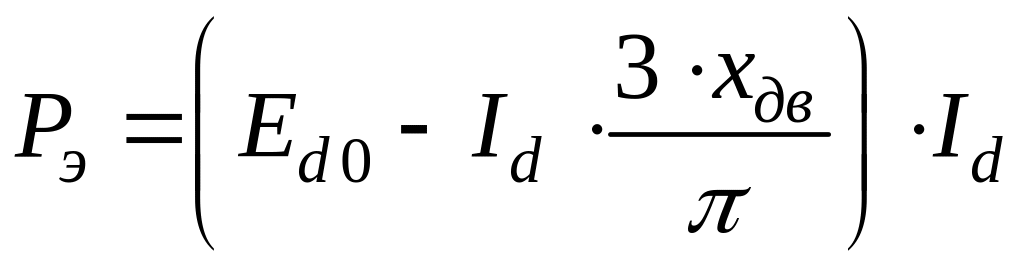Следовательно, электромагнитный момент двигателя:

Уравнение для среднего значения выпрямленного тока после подстановки значений

, , можно привести к виду:

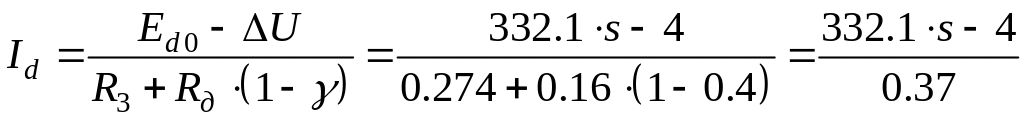
где

,

В свою очередь .

В случае применения полупроводниковых вентилей величиной можно пренебречь и считать .

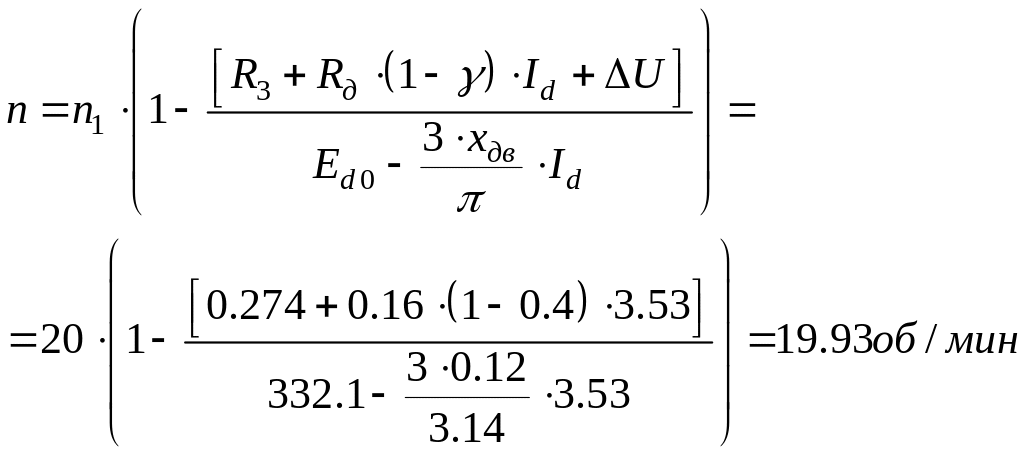
Достаточно простое выражение для механической характеристики можно получить, если пренебречь падением напряжения вследствие явления перекрытия вентилей.

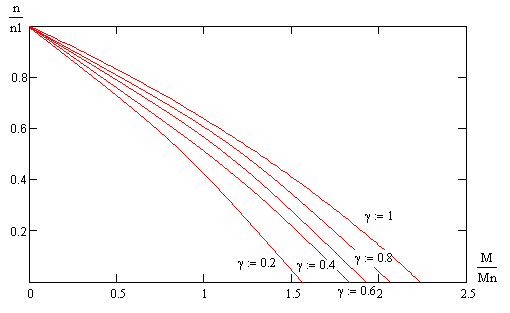
Рисунок 10. Механические характеристики импульсной системы электропривода.

Из рисунка видно, что механические характеристики рассматриваемой системы привода подобны механическим характеристикам при изменении активного сопротивления в цепи ротора асинхронного двигателя. Жесткость характеристик уменьшается при уменьшении скважности.