Вопрос 14 Строгая квантово-механическая теория атома водорода.
Вопрос16 Тонкая структура спектров, спин, теория Дирака.
Спин ядра. Спины нуклонов складываются в результирующий спин ядра. Спин нуклона равен 1/2. Поэтому квантовое число спина ядра I будет полуцелым при нечетном числе нуклонов А и целым или нулем при четном А. Спины ядер I не превышают нескольких единиц. Это указывает на то, что спины большинства нуклонов в ядре взаимно компенсируют друг друга, располагаясь антипараллельно.
Механический
момент ядра
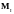складывается с моментом электронной
оболочки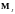
в
полный момент импульса атома
,
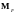который определяется квантовым числом
F.
Взаимодействие магнитных моментов электронов и ядра приводит к тому, что состояния атома, соответствующие различным взаимным ориентациям и (т.е. различным F), имеют немного отличающуюся энергию. Как уже говорилось раньше, взаимодействием L и S обуславливается тонкая структура спектров. Взаимодействием I и J определяется сверхтонкая структура атомных спектров. Расщепление линий, соответствующее сверхтонкой структуре, порядка нескольких сотен ангстрема.
Основы теории Дебая.
Дебай учёл, что колебания атомов в кристаллической решётке не являются независимыми.
Число
стоячих волн, приходящихся на единицу
объёма кристалла, т.е. нормальных
колебаний, частоты которых заключены
в интервале от
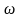до
,
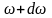равно
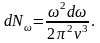(1.10)
где v-фазовая скорость волны в кристалле.
Однако эта формула не учитывает возможных видов поляризации волны. В твёрдой среде вдоль некоторого направления могут распространяться три разные волны с одним и тем же значением частоты , различающиеся направлением поляризации; одна продольная и две поперечные с взаимно перпендикулярными направлениями колебаний. В соответствии с этим формула (1.10) может быть изменена следующим образом
.
здесь
-
фазовая скорость продольных, а
-
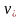поперечных упругих волн. Положим для
простоты, что
=
=
v.
Тогда
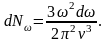(1.11)
Максимальную
частоту
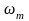нормальных
колебаний решётки можно найти, приравняв
полное число колебаний числу степеней
свободы, равному 3n
(n-
число атомов в единице объёма кристалла)
Отсюда
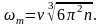(1.12)
Наименьшая длина волны возбуждаемая в кристалле, оказывается равной
,
где d- расстояние между соседними атомами в решётке, Этот результат согласуется с тем, что волны, длина которых меньше удвоенного межатомного расстояния, не имеют физического смысла. Исключив из (1.11) и (1.12) скорость, получим
.
(1.13)
Внутренняя энергия единицы объёма может быть представлена в виде
,
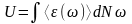где
-
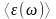среднее значение энергии нормального
колебания частоты
.
Подставляя сюда выражение
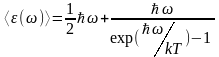и (1.13) получаем
,
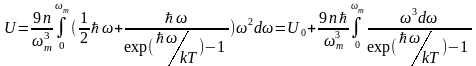где
-
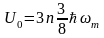энергия нулевых колебаний кристалла.
Производная
-
даёт теплоёмкость кристалла
.
(1.14)
Величину
,
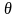определяемую условием
,
называют характеристической
температурой Дебая.
.
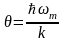(1.15)
Температура Дебая указывает для каждого вещества ту область, где становится существенным квантование энергии колебаний, Зависимость теплоёмкости С от Т показана на рис.1.5.
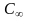-классическое
значение теплоёмкости, получающееся
из квантовых формул при Т=0.
Формула
Дебая хорошо передает ход теплоёмкости
с температурой для тел с простыми
кристаллическими решётками. К более
сложной структуре кристаллов формула
Дебая не применима. Это объясняется
тем, что у таких тел спектр колебаний
оказывается очень сложным, В рассмотренном
случае с одним атомом в кристаллической
ячейке, каждому значению волнового
вектора
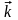соответствовали3
значения
(одна продольная и две поперечные волны).
Если число атомов в элементарной ячейке
кристалла равно r, каждому значению
соответствует 3r различных частот;
следовательно, частота является
многозначной функцией волнового вектора,
обладающей 3r ветвями. Так для r = 2,т.е.
одномерной цепочки состоящей из
чередующихся атомов двух сортов,
зависимость wот
k
имеет вид, показанный на рис.1.6.
В трехмерном случае из 3r ветвей три являются акустическими, остальные – оптические. При нормальном колебании акустические частоты отвечают колебаниям атомов, помещающихся в различных элементарных ячейках, относительно друг друга, Оптические частоты – колебаниям атомов относительно друг друга в элементарной ячейке.