Вопрос 8. Уравнение Шредингера. Решение для свободной частицы.
В квантовой механике уравнение Шредингера играет фундаментальную роль. Оно позволяет найти вид волновой функции частиц, движущихся в различных силовых полях. Вид волновой функции или -функции получается из решения уравнения, которое выглядит следующим образом
. 
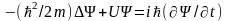(12.1)
Здесь m – масса частицы; i – мнимая единица; – оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых производных по координатам
.
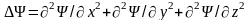Буквой U в уравнении (12.1) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу.
Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено из других уравнений. Если силовое поле, в котором движется частица, стационарно (т.е. постоянно во времени), то функция U не зависит от времени и имеет смысл потенциальной энергии. В этом случае решение уравнения Шредингера состоит из двух множителей, один из которых зависит только от координат, другой – только от времени
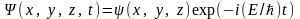. (12.2)
Здесь Е –
полная энергия частицы, которая в случае
стационарного поля остается постоянной;
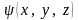– координатная часть волновой функции.
Чтобы убедиться в справедливости (12.2),
подставим его в (12.1)
В результате получим
. (12.3)
Уравнение (12.3) называется уравнением Шредингера для стационарных состояний.Уравнение (12.3) часто записывают в виде
.
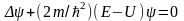Под оператором
подразумевается правило, посредством
которого одной функции, обозначим ее
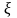сопоставляется другая функция, обозначим
ее f.
,
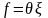Если рассматривать
функцию U в уравнении (12.3) как оператор,
действие которого на -функцию
сводится к умножению
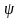на U, то уравнение (12.3) можно записать
так:
. (12.4)
В этом уравнении
символом
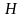обозначен оператор, равный сумме
операторов
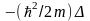и U:
.
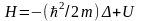Оператор оператором Гамильтона.Гамильтониан является оператором энергии Е. В квантовой механике другим физическим величинам также сопоставляются операторы
В разд. 10 мы уже обсуждали физический смысл -функции: квадрат модуля -функции определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:
, (12.5)
Тогда вероятность обнаружения частицы в объеме V
.
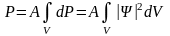Для одномерного случая
.
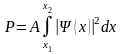Интеграл
от выражения (12.5), взятый по всему
пространству от
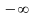до
,
равняется единице:
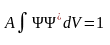
Действительно, этот интеграл дает вероятность того, что частица находится в одной из точек пространства, т. е. вероятность достоверного события, которая равна 1.
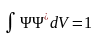(12.6)
Условие (12.6) называется условием нормировки. Функции, удовлетворяющие этому условию, называются нормированными. В случае стационарного силового поля справедливо соотношение
,
т. е. плотность вероятности волновой функции равна плотности вероятности координатной части волновой функции и от времени не зависит.
Свойства -функции: она должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек) и иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий.
В уравнение Шредингера в качестве параметра входит полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида имеют решения, удовлетворяющие стандартным условиям, не при любых, а лишь при некоторых определенных значениях параметра (т. е. энергии Е). Эти значения называются собственными значениями. Решения, соответствующие собственным значениям, называются собственными функциями.