13. Дифференциальное исчисление функций нескольких переменных

13.1. Предел и непрерывность функции нескольких переменных

Если каждой паре значений двух независимых друг от друга переменных из области ставится в соответствие единственное вещественное значение , то это соответствие называется функцией двух переменных.

Окрестностью точки (или -окрестностью) называется множество всех точек плоскости, координаты которых удовлетворяют неравенству . То есть

-окрестность – это внутренние точки круга с центром и радиусом .

Число А называется пределом функции при (то есть при и )

А= =

если для любого найдётся такое, что для всех точек М из -окрестности (за исключением, возможно, самой точки ) выполняется неравенство . Если предел существует, то он не зависит от пути, по которому М стремится к .

Функция называется непрерывной в точке М , т.е. при , если она определена в окрестности этой точки и .

13.2. Частные производные

Частной производной по переменной х от функции называется предел отношения частного приращения этой функции по переменной х к этому приращению, когда последнее стремится к нулю:

_.

_{Частная производная по х есть обычная производная от функции} , которая рассматривается как функция только от переменной х, при фиксированном значении переменной у.

Аналогично можно определить производную по переменной у:

_.

Пример. Найти , если .

Решение. Т.к. производная по переменной х вычисляется при неизменном y, то = . Аналогично .

Функции , называют частными производными первого порядка.

Эти функции тоже могут иметь частные производные, которые называются частными производными второго порядка. Они обозначаются следующим образом: = , , ,

.

Пример. Найти частные производные второго порядка функции .

Решение. Так как , и , то ,

, , .

Заметим, что . Это равенство всегда выполняется, если частные производные второго порядка непрерывны.

13.3. Дифференциал

Назовем величину полным приращением функции . Если полное приращение представимо в виде

,

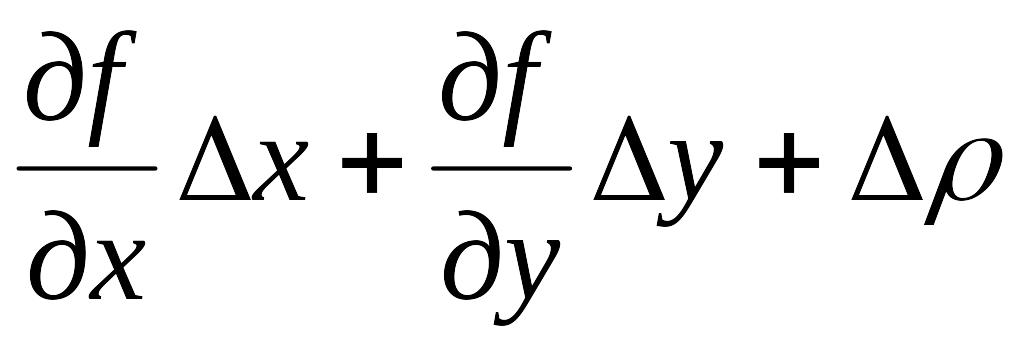где 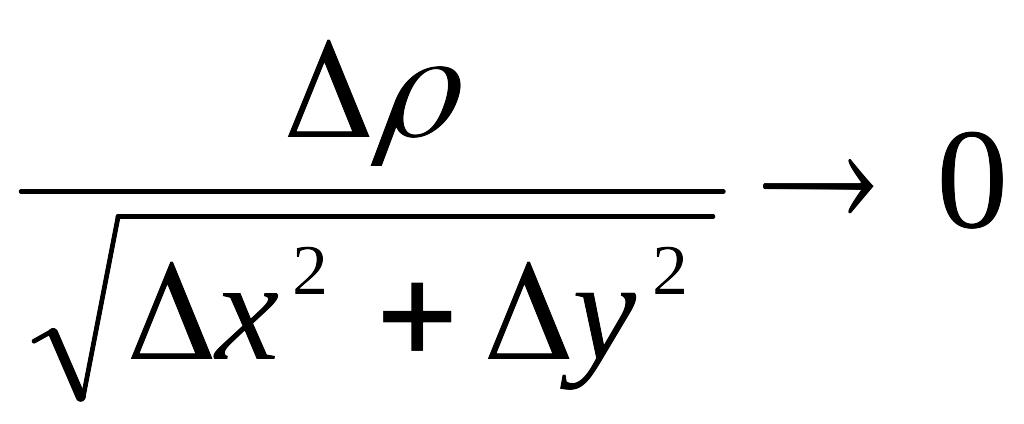, при , то функция называется дифференцируемой, а величина

=

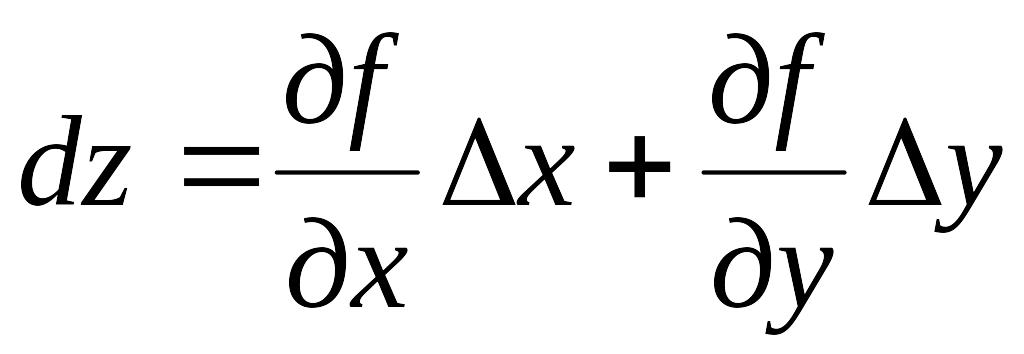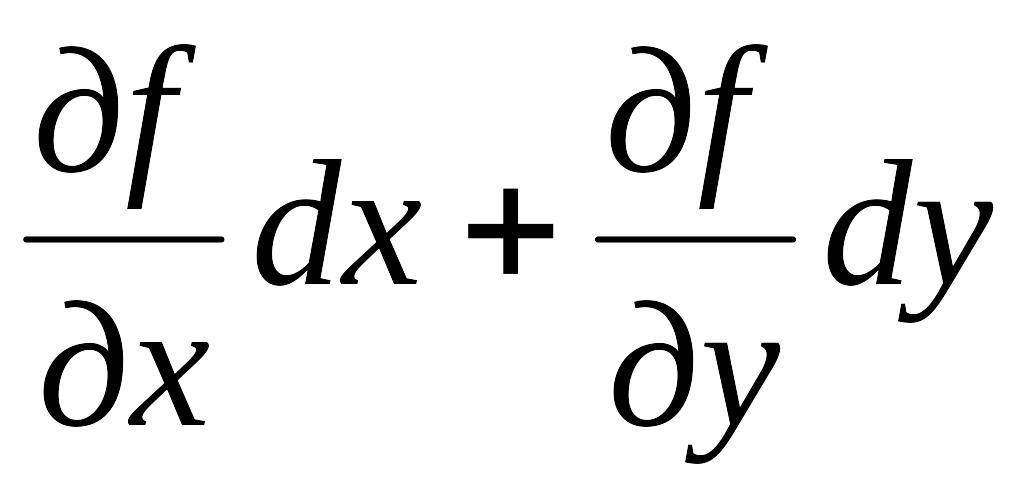
называется полным дифференциалом (приращения и обозначаются как и ).

Пример. Найти полный дифференциал функции .

Решение. Частные производные равны , , поэтому полный дифференциал равен .

13.4. Экстремумы функций нескольких переменных

Говорят, что функция   имеет локальный максимум в точке  , т.е. при , если  для всех точек , достаточно близких к точке  (т.е. лежащих в некоторой её окрестности) и отличных от неё.

Говорят, что функция   имеет локальный минимум в точке  , т.е. при , если  для всех точек , достаточно близких к точке  и отличных от неё.

(Слово «локальный» мы, далее, будем опускать). Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция  достигает экстремума при , то каждая частная производная первого порядка от  или обращается в ноль при этих значениях аргументов, или не существует.

Точки в которых частная производная первого порядка обращается в ноль называются стационарными.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку   , функция имеет непрерывные частные производные до второго порядка включительно. Пусть, кроме того, точка   является стационарной точкой функции , т.е. . Обозначим , где Тогда при  : 1)  имеет максимум, если   и . 2)  имеет минимум, если и . 3)   не имеет ни минимума, ни максимума, если . 4) если  , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

Пример. Найти экстремум функции .

  Решение. Сначала найдем частные производные:

, .

Стационарные точки найдем из системы уравнений:

Система имеет два решения: и . Значит, имеются две стационарные точки – это и .

Находим производные второго порядка данной функции:

,

В точке имеем Так как , то в этой точке экстремума нет.

В точке имеем Так как, и А>0, то функция в этой точке имеет минимум.