
Учебники и учебные пособия / Информационный анализ и автоматизированное проектирование станций биохимической очистки. Учебное пособие
.pdf
|
|
|
|
|
|
|
|
dw |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.. |
|
.. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0,5 |
|
|
|
|
|
|
|
|
|
.. |
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
. |
|
α 1 |
|
|
tgtg |
α1 = k5 |
|
|||||||
0,2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0,1 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,2 |
|
d0,4 |
|
|
0,6 |
|
|
0,8 |
|
1,0 |
|
|||||||||
-0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
k 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
-0,2 |
|
|
|
|
|
|
[ |
|
R d |
|
|
d |
d |
|
|
d |
|
|
] |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
___ |
|
R |
( |
Y33 |
|
- Y |
) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
V |
d |
(Y 1,0d −Y d1) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
Y dd
d |
d |
k |
d |
, |
k |
d |
Рис. 4.10 Определение констант |
4 |
5 |
||||
Рис. 4.10 Определение констант k4 |
, k5 |
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
.. . |
. |
. |
. |
|
k 2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
. α 2 |
|
|
|
|
d |
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
tg |
α2 = |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
d |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
____ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
k d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
2 |
|
|
4 |
|
|
6 |
|
8 |
d |
10 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[( |
|
d |
|
-k |
] |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 3 |
) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
d |
d |
k d , |
k d |
|
|
|
|
|
|
|||||
|
|
|
|
Рис. 4..114.11ОпределОпределениеконстантконстантk , k , |
kk d , |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
7 |
|
|
|
|
|
|
|
|||||
что k d |
известно, то k d , k d |
7 |
|
|
|
|
|
|
|
|
|
|
|
основан |
|||||||||||||||
находятся так же, как и другие константы. Поиск k d , а затем и k d , k d |
|||||||||||||||||||||||||||||
7 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
1 |
2 |
|
|||||
на сканировании всего диапазона изменения k7d (k7d [0, 1]) с некоторым шагом ∆k . Наиболее эффективен
в данном случае метод наименьших квадратов, позволяющий с большой точностью получать коэффициенты прямых, аппроксимирующих экспериментальные данные. Расчет коэффициентов проиллюстрирован на рис. 4.9 – 4.11.
В результате исследования математической модели (4.2) – (4.4) кинетики процесса денитрификации активным илом были получены следующие кинетические константы: k5d = 0,834 ; k4d = 0,217 сут−1 ;
k1d =1,256 сут−1 ; k2d = 0,196 ; k7d = 0,625 ; k6d = 0,306 ; k3d = 0,003 сут−1 .
4.4 Моделирование работы системы аварийной защиты и управления станцией биохимической очистки сочных вод
Подход к разработке системы автоматической аварийной защиты станции БХО, рассмотренный в разделе 3.4, проверим на модели станции, в составе которой «аэротенк – вторичный отстойник» с характеристиками, показанными в табл. 4.6.
4.6 Характеристики подсистемы

«аэротенк – вторичный отстойник»
|
ЕДИНИ- |
КОЛИ- |
|
НАИМЕНОВАНИЕ |
ЦА |
||
ИЗМЕРЕ- |
ЧЕСТВО |
||
|
|||
|
НИЯ |
|
|
|
|
|
|
Количество коридоров аэротен- |
– |
3 |
|
ка |
|
|
|
Длина аэротенка |
м |
45 |
|
|
|
|
|
Ширина коридора аэротенка |
м |
4,5 |
|
|
|
|
|
Высота аэротенка |
м |
5 |
|
|
|
|
|
Число ячеек в коридоре (при |
|
|
|
использовании ячеечной моде- |
– |
3 |
|
ли) |
|
|
|
Радиус вторичного отстойника |
м |
10 |
|
|
|
|
|
Высота вторичного отстойника |
м |
3 |
|
|
|
|
|
Входной расход воды |
м3/сут |
12 500 |
Результаты решения задач А-I и А-II для станции приведены на рис. 4.12 – 4.15. В частности на рис. 4.13 показана ситуация «срыва» статического режима работы станции БХО, возникшая по причине ступенчатого изменения Y1,0 , Y7,0 , Y4,0 . С помощью оптимальных управляющих воздействий
p* = 0,26, u* = 2048,3 м3/ч, являющихся решением задачи А-I, оказывается возможным «заблокировать» дей-
ствие аварийных возмущений. При этом, Y ** = 2,51 мг/л, Θ |
ила |
Θ [7,5 ... 9,5]= 9,3. |
2 |
|
На рис. 4.14 изображена диаграмма подстройки параметров модели под новый кислородный режим в аэротенке, характеризуемый значением Y2** . Действие случайных факторов в объекте управления имитиро-
валось с помощью датчика случайных чисел εt N (0, 1), |
t =1, 2, 3, ... . Из этой диаграммы следует, что в слу- |
|
чае выбора значений dt = 30 c , новые оценки вектора |
~ |
могут быть найдены за 8 – 10 интервалов дис- |
λ(t) |
||
кретностей, или примерно за 5 минут. Такое время идентификации параметров модели (3.78) оказывается приемлемым для последующего решения задачи А-II в подсистеме стабилизации.
На рис. 4.15 изображен процесс управления кислородным режимом в аэротенке. Он сводится к определению таких значений u0 (t), t = 0, 1, 2, ... , при которых удается скомпенсировать отрицательные воз-
действия случайных факторов εt .
Предложенная система аварийной защиты может найти широкое применение на станции БХО, обслуживающей ПТС. В этом случае упрощается задача оперативной диагностики возмущений и оценки их влияния на работу подсистемы «аэротенк – вторичный отстойник».
4.5 Моделирование процессов самоочищения реки с малым расходом воды
Методику исследования природного водоема проиллюстрируем на примере реки Цны, как приемника очищенных сточных вод промышленных предприятий г. Тамбова, в том числе и ОАО «Пигмент».
Анализ процессов самоочищения воды реки проводился на участке реки длиной 60 км, начиная от точки сброса очищенных сточных вод с очистных сооружений ОАО «Пигмент» до ТроицкоДубравского гидроузла (рис. 4.16). Река Цна по классификации Огиевского относится к 3-й категории и имеет хозяйственно-питьевое назначение.

, мг/л |
3 |
2 |
|
Y |
|
 2
2 
1
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
номерячейки |
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 4.12 Изменениеконцентрациирастворенногокислородаподлине. 4 . 1 2 1-го- 3-гокоридоров
Y1 Y 4 Y 3 Y 6 Y 5 Y 2
Y1
60 |
|
30 |
|
4 |
|
8 |
|
30 |
|
6,0 |
|
|
|
|
|
Y6 |
|
|
|
Y 4 |
|
||||
|
|
|||
Y5 |
|
|
|
|
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
15 |
|
2 |
4 |
|
15 |
|
3,0 |
|
|
|
Y3 

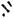



Y2
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
*10 |
3 |
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|||||||||
|
|
|
|
|
|
|
|
|
|
Y7, мг/л |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
мг/л |
|
|
|
|
|
|
|
|
Рис. 4.13 Иллюстрация срыва процесса биохимической очистки в результате ступенчатого изменения концентрации ингибитора во входном потоке

3 |
|
|
|
|
|
|
|
|
|
2, |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
число циклов |
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 4.14 |
Диаграмма подстройки параметров модели |
|
|
||||
|
. 4 . 1 4 - |
|
|||||||
|
3 |
|
|
|
|
|
|
|
|
2.5 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U(0) |
|
|
|
|
|
|
|
U |
|
III |
|
/ |
|
|
|
U(0) |
|
|
|
|
|
3 |
|
3 |
|
|
II |
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 10 |
|
|
|
|
|
|
|
|
|
1.5 10 |
3 |
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
II |
|
III |
|
|
|
Режим нормаль- |
Режим идентификации |
Режим стабили- |
|||||
|
|
ной эксплуатации |
параметров модели |
|
зации |
|
|||
1 10 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
|
|
||||||||
|
|
|
|
|
|
число циклов |
|
||
Рис. 4.15 Диаграмма изменения управляемых воздействий
Для исследуемого участка характерно следующее: среднегодовой расход – 12,3 м3/с, русло умеренно извилистое шириной 45 … 60 м, песчано-илистое, деформирующееся, незначительно заросшее водной растительностью. Прилагаемая местность – наклонная равнина, по левобережью открытая, по правобережью поросшая лесом. По берегам реки расположены населенные пункты, местные водозаборы, садово-огородные общества, использующие воду, зоны отдыха трудящихся. В связи с тем, что на участке имеются два гидроузла и несколько притоков, при моделировании разобьем его на 6 участков с относительно постоянными гидрохимическими параметрами. Схематично они изображены на рис. 4.16.
В результате исследования процессов, протекающих в реке, были выделены процессы аэробного окисления органики, нитрификации, денитрификации, роста и отмирания планктона, деаэрации воды кислородом воздуха, аммонификации белка и мочевины, ионного обмена и другие. В качестве «кандидата» модели для проведения имитационного испытания использована модель (3.47) – (3.61).
Формирование ограничений на выходные переменные модели вида (3.7) – (3.10) и определение диапазонов изменения начальных состояний и внешних воздействий (смывы органики с полей) осуществлялись на основе информации Центрально-Черноземной региональной, городской и заводской (ОАО «Пигмент») гидрохимических лабораторий с учетом полевых измерений концентраций аммонийного и нитратного азота, а также растворенного кислорода в сечениях А, Б, В, выполненных с помощью передвижной лаборатории контроля качества поверхностных вод. В тех случаях, когда информация носила качественный характер, ее преобразование в количественную форму осуществлялось с помощью фор-

мул (3.11) – (3.15). Часть ограничений (3.7) – (3.10) проиллюстрирована на рис. 4.16 и 4.17.
При решении системы уравнений модели в ходе имитационного испытания суммарный интервал времени для всего участка длиной 60 км составил 10 дней. Значения коэффициентов модели выбирались из диапазонов их «правдоподобных» значений. На рис. 4.18, а начальные диапазоны изменения коэффициентов отмечены под числовой осью. Характер изменения выходных переменных при определенных значениях коэффициентов и начальных условий (см. табл. 4.7) приведен на рис. 4.17. При отыскании «правдоподобных» диапазонов коэффициентов было выполнено несколько пробных серий решений системы уравнений. На рис. 4.18, а для коэффициента штриховкой под числовой осью отмечен «правдоподобный» диапазон. «Допустимые» реакции с значениями в пределах него образуют пустое множество.
|
|
Дубрава |
|
|
60 км |
|
|
В |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Троицкая |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
56 км |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Горелое |
|
|
50 км |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
___ |
S=1,s |
|
|
ТихийУгол |
|
|
___ |
L=1,l, |
|||||||||
|
|
|
|
||||||||||||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полейс |
,=1,7i |
|
|
|
км36 |
|
|
|
|
** ,li |
|||||||
___ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
___ |
i=1,7 |
|
Смывы |
Y<0 |
Татаново Куксово |
км21 |
Б |
|
контроляПосты качестваводы |
|
, |
|||||||||
|
|
Y |
|||||||||||||||
органики r s i, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
** i,s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r ,li |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* i,l |
|
|
|
Донское |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
7 км |
|
|
|
вод |
=1,7i |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
___ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сточных |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
** ,0 i |
|
|
|
|
|
Тамбов.г |
|
|
|
|
|
|
|
|
|
Точкасброса очищенных |
, |
|
|
||
|
|
|
|
|
|
|
|
|
|
А |
Y |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 0 i, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* i,0 |
|
|
|
Рис. 4.16 Схема участка реки Цны Рис. 4.16 СхемаучасткарекиЦны

Y r, мг/л
12
10
8
6
4
2
0
0 |
2 |
4 |
6 |
8 |
10 |
|
|
|
|
t, |
дни |
|
|
|
|
|
|
|
||
Рис. 4.17 Характер изменения выходных переменных модели:
––– – – –– ПК; –– – –– азот органических соединений; – – – – аммонийный азот;
––– – –– нитратный азот; – – – – растворенный кислород; –– –– хром;
––––– фосфор; ––––– четкие ограничения; |
нечеткие ограничения |
Для окончательного выяснения диапазонов изменения коэффициентов было проведено 9300 решений системы уравнений, в 10 % из них получены решения, удовлетворяющие ограничениям. В табл. 4.7 приведены диапазоны изменения всех коэффициентов модели, а на рис. 4.18, а – коэффициентов, показанные штриховкой над числовой осью. Из этого рисунка видно, что для одних коэффициентов «допустимые» реакции получены во всем предполагаемом диапазоне, для других – он был назначен с большим «запасом».
Все семейство кривых изменения во времени образует некоторую область. На рис. 4.19 изображены области изменения концентраций растворенного кислорода для всех реакций модели и реакций, удовлетворяющих ограничениям, а также гистограммы. На рис. 4.18, б показаны гистограммы значений отдельных коэффициентов для «допустимых» реакций модели.
В результате проведения имитационного испытания была создана математическая модель исследуемого участка реки Цны, удовлетворяющая всем имеющимся экспериментальным данным. Затраты машинного времени на идентификацию модели с быстродействием ПЭВМ 106 оп/с составили менее двух часов. Для проверки адекватности в июне 1990 года были проведены расчеты по модели и полевые измерения состояния качества воды (концентраций органического, нитратного, аммонийного азота, растворенного кислорода) в сечениях А, Б, В участка реки. Оказалось, что все концентрации, рассчитанные по модели, попадают в 95 %-ный доверительный интервал. При этом, максимальная относительная ошибка по нитратному, аммонийному азоту и растворенному кислороду не превышает 10 %, органическому азоту – 15,8 %.
На заключительном этапе исследования участка реки Цны были выполнены прогнозы содержания в воде растворенного кислорода и примесей в зависимости от степени очистки стоков в сечении А на основе следующего правила:

если
Y r |
|
=Y r,зад Y r |
=Y r,зад |
|
16 |
|
|
|
|
|
|
|
|
|
1,i0 |
2,i0 |
2,i0 |
|
|
(k j = {k j [k j , k j |
], v =1, N}) T =T , |
||||
1,i0 |
|
|
v |
н в |
|
|
зад |
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
r |
r,зад |
|
|
|
|
|
|
|
|
|
... |
Y7,i0 =Y7,i0 |
|
|
j =1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то
ˆ |
r |
r,lim |
|
|
|
|
i |
|
ˆ |
r |
|
|
r,lim |
|
i |
ˆ |
r |
|
r,lim |
|
|
|
i |
|
|
|
{P (Y1,i ≤ Y1,i |
)≥ δY1,i P (Y2,i ≤ Y2,i |
|
)≥ δY2,i |
P (Y3,i ≤ Y3,i |
)≥ δY3,i |
|
||||||||||||||||||||
ˆ |
r |
r,lim |
|
|
|
i |
|
|
ˆ |
r |
r,lim |
i |
ˆ |
r |
|
r,lim |
|
|
i |
|
|
|||||
P (Y4,i ≤ Y4,i |
|
)≥ δY4,i |
P (Y5,i ≥ Y5,i |
|
)≥ δY1,i P (Y6,i ≤ Y6,i |
|
)≥ δY1,i |
|||||||||||||||||||
ˆ |
r |
r,lim |
|
|
|
i |
}, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P (Y1,i ≤ Y1,i |
|
)≥ δY1,i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
0,051 |
|
|
|
|
|
|
|
0,495 |
|
|
|
|
|
|
|
|
r |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k 1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
0,040 |
|
|
|
0,316 |
|
|
|
0,600 |
|
0,833 |
|
|
|
|
r |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0,300 |
|
|
|
|
|
0,950 |
|
|
|
|
|||||
0,110 |
0,899 |
r |
0 |
1 |
k 11 |
0,100 |
0,900 |
|
0,031 |
0,086 |
|
r |
0 |
0,090 |
1 |
k 14 |
0,030 |
0,900 |
|
|
|
|
a)а) |
|
|
|
|
|
|
|
|
|
0,051 |
r |
0,495 |
0,316 |
r |
0,833 |
||
|
k11 |
|
|
|
k44 |
|
|
0,110 |
r |
0,899 |
|
|
|
|
|
|
|
0,031 |
r |
0,0.086 |
|||||
|
k 11 |
|
|
|
|
k 14 |
|
|
)б)
Рис. 4.18 Исходные данные и найденные в ходе испытания модели диапазоны изменения (а) и гистограммы (б) значений коэффициентов k1r , k4r , k11r , k14r

12
10
8
6
4
2
0
0
А
А
Область всех реакций
Область&"допустимых"» реакций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
t, дни |
|
|
|
10В |
|||||
|
|
)а) |
|
|
|
|
||||||
|
|
|
|
|
В |
|||||||
Всереакции |
|
|
|
|||||||||
|
Допустимые»" |
|
|
|
|
|
|
|
||||
" |
|
|
|
|
|
|
|
|||||
& |
реакции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
0,630 |
4,710 |
0,670 |
11,890 |
|
|
)б) |
|
|
|
|
|
Рис. 4.19 Области изменения (а) и гистограммы значений (б) |
||||||||
|
|
|
|
|
концентраций растворенного кислорода |
|||||||
где Y r,зад , Y r,зад , ..., Y r,зад , T зад |
– концентрации примесей, растворенного кислорода и температура в i-м |
|||||||||||
1,i0 |
2,i0 |
7,i0 |
|
|
|
|
|
|
|
|
||
створе реки, известные в момент прогноза t = 0 ; |
k нj , k вj – нижняя и верхняя границы изменения коэффици- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ента k v , v = |
1, N |
|
; P – вероятность; Y r,зад , |
Y r,зад , ..., |
Y r,зад , T зад – предельно допустимые значения концентра- |
|||||||
j |
|
|
|
1,i0 |
2,i0 |
|
|
7,i0 |
||||
ций веществ в речном потоке; |
δYi |
, δYi |
, ..., δYi |
|
– расчетные значения вероятностей; N – количество слу- |
|||||||
|
|
|
|
|
1,i |
|
2,i |
7,i |
|
|
|
|
чайных значений коэффициента k j . |
|
|
|
|
|
|||||||
|
|
|
|
4.7 Диапазоны изменения всех коэффициентов модели |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пара- |
|
|
|
Нижняя граница |
|
|
|
Верхняя граница |
||||
метр |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Начальные условия |
|
|
|
|
||||
Y1r,1 |
|
|
|
6,30 |
|
|
|
|
|
7,70 |
|
|
Y2r,1 |
|
|
|
10,80 |
|
|
|
|
13,20 |
|
||
Y3r,1 |
0,90 |
|
1,10 |
|
Y4r,1 |
33,60 |
|
4,40 |
|
Y5r,1 |
3,95 |
|
4,95 |
|
Y6r,1 |
0,18 |
|
0,23 |
|
Y7r,1 |
1,80 |
|
2,20 |
|
|
Коэффициенты |
|
|
|
k1r |
0,051 |
|
0,495 |
|
k2r |
0,106 |
|
0,682 |
|
k3r |
0,001 |
|
0,009 |
|
k4r |
0,316 |
|
0,830 |
|
k5r |
0,312 |
|
0,896 |
|
|
|
|
|
Продолжение табл. 4.7 |
|
|
|
|
|
|
|
|
|
|
Пара- |
Нижняя граница |
|
Верхняя граница |
|
метр |
|
|||
|
|
|
|
|
|
Начальные условия |
|
|
|
k6r |
0,087 |
|
0,595 |
|
k7r |
0,134 |
|
0,751 |
|
k8r |
0,022 |
|
0,099 |
|
k9r |
0,531 |
|
1,998 |
|
k10r |
0,735 |
|
2,667 |
|
k11r |
0,110 |
|
0,899 |
|
k12r |
0,006 |
|
0,495 |
|
k13r |
0,001 |
|
0,059 |
|
k14r |
0,031 |
|
0,086 |
|
k15r |
0,032 |
|
0,086 |
|
k16r |
0,110 |
|
0,660 |
|
|
Внешние воздействия |
|||
|
|
|
|
|
l1r,1 |
1,17 |
|
1,25 |
|
|
|
|
|
|
l2r,1 |
0,60 |
|
0,80 |
|
|
|
|
|
|
T |
19,00 |
|
23,00 |
|
Гистограммы прогнозируемых концентраций растворенного в воде кислорода приведены на рис. 4.20. Качество воды в контрольном створе реки Цны с вероятностью не менее 0,89 отвечает принятым нормам.

В
2
3
4 |
|
|
Б |
|
|
5 |
|
|
6 |
||
|
7 |
||
|
|
|
А |
Рис. 4.20 Гистограммы прогнозируемых значений концентрации растворенного кислорода
Рис. 4.20 Гистограммы прогнозируемых значений концентрации растворенного кислорода
