4. «Микроусловия бизнес-идеи» представляют из себя функцию от переменных, принимающих следующие значения:
Производственно-технологическая система
• очень хорошо соответствует бизнес-идее
• хорошо соответствует бизнес-идее
• неплохо соответствует бизнес-идее
• не совсем хорошо соответствует бизнес-идее
• плохо соответствует бизнес-идее
• очень плохо соответствует бизнес-идее
Финансово-экономическая система
• очень хорошо соответствует бизнес-идее
• хорошо соответствует бизнес-идее
• неплохо соответствует бизнес-идее
• не совсем хорошо соответствует бизнес-идее
• плохо соответствует бизнес-идее
• очень плохо соответствует бизнес-идее
Система управления
• очень хорошо соответствует бизнес-идее
• хорошо соответствует бизнес-идее
• неплохо соответствует бизнес-идее
• не совсем хорошо соответствует бизнес-идее
• плохо соответствует бизнес-идее
• очень плохо соответствует бизнес-идее
Система подготовки производства и маркетинга
• очень хорошо соответствует бизнес-идее
• хорошо соответствует бизнес-идее
• неплохо соответствует бизнес-идее
• не совсем хорошо соответствует бизнес-идее
• плохо соответствует бизнес-идее
• очень плохо соответствует бизнес-идее
Система корпоративной культуры
• очень хорошо соответствует бизнес-идее
• хорошо соответствует бизнес-идее
• неплохо соответствует бизнес-идее
• не совсем хорошо соответствует бизнес-идее
• плохо соответствует бизнес-идее
• очень плохо соответствует бизнес-идее
3.1.2. Координаты стратегических позиций
Покажем теперь, как составляется модель приближенных вычислений. На основе этой модели лежат последовательности нечетких высказываний. Пусть аi, bi, ci, di, ei, fi, gi, hi, 1i, mi, ni, oi, pi. qi, ri, si, ti, ui, wi (I = 1, 2, 3, :..) значения (нечеткие множества) лингвистических переменных, представленных выше, т.е. А, В, С, D, Е - переменные функции «рыночные условия»; F, Н, L, М - переменные функции «отраслевые условия»; N, О, Р, Q — переменные функции «макроусловия»; R, S, Т, U, W - переменные функции «микроусловия» с универсумами А, В, X, Δ, Е, Ф, Г, Н, I, К, Л, М, N, О, П, Θ, П, S, П соответственно.
Рассмотрим следующую нечеткую посылку (условное предложение) опирающуюся на переменные А, В, С, D, Е с результирующей переменной заключением Y:
Если А есть а1 И В есть b1 И С есть с1, И D есть d1
И Е есть е1, .
То Y есть у1
Если теперь переменные А, В, С, D, Е будут иметь значения а0, Ь0 с0, е0 то выводимое значение Уо результирующей переменной находится посредством применения композиционного правила Заде54:
μy0(ξ) = min(μy1(ξ); max(min(μa0(ά), μa0(ά))),
(min(μb0(β), μa0(β))),
(min(μc0(χ), μa0(χ))), (6)
(min(μd0(δ), μa0(δ))),
(min(μe0(ε), μa0(ε)))
Два или больше нечетких условных высказывания можно объединить связкой ИНАЧЕ, образуя нечеткие алгоритмы. Как показал Заде, связка ИНАЧЕ моделируется оператором так:
Если А есть а1 И В есть b1, И С есть с1 И D есть d1
И Е есть е1
То Y есть у1
ИНАЧЕ
Если А есть а2 И В есть b2, И С есть с2 И D есть d2
И Е есть е2 , '
То Y есть у2
Если теперь переменные А, В, С, D, Е, будут иметь значения а0, b0, c0, d0, е0, то выводимое значение y0 результирующей переменной можно вывести из уравнения:
μy0(ξ) = min(μy1(ξ); max(min(μa0(ά), μa1(ά))),
(min(μb0(β), μa1(β))),
(min(μc0(χ), μa1(χ))),
(min(μd0(δ), μa1(δ))),
(min(μe0(ε), μa1(ε))) (7)
μy0(ξ) = min(μy1(ξ); max(min(μa0(ά), μa2(ά))),
(min(μb0(β), μa2(β))),
(min(μc0(χ), μa2(χ))),
(min(μd0(δ), μa2(δ))),
(min(μe0(ε), μa2(ε)))
Очевидно, что для объединения более двух нечеткий утверждений потребуется лишь очевидное обобщение уравнения (7).
В результате решения нечеткого уравнения типа (7) будет получена функция принадлежности нечеткого множества значений лингвистической переменной решения. В качестве решения выбирается значение лингвистической переменной решения, при котором достигается тах исчисленной функции принадлежности.
Нечеткие множества значений лингвистических переменных можно определять различными способами. На практике очень хорошо зарекомендовал себя способ, при котором для такого определения используются экспоненциальные функции. Например, для определения значения, соответствующего большому положительному результату, используется функция (8):
(8)
Значения положительного результата, определяются функцией (9):
(9)
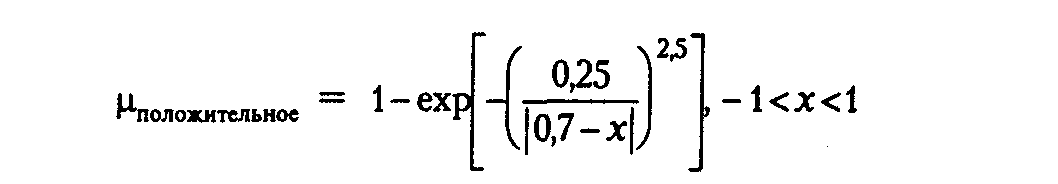
Значения неотрицательного результата определяются функцией (10): (10)
Значения неположительного результата определяются функцией (II):
(11)
Значения отрицательного результата определяются функцией (12):
(12)
Значения большого отрицательного результата определяются функцией (13):
(13)
В отношении конкретных лингвистических переменных термы, соответствующие функциям, определенным в формулах (8) - (13), подменяются на подходящие в каждом конкретном случае. Скажем, если идет речь об определении значения переменной «производственно-технологическая система» как отдельной лингвистической переменной, то терм большое положительное значение будем заменяться термом очень хорошо соответствует бизнес-идее. Однако смысл выражаемый данным термом, а также функция принадлежности при этом не изменятся.
Графики функций, описанных выражениями (8) — (13), приведены на рис. 23.