Вопрос 13: Квантовый линейный гармонический осциллятор

Н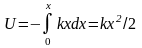 а рис. 18.1, а изображен классический гармонический осциллятор в виде шарика массой m, подвешенного на пружине с коэффициентом жесткости k. Сила, действующая на шарик и ответственная за его колебания, связана с координатой х формулой . Потенциальная энергия шарика есть

Рис. 18.1

Е сли шарик вывести из положения равновесия, то он совершает колеба­ния с частотой . Зависимость потенциальной энергии от координа­ты х показана на рис. 18.1, б.

Уравнение Шредингера для гармонического осциллятора имеет вид

Решение этого уравнения приводит к квантованию энергии осциллятора. Собственные значения энергии осциллятора определяются выражением

Как и в случае потенциальной ямы с бесконечно высокими стенками, минимальная энергия осциллятора отлична от нуля. Наименьшее возможное значение энергии при n = 0 называют энергией нулевых колебаний. Для классического гармонического осциллятора в точке с координатой x = 0 энергия равна нулю. Существование энергии нулевых колебаний подтверждается экспериментами по изучению рассеяния света кристаллами при низких температурах. Спектр энергий частицы оказывается эквидистантным, т. е. расстояние между уровнями энергии равно энергии колебаний классического осциллятора

Приведем (без вывода) выражения для нескольких первых собственных функций гармонического осциллятора:

Графики для соответствующих плотностей вероятности изображены на рис. 18.2. Границы «классической» траектории осциллятора помечены как и .

Рис. 18.2

График «классической» плотности вероятности изображен на рис. 18.3 пунктирной кривой. Видно, что, как и в случае потенциальной ямы, поведение квантового осциллятора существенным образом отличается от поведения классического.

В

Рис. 18.3

ероятность для классического осциллятора всегда максимальна вблизи точек поворота, а для квантового осциллятора вероятность максимальна в пучностях собственных -функций. К тому же квантовая вероятность оказывается отличной от нуля и за точками поворота, ограничивающими движение классического осциллятора.

На примере квантового осциллятора опять прослеживается упоминавшийся ранее принцип соответствия. На рис. 18.3 изображены графики для классической и квантовой плотностей вероятности при большом квантовом числе n. Хорошо видно, что усреднение квантовой кривой приводит к классическому результату.

Вопрос 16 Тонкая структура спектров, спин, теория Дирака.

Спин ядра. Спины нуклонов складываются в результирующий спин ядра. Спин нуклона равен 1/2. Поэтому квантовое число спина ядра I будет полуцелым при нечетном числе нуклонов А и целым или нулем при четном А. Спины ядер I не превышают нескольких единиц. Это указывает на то, что спины большинства нуклонов в ядре взаимно компенсируют друг друга, располагаясь антипараллельно.

Механический момент ядра складывается с моментом электронной оболочки в полный момент импульса атома , который определяется квантовым числом F.

Взаимодействие магнитных моментов электронов и ядра приводит к тому, что состояния атома, соответствующие различным взаимным ориентациям и (т.е. различным F), имеют немного отличающуюся энергию. Как уже говорилось раньше, взаимодействием _L и _S обуславливается тонкая структура спектров. Взаимодействием _I и _J определяется сверхтонкая структура атомных спектров. Расщепление линий, соответствующее сверхтонкой структуре, порядка нескольких сотен ангстрема. Структура спектра, отражающая расщипление линий на компоненты наз. тонкой структурой. Ур-е Дирака