Вопрос 26 Квазиклассическая волновая функция. Квантование Бора-Зоммерфельда. Нахождение уровней энергии одномерного потенциального ящика, атома водорода.

Квазиклассическое приближение,— самый известный пример квазиклассического вычисления в квантовой механике, в котором волновая функция представлена как показательная функция, квазиклассически расширенная, а затем или амплитуда, или фаза медленно изменяются

+фото в телефоне

Вопрос 27: Излучение и поглощение квантов света. Ширина спектральной линии

Излучение и поглощение электромагнитных волн происходит порциями, квантами, однако процессы распространения волны непрерывны. Квантовый характер явлений излучения и поглощения доказывает наличие у микросистем, в том числе у электромагнитного поля, отдельных энергетических уровней и невозможность микросистемы обладать произвольной величиной энергии. Корпускулярные представления хорошо согласуются с экспериментально наблюдаемыми закономерностями излучения и поглощения электромагнитных волн, в частности, с закономерностями теплового излучения и фотоэффекта. Однако по их мнению экспериментальные данные свидетельствуют, что квантовые свойства электромагнитной волны не проявляются при распространении, рассеянии, дифракции электромагнитных волн, если они не сопровождаются потерей энергии. В процессах распространения электромагнитная волна не локализована в определённой точке пространства, ведёт себя как единое целое и описывается уравнениями Максвелла. Решение было найдено в рамках квантовой электродинамики и её преемницы Стандартной модели.

Ширина спектральных линий -  интервал частот v (или длин волн λ = c/ν, с — скорость света), характеризующий спектральные линии в спектрах оптических атомов, молекул и др. квантовых систем. Каждому излучательному квантовому переходу между дискретными уровнями энергии E_k и E_i соответствует некоторый интервал Δν_ki частот, близких к частоте перехода 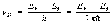 — Планка постоянная). Значение Δν_ki определяет Ш. с. л. ― степень немонохроматичности данной спектральной линии. Контур спектральной линии φ(ν) [зависимость интенсивности испускания (поглощения) от частоты] обычно имеет максимум при частоте перехода ν_ki или вблизи неё за Ш. с. л. принимают разность частот, которым соответствует уменьшение интенсивности вдвое (её называют иногда полушириной спектральной линии). Если не учитывать Доплера эффект, Ш. с. л. Δν_ki определяется суммой ширин уровней энергии E_k и E_{i 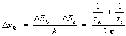 ki} тем больше, чем меньше времена жизни τ_kи τ_i.

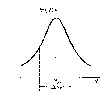
Симметричный контур спектральной линии. Частоте ν_ki соответствует максимальная интенсивность φ(ν) испускания; ∆ν_ki — ширина спектральной линии, равна интервалу между частотами, которые соответствуют интенсивности, вдвое меньшей максимальной.

Вопрос28 Доплеровское расширение спектральной линии.

В опрос 29: Тонкая структура спектров, спин

В атомной физике тонкая структура (мультиплетное расщепление) описывает расщепление спектральных линий атомов, , которое определяется разницей в энергетических уровнях различных атомных орбиталей. Однако при более детальном исследовании каждая линия проявляет свою детальную тонкую структуру. Эта структура объясняется малыми взаимодействиями, которые немного сдвигают и расщепляют энергетические уровни. Их можно анализировать методами теории возмущений. Тонкая структура атома водорода на самом деле представляет собой две независимые поправки к боровским энергиям: одна из-за релятивистского движения электрона, а вторая из-за спин-орбитального взаимодействия.

Спин — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.

Спин измеряется в единицах ħ (приведённой постоянной Планка, или постоянной Дирака) и равен 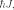  где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).

В связи с этим говорят о целом или полуцелом спине частицы.

Существование спина в системе тождественных взаимодействующих частиц является причиной нового квантовомеханического явления, не имеющего аналогии в классической механике: обменного взаимодействия.