Вопрос 22 Магнитный резонанс (эпр, ямр).

МАГНИТНЫЙ РЕЗОНАНС, резонансное (избирательное) поглощение радиочастотного излучения некоторыми атомными частицами, помещенными в постоянное магнитное поле. Большинство элементарных частиц, подобно волчкам, вращаются вокруг собственной оси. Если частица обладает электрическим зарядом, то при ее вращении возникает магнитное поле, т.е. она ведет себя подобно крошечному магниту. При взаимодействии этого магнитика с внешним магнитным полем происходят явления, позволяющие получить информацию о ядрах, атомах или молекулах, в состав которых входит данная элементарная частица. Метод магнитного резонанса представляет собой универсальный инструмент исследований, применяемый в столь различных областях науки, как биология, химия, геология и физика. Различают магнитные резонансы двух основных видов: электронный парамагнитный резонанс и ядерный магнитный резонанс.

Электронный парамагнитный резонанс (ЭПР). ЭПР был открыт в 1944 русским физиком Е.К.Завойским. Электроны в веществах ведут себя как микроскопические магниты. В разных веществах они переориентируются по-разному, если поместить вещество в постоянное внешнее магнитное поле и воздействовать на него радиочастотным полем. Возврат электронов к исходной ориентации сопровождается радиочастотным сигналом, который несет информацию о свойствах электронов и их окружении. Такой метод, представляющий собой один из видов спектроскопии, применяется при исследовании кристаллической структуры элементов, химии живых клеток, химических связей в веществах и т.д.

Ядерный магнитный резонанс (ЯМР). ЯМР был открыт в 1946 американскими физиками Э.Перселлом и Ф.Блохом. Работая независимо друг от друга, они нашли способ резонансной «настройки» в магнитных полях собственных вращений ядер некоторых атомов, например водорода и одного из изотопов углерода. Когда образец, содержащий такие ядра, помещают в сильное магнитное поле, их ядерные моменты «выстраиваются» подобно железным опилкам вблизи постоянного магнита. Эту общую ориентацию можно нарушить радиочастотным сигналом. По выключении сигнала ядерные моменты возвращаются в исходное состояние, причем быстрота такого восстановления зависит от их энергетического состояния, типа окружающих ядер и ряда других факторов. Переход сопровождается испусканием радиочастотного сигнала. Сигнал подается на компьютер, который обрабатывает его. Таким путем (метод компьютерной ЯМР-томографии) можно получить изображения. (При изменении внешнего магнитного поля малыми ступенями достигается эффект трехмерного изображения.) Метод ЯМР обеспечивает высокую контрастность разных мягких тканей на изображении, что крайне важно для выявления больных клеток на фоне здоровых. ЯМР-томография считается более безопасной, нежели рентгеновская, поскольку не вызывает ни разрушения, ни раздражения тканей. ЯМР позволяет также изучать живые клетки, не нарушая их жизнедеятельности. Поэтому следует ожидать, что применение ЯМР в клинической медицине будет расширяться.

Вопрос 25: Оператор момента импульса и квантовые числа атома водорода. Момент импульса в квантовой механике Оператор момента

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на   (  с чертой), определяемой, как постоянная Планка, поделенная на  . Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновой момент импульса всегда кратен 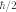  . Например, электрон в состоянии покоя имеет момент импульса  .

Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции: 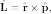где   и   — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

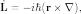
где   — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная,

Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел.

Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.

Параметр n, называемый главным квантовым числом, совпадает с номером уровня энергии и принимает целые положительные значения n=1,2,3,... .

Параметр l называется орбитальным (азимутальным) квантовым числом, характеризующим модуль момента импульса электрона. При данном значении главного квантового числа l может принимать n различных значений (l =0,1,2,…,n–1).

Параметр m называется магнитным квантовым числом и характеризует пространственную ориентацию орбиты электрона. Этот параметр при данном l принимает (2l–1) разных значений: m=–l,–(l–1), ... , 0, ... , (l–1), l. Атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях с одинаковым квантовым числом n, отличающихся значениями квантовых чисел l и m. Состояния электрона с различными значениями l имеют условные обозначения (символы), показанные в таблице 604.1, в которой также приведены возможные значения квантовых чисел l и m при заданном n.

n	1	2		3			4
l	0	0	1	0	1	2	0	1	2	3
m	0	0	-1,0,+1	0	-1,0,+1	-2,-1,0,+1,+2	0	-1,0,+1	-2,-1, 0,+1,+2	-3,-2,-1, 0,+1,+2,+3
символ	1s	2s	2p	3s	3p	3d	4s	4p	4d	4f