Вопрос 1: Классическая теория ачт. Законы Стефана-Больцмана, Вина, Кирхгофа.

Плотность потока энергии, испускаемой излучающим телом во всех направлениях, называют энергетической светимостью тела . Единица измерения   ватт на метр квадратный (1 Вт/ м²).

Введем обозначение для потока энергии, испускаемый единицей поверхности тела в интервале частот d. При малом интервале d поток будет пропорционален d (2.1)

где  спектральная испускательная способность, т. е. плотность потока энергии, испускаемой телом в единичном интервале частот. Энергетическая светимость, или интегральная испускательная способность, связана со спектральной испускательной способностью соотношением

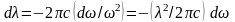, (2.2)

где с – скорость света в вакууме. Тогда (2.3)

Если диапазоны d и d, входящие в выражения (2.1) и (2.3), соответствуют одному и тому же интервалу dR, т. е. 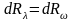, то с учетом (2.2) получаем (2.4)

Соотношение (2.4) устанавливает взаимосвязь между плотностями потока энергии приходящимися на единичные интервалы частоты и длины волны.

Пусть на элементарную площадку поверхности тела падает поток лучистой энергии , обусловленный электромагнитными волнами, частота которых заключена в интервале d. Часть этого потока ( ) будет поглощена телом. Безразмерная величина, определяемая соотношением называется поглощательной способностью тела. По определению, значение не может быть больше 1.

Испускательная ( ) и поглощательная ( ) способности любого тела связаны между собой. Эта связь устанавливается законом Кирхгофа: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является универсальной для всех тел функцией частоты (длины волны) и температуры. Это отношение называют универсальной функцией Кирхгофа

, универсальная функция Кирхгофа есть не что иное, как испускательная способность абсолютно черного тела. Если пользоваться функцией Кирхгофа для длины волны , то связь между функциями следующая: (2.5)

Абсолютно черных тел в природе не существует, однако если в ограниченном диапазоне частот (или длин волн) поглощательная способность тела зависит от  и T так же, как и у АЧТ, то такое тело можно считать абсолютно черным в определенном интервале частот. Например, сажа или платиновая чернь имеют поглощательную способность близкую к единице лишь в ограниченном интервале частот.

М

Рис. 2.1

ожно создать устройство, достаточно близкое по своим свойствам к абсолютно черному телу. Схематическое изображение АЧТ представлено на рис. 2.1. Оно представляет собой почти замкнутую полость с малым отверстием. Излучение, проникшее внутрь через отверстие, прежде чем выйти обратно из отверстия, претерпевает многократные отражения от зачерненной поверхности. При каждом отражении часть энергии поглощается, в результате чего практически все излучение поглощается такой полостью.

Английский ученый Стефан в 1879 г., анализируя экспериментальные данные для различных тел, пришел к выводу, что энергетическая светимость любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов. Так, Больцман в 1884 г., исходя из термодинамических соображений, получил теоретическое выражение для энергетической светимости абсолютно черного тела , (3.1)

где  = 5,7  10^ Вт  (м²К⁴) есть постоянная Стефана – Больцмана; Т – абсолютная температура. Формула (3.1) является математической формулировкой закона Стефана – Больцмана. Таким образом, вывод, к которому пришел Стефан для серых тел, оказался справедливым только для абсолютно черных тел.

Воспользовавшись, кроме термодинамики, электромагнитной теорией, в 1893 г. В. Вин показал, что функция спектрального распределения энергии излучения должна иметь вид

, где F – некоторая функция отношения частоты к температуре. Для функции с учетом (2.5) получается выражение

, (3.2)

где – некоторая функция произведения . Соотношение (3.2) позволяет установить зависимость между длиной волны , на которую приходится максимум функции , и температурой. Продифференцировав соотношение (3.2) по  и приравняв первую производную к нулю, получим

, (3.3)

г

Рис. 3.1

де b = 2.9  10^3 м  К – универсальная постоянная. Формула (3.3) получила название закона Вина, или закона смещения Вина. Экспериментальные зависимости испускательной способности абсолютно черного тела от длины вол­ны показаны на рис. 3.1. Разные кривые соответствуют различным значениям температуры АЧТ. Площадь под каждой кривой численно равна энергетиче­ской светимости АЧТ при соответствующей температуре. Из анализа представленных на рис. 3.1 результатов следует, что энергетическая светимость АЧТ возрастает с увеличением температуры. Максимум испускательной способности, а следовательно, и с увеличением температуры сдвигается в сторону более коротких волн.