§2.10. Относительное равновесие жидкости
ВО ВРАЩАЮЩЕМСЯ СОСУДЕ
Относительным равновесием жидкости называется такой случай ее движения, при котором отдельные ее частицы не смещаются одна относительно другой, и вся масса жидкости движется как твердое тело.
П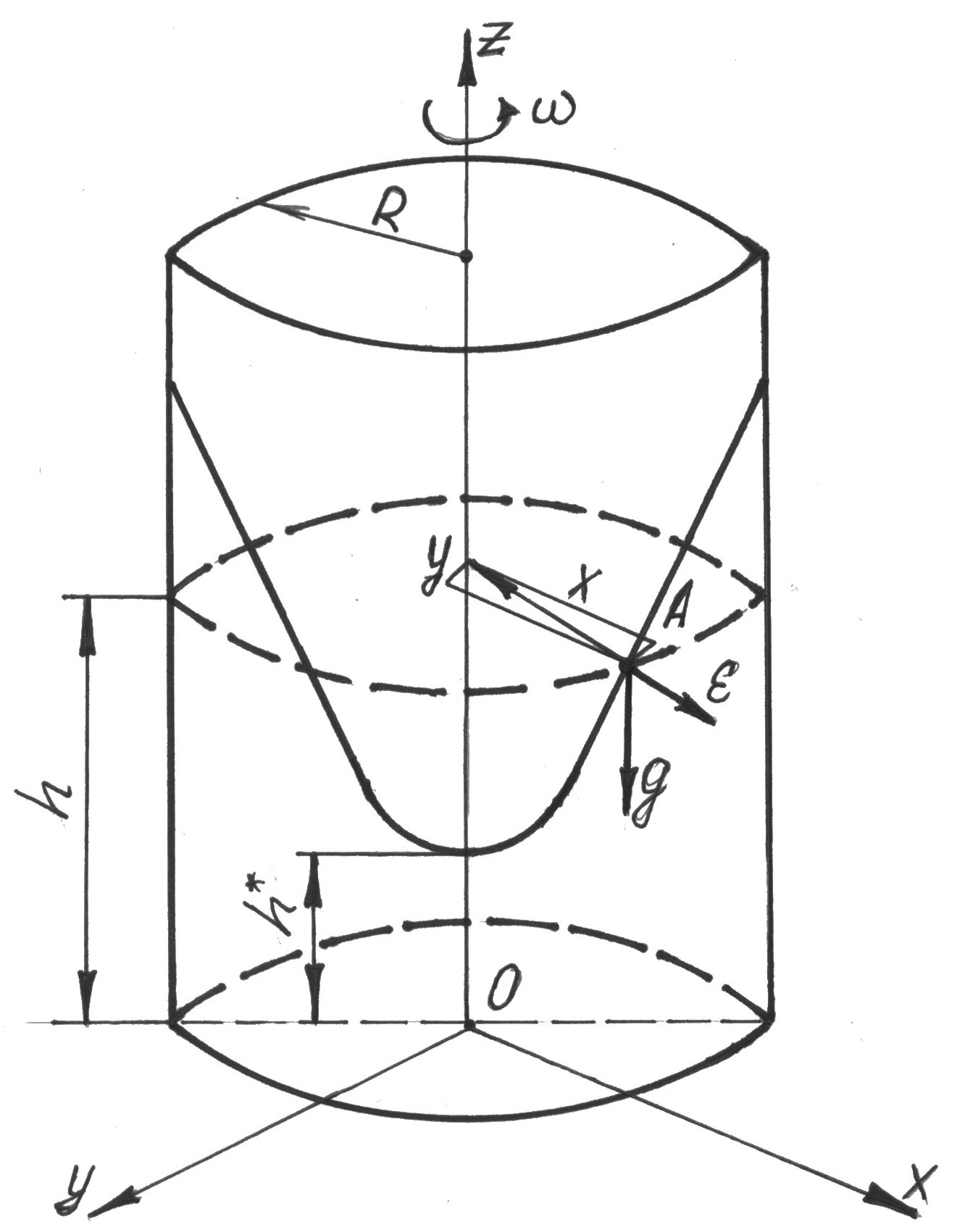
редположим,
что цилиндр, наполненный жидкостью до
высоты h,
приведен во вращательное движение
вокруг вертикальной оси OZ
с угловой скоростью ω
(рис.2.11).
Рис 2.11
Вращающиеся стенки цилиндра приведут во вращение ближайшие к стенкам слои жидкости, а затем, вследствие вязкости жидкости, и всю ее массу. По истечении некоторого времени вся жидкость будет вращаться, примерно стой же угловой скоростью ω, что и сосуд.
Допустим, что такой момент времени наступил. Рассмотрим два интересующих нас вопроса.
1. Какую форму будет иметь поверхность равного давления, и в частности, свободная поверхность?
2. Каков закон распределения гидростатического давления?
Чтобы ответить на поставленные вопросы, рассмотрим уравнение поверхности равного давления (2.31). Для нахождения проекций ускорения выберем в жидкости точку А и покажем ускорения возникающие под действием сил, действующих в жидкости. Силами, действующими в жидкости, являются сила земного тяготения (направленная вертикально вниз по оси OZ) и центробежная сила (направленная вдоль оси ОХ к периферии). В результате действия этих сил полное ускорение точки А будет складываться из ускорения свободного падения g и центробежного ускорения ε.
Составляющие массовых сил, действующих в данном случае на жидкость, X, Y, и Z будут равны:
;
;
, (2.34)
где εх, εy – проекции центробежного ускорения по осям х и y.
Подставляя выражения (2.34) в уравнение (2.31) получаем
. (2.35)
После решения уравнения (2.35) относительно dz и его интегрирования получаем
. (2.36)
Постоянную интегрирования С находим из следующих условий: Х = 0, Y= 0, Z = h*. Следовательно С= h* , т.е. постоянная интегрирования равна глубине залегания самой нижней точки свободной поверхности (вершины параболы).
С учетом постоянной интегрирования С, и при условии, что величина h* определяется из условия неизменности первоначального объема жидкости, т.е.
, (2.37)
уравнение (2.36) принимает вид:
. (2.38)
Полученное уравнение (2.38) является уравнением свободной поверхности жидкости во вращающемся сосуде. Согласно полученному уравнению (2.38), формой свободной поверхности является параболоид вращения.
В уравнении (2.38), x2 + y2= r2, где r – координата рассматриваемой точка А. При условии, что r = R, т.е. рассматриваемая точка А находится на внутренней поверхности вращающегося сосуда, наблюдается максимальный подъем жидкости на высоту zmax. Для определения zmax в уравнение (2.38) подставляем выражение x2 + y2= r2 и получаем
. (2.39)
Согласно полученному уравнению (2.39) можно сделать вывод, что жидкость во вращающемся сосуде поднимается на столько, на сколько и опускается.
Теперь установим закон распределения гидростатического давления.
Подставляя выражения (2.34) в уравнение (2.13) получим
. (2.40)
Выполняя интегрирования уравнения (2.40) получим
. (2.41)
Постоянную интегрирования С находим из следующих условий: Х = 0, Y= 0, Z = h*, р=ратм.
С учетом вышеперечисленного, уравнение (2.41) принимает следующий вид:
(2.42)
или
. (2.43)
Уравнения (2.42) и (2.43) являются уравнениями закона распределения гидростатического давления.