Глава 2

ГИДРОСТАТИКА

§2.1. Силы, действующие в жидкости. Понятие

ОБ ИДЕАЛЬНОЙ ЖИДКОСТИ

Силы, действующие в жидкости, подразделяются на объемные (массовые) и поверхностные. Объемные силы, пропорциональны объему жидкости (к ним относятся силы тяжести и инерции), а поверхностные силы пропорциональны площади поверхности, на которую они действуют (например, сила атмосферного давления на поверхность жидкости в открытом сосуде и сила вязкости).

При выводе основных закономерностей в гидравлике вводится понятие о гипотетической идеальной жидкости, которая в отличие от реальной (вязкой) жидкости, абсолютно несжимаема под действием давления, не изменяет плотности при изменении температуры и не обладает вязкостью. Использование понятия об идеальной жидкости существенно упрощает решение многих задач гидродинамики, а справедливость полученных зависимостей проверяется и устанавливается проведением гидравлических экспериментов. В гидростатике понятие об идеальной и реальной жидкости совпадают.

§2.2. Гидростатическое давление и его

СВОЙСТВА

В предыдущей главе указывалось, что гидростатика изучает условия равновесия жидкостей. Рассмотрим некоторый объем жидкого тела, находящегося в равновесии (рис.2.1).

Р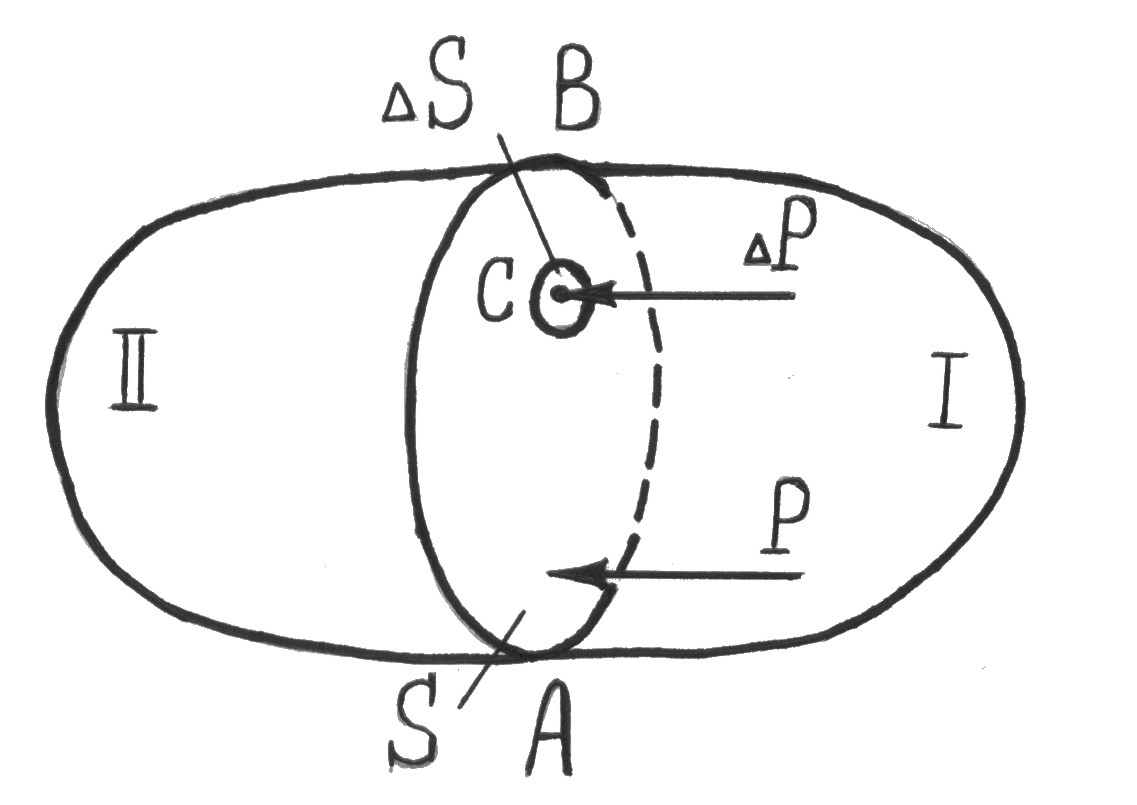 ис 2.1

Разделим плоскостью АВ данный объем на две части. Обозначим площадь плоскости раздела через S, и мысленно отбросим часть 1. Тогда для сохранения оставшейся части 2, заменим воздействие на нее со стороны части 1 силой Р. Эта сила называется силой гидростатического давления на площадку S. Разделив силу гидростатического давления Р на величину площади S, получим среднее гидростатическое давление р_ср. Пусть в плоскости АВ имеется точка С. Выделим возле нее элементарную площадку ΔS. Силу, действующую на эту площадку обозначим через ΔР. Добиваясь, что ΔS → 0, получим предел отношения силы ΔР к площадке ΔS, называемый давлением в точке, которое определяется по формуле

. (2.1)

Свойства гидростатического давления.

1. Гидростатическое давление всегда направлено по внутренней нормали к площадке, на которую оно действует.

Докажем это свойство. Доказательство производим методом от противного. Рассмотрим некоторый объем жидкости в состоянии равновесия (рис.2.2). Разделим объем жидкости произвольно на две части плоскостью CD. На поверхности раздела возьмем точку А и предположим, что сила гидростатического давления в ней направлена не по нормали к площадке, на которой расположена точка А. Тогда силу гидростатического давления можно разложить на две составляющие – на нормальную Р_н и касательную Р_к. Существование касательной составляющей Р_к, приведет к тому, что жидкость выйдет из равновесия, т.е. нарушиться исходная предпосылка о равновесии жидкости. Следовательно, единственно возможным, является нормальное действие гидростатического давления на выбранную площадку.

Д окажем теперь, что гидростатическое давление может быть направлено только по внутренней нормали. Предположим, что оно направлено по внешней нормали в точке В (рис.2.2).

Рис 2.2

В этом случае возникновение растягивающей силы гидростатического давления вызвало бы появление касательных напряжений. Тогда жидкость пришла бы в движение, что опять противоречит условию о равновесии. Следовательно, единственно возможным направлением гидростатического давления является направление по внутренней нормали.

2. Гидростатическое давление в любой точке жидкости не зависит от ориентировки площадки, на которую оно действует, т.е. гидростатическое давление действует одинаково по всем направлениям

Д окажем это свойство. Рассмотрим равновесие некоторого объема жидкости. Для этого примем точку О объема жидкости за начало прямоугольной системы координат и на осях этой системы выделим бесконечно малый тетраэдр Оавс (рис.2.3).

Рис 2.3

Всю жидкость вне тетраэдра отбросим, и будем рассматривать его равновесие. При равновесии тетраэдра сумма проекций по координатным осям действующих на него сил должна быть равна нулю. На тетраэдр, выделенный из жидкости, согласно указанному выше первому свойству гидростатического давления, действуют силы гидростатического давления, направленные нормально к площадкам (граням) тетраэдра внутрь него. Кроме поверхностных сил на тетраэдр действует массовая сила в виде его веса. Чтобы получить уравнения равновесия, необходимо определить составляющие сил давления и собственного веса тетраэдра по координатным осям. Обозначим гидростатическое давление в точке О тетраэдра через р, а его составляющие по координатным осям х, у, z и нормали к площадке авс через р_х, р_у, р_z и p_n. Силы гидростатического давления на грани тетраэдра будут выражаться произведением среднего гидростатического давления на площади этих граней:

; (2.2)

Обозначим собственный вес тетраэдра (силу тяжести) – через G, выразим ее проекции на координатные оси х, у, z и направление n:

(2.3)

где ρ – плотность;

X, Y, Z, N – проекции ускорения массовой силы (силы тяжести) или

проекции единичной массовой силы на оси х, у, z и

направление n.

Сопоставляя выражения сил гидростатического давления (2.2) с выражениями компонентов силы собственного веса (2.3), видим, что проекции сил давления являются бесконечно малыми величинами второго порядка, а проекции массовой силы – третьего порядка. Поэтому при составлении уравнений равновесия сил, действующих на тетраэдр, проекциями массовой силы можно пренебречь ввиду их малости по сравнению с проекциями сил давления. Тогда уравнения равновесия будут иметь следующий вид:

(2.4)

В правой части системы уравнений (2.4) даны конусы углов между направлением гидростатического давления p_n и соответствующими осями х, у, z. Величины проекции площадки авс на соответствующие координатные плоскости, т.е. произведение площади треугольника авс на косинусы соответствующих углов, могут быть представлены площадями соответствующих граней тетраэдра , , . Подставляя эти значения проекций площадок авс в правую часть уравнений (2.4) и деля каждое из уравнений соответственно на , , , получим

(2.5)

Если допустить, что элементарный тетраэдр Оавс уменьшается и в пределе превращается в точку, то из системы уравнений (2.5) может быть получено следующее равенство

. (2.6)

Равенство (2.6) выражает второе свойство гидростатического давления.

3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Это положение не требует специальных доказательств, т.к. ясно, что по мере увеличения погружения точки под уровень давление в ней будет возрастать и, наоборот, по мере уменьшения погружения – уменьшаться. Третье свойство гидростатического давления может быть записано в виде следующего выражения

. (2.7)