§ 3.6 Диаграммы бернулли

Приведем пример использования уравнения Бернулли на примерах потоков идеальной и реальной жидкостей, движущихся через трубопровод.

Выберем два поперечных сечения 1-1 и 2-2 (рис. 3.5). Установим в центрах тяжести сечений 1-1 и 2-2 две вертикальные открытые с обеих сторон трубки.

Прямые трубки называются пьезометрическими; в них жидкость поднимается на высоту, отвечающую гидростатическому давлению в точках погружения , т.е. эти приборы измеряют пьезометрические напоры и .

Рис 3.5

В трубках с нижними концами, направленными навстречу потоку (трубках Пито), уровень жидкости будет выше, чем в пьезометрических, т.к. трубки Пито показывают сумму пьезометрических и скоростных напоров и .

Линия Е-Е проведенная по горизонту жидкости в трубках Пито называется напорной линией (линией гидродинамического напора). Для идеальных жидкостей она всегда горизонтальна. Для реальных жидкостей напорная линия всегда идет по нисходящей.

Линия Р-Р называется пьезометрической линией. Для идеальных и реальных жидкостей пьезометрическая линия может быть горизонтальной или иметь уклон как вверх по направлению движения жидкости, так и вниз (в зависимости от изменения площади живого сечения потока).

Фигура, ограниченная пьезометрической линией и плоскостью сравнения «00», представляет собой эпюру изменения статического напора вдоль потока. Фигура, заключенная между напорной и пьезометрической линиями характеризует изменение скоростного напора вдоль потока.

§ 3.7 Принципы измерения скорости и расхода

ЖИДКОСТИ

У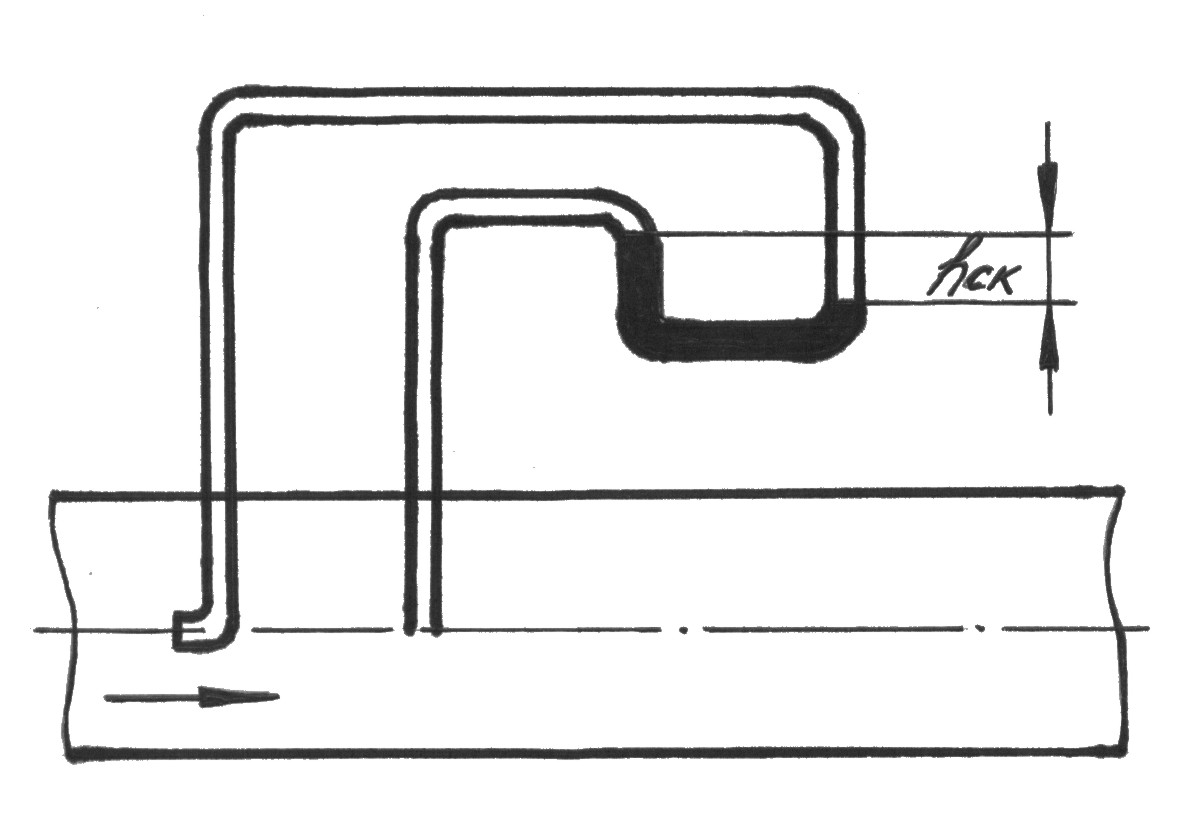 равнение Бернулли широко используется при конструировании и расчете приборов для измерения скорости и расхода жидкостей (пневмометрических трубок и дроссельных приборов). Из рис. 3.6 следует, что для экспериментального определения скорости движения жидкости необходимо знать разность высот поднятия жидкости в трубке Пито и пьезометре, т.е. скоростной напор:

.

Рис 3.6

По найденной таким образом величине h_ск находят скорость в той точке, где установлен наконечник трубки Пито: .

Пьезометры и трубки Пито называются пневмометрическими трубками. Для удобства определения скорости вместо двух вышеуказанных пневмометрических трубок используется одна U-образная, представляющая собой разновидность дифференциального манометра (рис. 3.6). U-образная трубка заполнена жидкостью, которая на смешивается с рабочей и имеет большую плотность, чем последняя. По результатам измерений скоростного напора находим скорость жидкости.

Б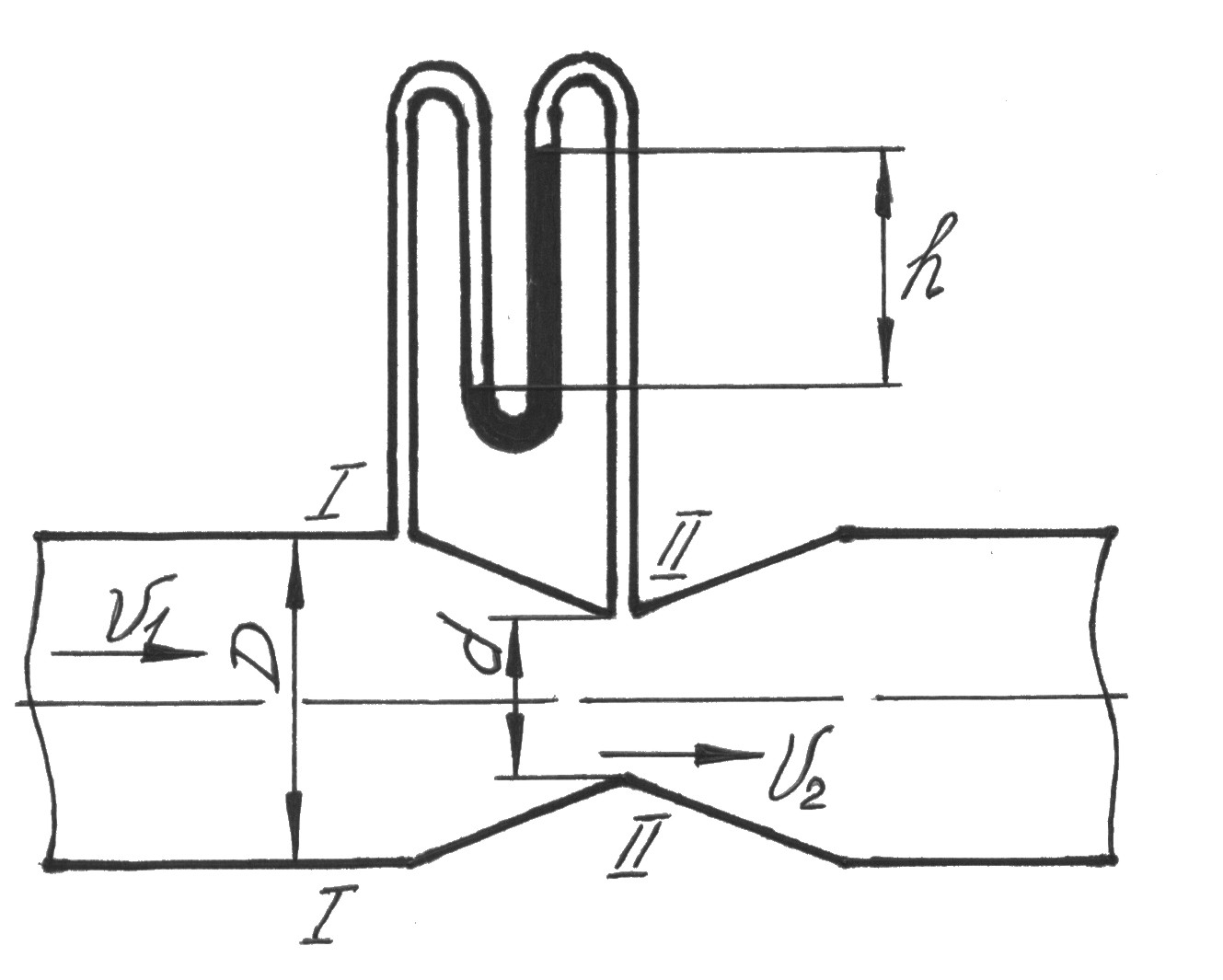 олее широкое распространение , чем пневмометрические трубки, получили дроссельные приборы. Принцип их действия основан на измерении перепада давлений при изменении поперечного сечения трубопровода. В дроссельных приборах создается искусственное сужение потока, следовательно, скорость и кинетическая энергия в более узком сечении возрастают, что приводит к потере (уменьшению) потенциальной энергии (давления) в том же сечении. Поэтому, измерив дифференциальным манометром перепад давлений между сечением трубопровода до его сужения и сечением в самом сужении, можно вычислить напор между сечениями, а по нему – скорость и расход жидкости. В качестве дроссельных приборов используются мерные диафрагмы, сопла и трубы Вентури.

Рассмотрим трубу Вентури (рис. 3.7).

Рис 3.7

Она имеет постепенно сужающееся сечение, которое затем расширяется до первоначального размера. Считая трубопровод горизонтальным, запишем уравнение Бернулли относительно оси трубопровода для сечений 1-1 и 2-2, в которых установлены отборники давления:

.

По закону сплошности потока или . Отсюда . Подставим это выражение в уравнение Бернулли:

.

Отсюда , где h – показание дифференциального манометра. Тогда средняя скорость υ₁ равна

, (3.17)

а расход жидкости будет .

При выводе уравнения (3.17) не были учтены потери энергии при движении жидкости через прибор. Практически их можно учесть , введя коэффициент расхода трубы Вентури μ<1. Тогда получим

. (3.18)

Из уравнения (3.18) видно, что для определения расхода жидкости нужно знать постоянную прибора, зависящую от его размеров:

. (3.19)

Коэффициенты Кориолиса можно принимать равными α₁=α₂=1,1. Коэффициенты для новых труб Вентури составляют μ=0,985, а для бывших в употреблении μ=0,98.

Вопросы для самопроверки

1. Что называется расходом жидкости? Единицы измерения расхода жидкости?

2. Что называется линией тока? Что называется трубкой тока и элементарной струйкой? Какая модель потока называется струйной моделью движения жидкости?

3. Запишите уравнение постоянства расхода?

4. С учетом каких сил выводятся дифференциальные уравнения движения Эйлера?

5. Запишите уравнение Бернулли для элементарной струйки идеальной жидкости? Геометрический и энергетический смысл составляющих уравнения Бернулли?

6. Запишите уравнение Бернулли для потока реальной жидкости? Что представляют собой суммарные гидравлические потери?

7. Что учитывает коэффициент Кориолиса? Какие основные правила выбора сечений?

8. Принцип действия дроссельных приборов? Какова область их применения?