28. Частица в одномерной яме с абсолютно непроицаемыми стенками.

Одномерная прямоугольная «потенциальная яма» с бесконечно высокими «стенками» описывается потенциальной энергией вида

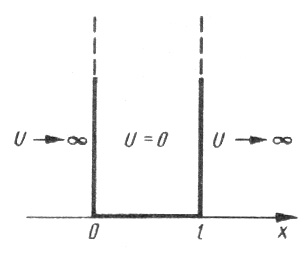
где l – ширина «ямы», а энергия отсчитывается от ее дна (рис. 63).

Пси-функция частицы зависит только от координаты х, поэтому стационарное уравнение Шредингера имеет вид (105)

Частица за пределы «ямы» не проникает, т. е. в областях х<0 и х>1 ψ(х) = 0, а из условия непрерывности следует, что и на границах «ямы» . (106)

В пределах «ямы» (0 ≤ х ≤ l) уравнение Шредингера (105) сведется к уравнению или , (107)

где . (108)

Общее решение уравнения (106): ψ(x)=Asinkx + Bcoskx.

Так как, по (106), , то В=0. Тогда ψ(x)=Asinkx. (109)

Условию ψ(l) = Asinkl = 0 удовлетворяет равенство

k = πп/l (n = 1, 2, 3, ...) (110)

[значение n = 0 приводит к тривиальному результату ψ(х) = 0, а отрицательные значения п – к тем же функциям, но с отрицательным знаком, что не дает новых физических решений].

Из выражений (108) и (110) получим, что собственные значения энергии частицы (n = 1, 2, 3, ...), (111)

т. е. спектр энергии частицы является дискретным (или квантованным). Квантованные значения Е_n называют уровнями энергии, а число п, их определяющее, – квантовым числом.

Собственные функции задачи получаются подстановкой (110) в (109): ,

а коэффициент А находится из условия нормировки

,

откуда . Тогда нормированные собственные функции

(n = 1, 2, 3, ...). (112)

Из формулы (111) следует, что существует минимальная, не равная нулю энергия ,

соответствующая основному состоянию частицы. Волновая функция основного состояния .

Наличие отличной от нуля минимальной энергии противоречит классической механике и не противоречит соотношению неопределенностей. В самом деле, частица «зажата» в области, на границах которой , поэтому ее положение известно с неопределенностью . Тогда, согласно соотношению неопределенностей [см. (74)], неопределенность импульса . Таким образом, энергия никогда не может быть равна нулю, поскольку это потребовало бы выполнения условия . Состояние с энергией Е₁ называют основным состоянием, а остальные состояния – возбужденными. Энергии возбужденных состояний равны 4Е₁, 9Е₁, 16Е₁,..., соответственно значениям квантового числа n = 2, 3, 4, .... .

29. Квантовый гармонический осцилятор.

Квантовый линейный (одномерный) гармонический осциллятор – система, совершающая одномерное движение под действием квазиупругой силы.

Потенциальная энергия линейного гармонического осциллятора

, (113)

где т – масса частицы, ω₀ – собственная частота колебаний осциллятора, х – отклонение от положения равновесия. Зависимость (113) имеет вид параболы (рис. 65), т. е. «потенциальная яма» в данном случае является параболической.

Оператор Гамильтона для осциллятора в квантовой теории имеет вид . (114)

Рис. 65

Записав стационарное уравнение Шредингера в операторной форме [см. (104)] и учитывая (114), придем к уравнению Шредингера для гармонического осциллятора

, (115)

где Е – полная энергия осциллятора.

Опуская подробное решение волнового уравнения (115) приведем полученные собственные функции линейного гармонического осциллятора , (116)

где – полином Чебышева-Эрмита n - го порядка: ;

функции (116) нормированы так, что .

Нормированные волновые функции стационарных состояний квантового осциллятора: (n = 0) (117)

(n = 1) (118)

(n = 2) (119)

Анализируя волновые функции (117) – (119), видим, что функция (117) вообще не обращается в нуль (кроме ), функция (118) обращается в нуль при х = 0. Точка, в которой волновая функция обращается в нуль, называется узлом. Функция (119) обращается в нуль при , т. е. имеет два узла. Таким образом, квантовое число определяет число узлов собственной волновой функции.

(п = 0, 1, 2, ...). (120)

Формула (120) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. квантуется.

. При т. е. энергетические уровни осциллятора совпадают с величинами квантованной энергии осциллятора, постулируемыми Планком в теории излучения черного тела.

Из формулы (120) вытекает важный результат: минимальная энергия квантового осциллятора , т. е. его энергия не может обращаться в нуль (конечно, при ω₀ ≠ 0), в то время как в классической теории энергия основного состояния – состояния покоя – равна нулю. Существование минимальной энергии (энергия нулевых колебаний) является типичной для квантовых систем и представляет собой прямое следствие соотношения неопределенностей.

Плотность вероятности обнаружить частицу на оси х определяется квадратом модуля волновой функции .