
- •Понятие события, классификация
- •Классическое определение вероятности
- •Элементы комбинаторного анализа
- •Действия над событиями.
- •Теорема сложения вероятностей несовместных событий
- •Условная вероятность. Теорема умножения вероятностей. Независимые события.
- •Теорема сложения вер-тей совместных событий
- •Формула полной вероятности. Формула Байеса
- •Повторные независимые испытания. Формула Бернулли
- •Приближенные вычисления вероятностей в схеме испытаний Бернулли
- •Закон распределения случайной величины.
- •14.Математические операции над дсв
- •15.Математическое ожидание дсв
- •16.Дисперсия дсв
- •17.Функция распределения вероятностей случайной величины
- •21.Основные законы распределения дсв
- •Распределение Пуассона
- •Гипергеометрическое распределение
- •18.Теорема о вер-ти отдельно взятого значения нсв
- •20.Числовые характеристики случайных величин
- •22.Равномерный закон распределения нсв
- •23.Нормальная кривая. Влияние параметров на ее форму.
- •24.Свойства случайной величины, распределенной по нормальному закону.
17.Функция распределения вероятностей случайной величины
Описание
распределения
набором вероятностей
![]() не
очень удобно: слишком много существует
борелевских множеств. Мы описали
дискретные
распределения
таблицей распределения, абсолютно
непрерывные —
плотностью распределения. Попробуем
поискать какой-нибудь универсальный
способ описать любое возможное
распределение.
не
очень удобно: слишком много существует
борелевских множеств. Мы описали
дискретные
распределения
таблицей распределения, абсолютно
непрерывные —
плотностью распределения. Попробуем
поискать какой-нибудь универсальный
способ описать любое возможное
распределение.
Можно
поставить вопрос иначе: распределение
есть набор вероятностей попадания в
любые борелевские
множества
на прямой. Нельзя ли обойтись знанием
вероятностей попадания в какой-нибудь
меньший набор множеств на прямой?
Борелевская
![]() -алгебра
-алгебра
![]() порождается
интервалами
(равно как и лучами
порождается
интервалами
(равно как и лучами
![]() ),
поэтому можно ограничиться только
вероятностями попадания в такие лучи
для всех
),
поэтому можно ограничиться только
вероятностями попадания в такие лучи
для всех
![]() .
А уже с их помощью можно будет определить
и вероятность попасть в любое борелевское
множество.
.
А уже с их помощью можно будет определить
и вероятность попасть в любое борелевское
множество.
Замечание.
Можно
с таким же успехом ограничиться набором
вероятностей попадания в интервалы
![]() ,
или в
,
или в
![]() ,
или в
,
или в
![]() .
.
Определение.
Функцией
распределения
случайной величины
![]() называется
функция
называется
функция
![]() ,
при каждом
равная
вероятности случайной величине
принимать
значения, меньшие
,
при каждом
равная
вероятности случайной величине
принимать
значения, меньшие ![]() :
:
![]()
Перечислим основные дискретные и абсолютно непрерывные распределения и найдём их функции распределения.
Если функция распределения F (x) непрерывна, то случайная величина называется непрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p (x), которая связана с функцией распределения F (x) формулами
 и
и
![]() .
.
Отсюда,
в частности, следует, что для любой
случайной величины
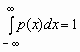 .
.
21.Основные законы распределения дсв
Биномиальным называют закон распределения Д.С.В. Х - числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна р, вер-ть возможного значения Х=k (числа k появлений события) вычисляют по формуле Бернулли: Pn (k)=Cn^k* p^k *q^(n-k)
Распределение Пуассона
Говорят,
что случайная величина
![]() имеет
распределение
Пуассона
с параметром
имеет
распределение
Пуассона
с параметром
![]() ,
где
,
где
![]() ,
и пишут:
,
и пишут:
![]() ,
если
принимает
значения
,
если
принимает
значения
![]() с
вероятностями
с
вероятностями
![]() .
Таблицу распределения
читатель
может нарисовать самостоятельно.
.
Таблицу распределения
читатель
может нарисовать самостоятельно.
Гипергеометрическое распределение
Говорят,
что случайная величина
имеет
гипергеометрическое
распределение
с параметрами
![]() ,
,
![]() и
и ![]() ,
где
,
где
![]() ,
,
![]() ,
если
принимает
целые значения
,
если
принимает
целые значения
![]() такие,
что
такие,
что
![]() ,
,
![]() ,
с
вероятностями
,
с
вероятностями
![]() .
Случайная величина с таким распределением
имеет смысл числа
белых шаров
среди
шаров,
выбранных наудачу и без возвращения
из урны, содержащей
белых
шаров и
.
Случайная величина с таким распределением
имеет смысл числа
белых шаров
среди
шаров,
выбранных наудачу и без возвращения
из урны, содержащей
белых
шаров и
![]() не
белых.
не
белых.
18.Теорема о вер-ти отдельно взятого значения нсв
Вероятность попадания НСВ в заданный интервал
Вер.
попадания СВ Х в задан. интервал
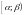 равна приращению ее функции распредел.
на этом интервале, т.е. вер. того, что
(
равна приращению ее функции распредел.
на этом интервале, т.е. вер. того, что
(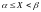 )=
F(
)=
F( )
- F(
)
- F( ).
Эта формула следует из формулы F(
).
Эта формула следует из формулы F(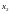 )=F(
)=F(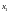 )+
P(
)+
P( )
– вопрос №24, если вместо точек
)
– вопрос №24, если вместо точек
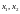 взять точки
и
.
Вер. любого отдельного значения
непрерывн. СВ равна 0. Доказ-во:
Воспользуемся равенством (
взять точки
и
.
Вер. любого отдельного значения
непрерывн. СВ равна 0. Доказ-во:
Воспользуемся равенством (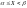 )=
F(
)=
F( )
- F(
)
- F( )
и устемим
)
и устемим
 к
к
 (
( ).
Тогда получим
).
Тогда получим
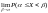 =
=
 .
В левой части последн. рав-ва в пределе
вместо вер. попадания значения СВ в
интервал
.
В левой части последн. рав-ва в пределе
вместо вер. попадания значения СВ в
интервал
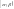 получим вер. того, что СВ приняла отдельно
взятое значение
получим вер. того, что СВ приняла отдельно
взятое значение
 ,
т.е.
,
т.е.
 .
Значение предела в правой части рав-ва
зависит от того, явл. ли функц. F(x)
непрерывн. в точке
или имеет в ней разрыв. Если функц. имеет
разрыв, то предел равен величине скачка
функции F(x) в точке
.
Значение предела в правой части рав-ва
зависит от того, явл. ли функц. F(x)
непрерывн. в точке
или имеет в ней разрыв. Если функц. имеет
разрыв, то предел равен величине скачка
функции F(x) в точке
 .
Т.к. по предположению функц. F(x) всюду
непрерывна, то
.
Т.к. по предположению функц. F(x) всюду
непрерывна, то
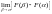 = F(
)
- F(
= F(
)
- F( )
= 0. Т.о.
)
= 0. Т.о.
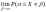 =
=
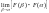 =
=
 =0.
При непрерывн. распределении вероятностей,
т.е. когда функц. распредел. непрерывна,
вер. попадания значения непрерывн. СВ
на сколь угодно малый участок отлична
от 0, тогда как вер. попадания в строго
определен. точку равна 0. Воспользовавшись
последн. св-вом, докажем, что для
непрерывн. СВ выполняются след. рав-ва:
Р(
=0.
При непрерывн. распределении вероятностей,
т.е. когда функц. распредел. непрерывна,
вер. попадания значения непрерывн. СВ
на сколь угодно малый участок отлична
от 0, тогда как вер. попадания в строго
определен. точку равна 0. Воспользовавшись
последн. св-вом, докажем, что для
непрерывн. СВ выполняются след. рав-ва:
Р( )
=
)
=
 =
=
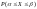 =
=
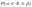 .
Докажем одно из соотношений. Соб.
.
Докажем одно из соотношений. Соб.
 представл. собой сумму 2-ух несовместн.
событий
представл. собой сумму 2-ух несовместн.
событий
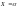 и
и
 .
Тогда по теореме сложения вер. имеем
Р(
.
Тогда по теореме сложения вер. имеем
Р(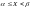 )
=
)
=
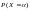 +
+
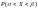 .
Согласно последн. св-ву
.
Согласно последн. св-ву
 =0,
тогда
=0,
тогда
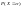 +
=
+
=
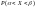 = F(
= F( )
- F(
)
- F( ).
Следоват-но
).
Следоват-но
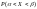 =
F(
)
- F(
=
F(
)
- F( )
)
19.. Плотность вероятности НСВ
Функц.
распредел. вероятностей непрерывной
СВ дает полную вероятностн. хар-ку ее
поведения. Однако задание непрерывн.
СВ с пом. функц. распредел. не является
единственным. Ее можно задать с пом.
др. функции, кот. назыв. дифференциальн.
функц. распределения или плотностью
распредел. вероятностей. Пусть X
– несрерывн. СВ с интервальн. функц.
распредел. F(x).
F(x)
непрерывна и дифференцируема в
исследуемом интервале. Рассмотрим вер.
попадания значения СВ в интервал (x;
x+ x).
P(x<X<x+
x)
= F(x+
x)
– F(x),
т.е. вер. равна приращению функц. на этом
участке. Определим вер., кот. приходится
на единицу длины рассматриваемого
участка. Для этого разделим обе части
последн. рав-ва на
x:
x).
P(x<X<x+
x)
= F(x+
x)
– F(x),
т.е. вер. равна приращению функц. на этом
участке. Определим вер., кот. приходится
на единицу длины рассматриваемого
участка. Для этого разделим обе части
последн. рав-ва на
x:
 =
=
 =
=
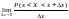 =
=
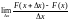 =
=
 .
=
f(x).
Опред.:
Дифференц. функц. распредел. или
плотностью распредел. вер. называется
1-ая производная от интегральн. функции
распредел. Замеч.: Для хар-ки распредел.
вер. дискретн. СВ дифференц. функция
распредел. непременима.
.
=
f(x).
Опред.:
Дифференц. функц. распредел. или
плотностью распредел. вер. называется
1-ая производная от интегральн. функции
распредел. Замеч.: Для хар-ки распредел.
вер. дискретн. СВ дифференц. функция
распредел. непременима.
