4. Действия над событиями.

Д иаграмма Вьенна-Эйлера

А) событие A

Б) Сложение – событие, кот состоит в том, что происходит хотя бы одно из событий A или B

В) произведение событий- А и B одновременно

Г) Дополнение – событие принадлежит к А, но не принадлежит к B

Д) противоположное событию A событие В

Е) Несовместимые события – если они не могут произойти одноременно

Ж) События образуют полную группу, если хотя бы одно из них обязательно происходит в результате испытания

З) А влечет за собой В

5. Теорема сложения вероятностей несовместных событий

Пусть события А и В несовместны, причем вероятности этих событий известны. Теорема: Вероятн. появления одного из 2-ух несовместн. событий(безразлично какого) равна сумме вероятностей этих событий, т.е. P(A+B) = P(A)+P(B). Доказ-во: Пусть n – возможн. элементарн. исходов испытания. m₁ – число исходов благоприятствующ. событию А; m₂ – число исходов благоприятств. событию В. Тогда P(A)=m₁/n; P(B)=m₂/n. Т.к события А и В несовместны, то нет таких исходов, кот. благоприятствовали бы одновремен. и событию А, и соб. В. Поэтому событию А+В благоприятствует m₁+m₂ элементарн. исходов испытания. Тогда P(A+B)=(m₁+m₂)/n=m₁/n+m₂/n=P(A)+P(B). Следствие: Вероятн. появления одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий, т.е. P(A₁+A₂+…+A_n)=P(A₁)+P(A₂)+…+P(A_n) или P(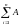 _i)=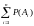

Теорема: Сумма вероятностей событий А₁, А₂…А_n, образующих полную группу равна 1, т.е. P(A₁)+P(A₂)+…+P(A_n)=1. Доказат-во: Т.к. появление одного из событий полной группы достоверно, а вероятн. достоверн. события равна 1, то P(A₁+A₂+…+A_n)=1. Любые 2 события полной группы несовместны, поэтому можно применить теорему сложения: P(A₁+A₂+…+A_n)= P(A₁)+P(A₂)+…+P(A_n)

Теорема:Сумма вероятн. противоположн. событий равна 1, т.е. P(A)+P(Ā)=1. Доказат-во: Противоположн. события образуют полную группу, а сумма вероятностей событий, образующих полную группу равна 1. Замечание: Если вероятн. одного из противоположн. событий обозначить за p, а вероятн. другого через q, то предыдущ. формулу можно записать в виде: p+q=1.

6. Условная вероятность. Теорема умножения вероятностей. Независимые события.

Событие А называется независимым от события В, если вероятн. события А не зависит от того, произошло событие В или нет. Событие А называется зависим. от события В, если вероятн. соб. А меняется в зависим. от того, произошло соб. В или нет. Определ.: Вер. Соб. А, вычисленная при условии, что имело место др. соб. В, называется условной вероятностью события и обозначается P_В(A) или P(A\B). Условие независимости соб. А от соб. В можно записать в виде P_В(A)=P(A). Условие зависимости соб.: P_B(A)≠P(A). Теорема: Вероятн. произведения 2-ух событий равна произв. вероятн. одного из них на условн. вероятн. другого, вычисленную при условии, что 1-ая имела место, т.е. P(AB)=P(A) P_A(B). Доказат-во: Пусть возможн. исходы опыта сводятся к n случаям. Предположим, что событию А благоприятств. m случаев, а соб. В – k случаев. Т.к. мы не предполагали соб. А и В несовместными, то существуют случаи благоприятн. и соб. А, и соб. В одновременно. Пусть число таких случаев 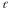, тогда вероятн. соб. АВ будет равна /n, а P(A)=m/n. Вычислим условн. вероятн. соб. В в предположении, что соб. А имело место. Если известно, что соб. А произошло, то из ранее возможных n случаев остаются возможными только те m случаев, кот. благоприятствовали соб. А, а из них только случаев благоприятствуют соб. В, поэтому P_A(B)= /m. Подставляя в выражения вероятн. события АВ, вер. событ. А и условн. вероятн. соб. В, получаем тождество.

Замечание: При применении теоремы безразлично, какое из соб. А и В считать 1-ым, а какое 2-ым, т.е. P(AB)= P(A) P_A(B)= P(B) P_B(A)