1.Понятие дифференциального уравнения, его порядка и решения. Пусть W - область в пространстве Rⁿ⁺² и функция F(x,y,U₁,…,U_n) определена на W . Опр 1. Обыкновенным дифференциальным уравнением ­­порядка n называется выражение вида: F(x,y,y^I,…,y⁽ⁿ⁾)=0 (1), где x - независимая переменная, y(x)-функция от x, y^I(x),...,y⁽ⁿ⁾(x) -производная от y(x), n-порядок. Опр 2. Функция y=j(x) определенная на промежутке I=<a,b> называется решением дифференциального уравнения (1), если выполняются условия : 1) j(x)ÎCⁿ(I); 2)"xÎI: точка с координатами (x, j(x), j^I(x)…j⁽ⁿ⁾(x))ÎW; 3) "xÎI: F(x,j(x),j^I(x),…,j⁽ⁿ⁾(x))=0 Пусть D-область, D<Rⁿ⁺¹ _{X ,Y ,U1 , …, Un-1} В D определена функция f(x,y,u₁,…,u_n-1). Если F(x,y,u₁,…,u_n)= u_n -F(x,y,u₁,…,u_n-1), где F(x,y,u₁,…,u_n-1) определена в DÌ Rⁿ⁺¹, то уравнение f(x,y,y¹,…,y^(n-1))= y⁽ⁿ⁾ называется разрешенным относительно старшей производной. ------------------------------------------------------------------------------------------------------------------------------------------------------------

2. ОДУ первого порядка, разрешенные относительно производной. Понятия решения и интегральной кривой уравнения. Постановка задачи Коши. Пусть область D в пространстве R² и f(x,y) определена на D. y’=f(x,y) (1) - ОДУ 1-го порядка разрешенная относительно производной. Опр 1. Функция y=j(x) определена на промежутке I=<a,b> называется решением уравнения (1) если выполняются условия: 1) j(x)ÎC¹(I); 2) "xÎI:(x,j(x))ÎD; 3)"xÎI: j'(x)=f(x,j(x)). Опр 2. Если y=j(x)- решение (1), то график этой функции называется интегральной кривой уравнения (1). Постановка задачи Коши.(постановка задачи- необходимость понять, что известно и что нужно найти)ДАНО: Область DÌR², f(x,y)-определена в D и точка (x₀,y₀)ÎD (или числа (x₀,y₀)ÎD). НАЙТИ: решения y=j(x) уравнения (1) определенное на I, такое что j(x₀)=y₀ (т.е. интегральная кривая проходящая через (x₀,y₀)), числа (x₀,y₀) называются начальными условиями. Условная запись задачи Коши.Найти решение y’=f(x,y) удовлетворяющее условию y(x₀)=y₀. Замечания:1)Если функция f(x,y) непрерывна в D то для "(x₀,y₀)ÎD задача Коши имеет решение в любой точке D.2)Если f(x,y) непрерывна в D то (1) имеет бесконечно много решений.3) (x₀,y₀)ÎD. Для единственности требуется единственное условие. --------------------------------------------------------------------------------------------------------------------------------------------------------3. Формулировка теоремы существования и единственности ( ТСЕ ). Понятие общего решения. Пусть f(x,y) определена обл. DÌR² , точка (x₀,y₀)ÎD. Рассмотрим задачу Коши (1)(y’=f(x,y)(2);y(x₀)=y₀). Пусть j₁(x) и j₂(x) решения решение задачи Коши (1), т.е. j₁(x),j₂(x)-решение урав-я(2) и j₁(x₀)=y₀, j₂(x₀)=y₀. Опр 1. Говорят, что задача Коши(1) имеет единст решение если любые два реш. j₁(x) и j₂(x) этой задачи совпадают на некот. окр-сти точки x₀ $d>0 "xÎ(x₀-d,x₀+d):j₁(x)ºj₂(x) ТСЕ(Локальная):Пусть на обл. DÌR² функ.f(x,y) и ее част. производная (¶x/¶y)(x,y) опред-ы и непрерывны, и точка (x₀,y₀) ÎD. Тогда урав. y’=f(x,y) имеет решение j(x): 1)опред. на некот. окр-сти (x₀-h,x₀+h) точки x₀, удовл. условию j(x₀)=y₀; 2)такое решение единственно. Замечание к ТСЕ. Пусть в обл D выполн. усл. ТСЕ. 1)В D бесконечно много решений уравнений, x₀-точка(x₀,y₀)ÎD.Через эту точку проходит реш. y=j(x,y₀).Все эти решения не совпадают. 2)Решение задачи Коши(1) может быть опред-но лишь на некот окр-сти x₀. Опр 2.Пусть f(x,y) удовл в D условиям ТСЕ. Функцию y=j(x,c) наз-ют общим решения урав(2) в обл D, если: 1)"c:j(x,c)-реш(2); 2)" частное решение урав(2) может быть получено из j(x,c) подбором соотве-его значения c. --------------------------------------------------------------------------------------------------------------------------------------------------------4. Уравнения с разделяющимися переменными. Однородные уравнения.Примеры. Уравнение вида(1) y’=f(x)*g(y) наз.урав-ем с разделяющимися переменными. Теорема 1. Пусть функция f(x)-непрерывна на интервале (a,b), а функция g(y)-непрерывна на (c,d), причем для "yÎ(c,d): g(y)¹0. Тогда через любую точку прямоугольника D={(x,y),a<x<b,c<y<d} проходит единственное решение урав-я (1).Однородное уравнение.Уравнения вида(2) y^I=f(y/x) называется однородным, где x-неиз.переменная u=y/x, y^I=u^Ix+u; Уравнение(2) преоб-ем к виду: f(u)=u^Ix+u, u^I=f(u)-u/x

5.Линейные уравнения первого порядка. Уравнения Бернулли. Ур-е вида(1) y^/+p(x)y=f(x)-наз.линейным урав-ем 1-ого порядка. Теор 1. Пусть функция р(х) и f(x) непрерывны на интервале α<x<β. Тогда через любую точку(х₀;у₀) полосы D={(х;у); α<x<β, -∞<y<+∞}проходит единственное решение ур-я (1) причем оно определено на (α;β). Уравнение(1) однородное, если f(x)≡0 и неоднородно в противном случае. Уравнение Бернулли.Уравнение вида(2)y’+p(x)y=f(x)yⁿ называется урав-м Бернулли(n≠0,1).Если n>0, то y≡0 –реш.урав-я(2).Разделим урав-е (2) на yⁿ: y’/yⁿ +p(x)*1/y^n-1=f(x).Введем новую завис-ю перем-ю: z(x)=1/y^n-1,z’(x)=(y^n-1)’=(1-n)y^-ny’=(1-n)*y’/yⁿ; z’+(1-x)p(x)z=(1-n)f(x)-линейное относительно z(x). --------------------------------------------------------------------------------------------------------------------------------------------------------6. Обобщенное понятие интегральной кривой. Понятие интеграла и общего интеграла ОДУ первого порядка. Уравнение в полных дифференциалах. Пусть область D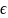 R² . Опр 1. Пусть P(x,y) и Q(x,y) непрерывны в обл.D. Кривая γ ={(x,y), x=φ(t), y=ψ(t), t I=< α, β>} называется интегральной кривой ур-я (1)P(x,y)dx+ Q(x,y)dy=0,если выполняются условия: 1) φ(t), ψ(t) С¹(I); 2) 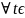I: (φ(t), ψ(t)) D ;3) I: P((φ(t), ψ(t)) φ ⁽¹⁾(x)+Q((φ(t), ψ(t)) ψ⁽¹⁾(t)≡0 Опр 2. Если интегральная кривая ур-я (1) задаётся в виде Ф(х,у)=0, то это ур-е будем называть интегралом ур-я (1). Опр 3. Уравнение F(х,у)=С называется общим интегралом ур-я (1), если 1) : F(х,у)=С – интеграл ур-я (1) ;2) Любой интеграл ур-я можно получить подбором соответствующих произвольны[ постоянных С. Уравнение в полных дифференциалах: Пусть P(x,y) и Q(x,y) С¹(D), ур-е (2)P(x,y)dx+ Q(x,y)dy=0 называется ур-ем в полных дифференциалах ,если существует U(x,y) С¹(D) такая, что dU(x,y)= P(x,y)dx+ Q(x,y)dy, (2) dU(x,y)= P(x,y)dx+ Q(x,y)dy=0, ясно что dU(x,y)= 0 U(x,y)=С. Теорема 1. Пусть D-односвязная область R²_x,y ,функции P(x,y) и Q(x,y) непрерывно диффер-ы на D, тогда урав-е(2) является уравн-м в полных диффер-х, если: (x,y) D: ¶P(x,y)/¶y=¶Q(x,y)/¶x --------------------------------------------------------------------------------------------------------------------------------------------------------7.ОДУ порядка n: определение решения, постановка задачи Коши, формулировка ТСЕ. Пусть Ω область в прост-ве Rⁿ⁺¹ и в Ω задана непрер-я фун-я f(x,y,u₁,…u_n-1). Соотношение вида(1) y⁽ⁿ⁾ = f( x, y, y’, ... , y^{(n – 1)} ) называется ОДУ порядка n, разрешенным относительно старшей производной. Опр 1. Фун-я φ(x) определенная на промежутке I=<α;β>, наз. реш-ем ур-я (1), если выполняются условия: 1) φ(x) Є С_n(I); 2) x Є I точка : (x ,φ(x), φ’(x) ,…, φ^(n-1)(x)) Є Ω; 3) x Є I точка : φ⁽ⁿ⁾(x) ≡ f(x, φ(x), φ’(x), …, φ^(n-1)(x)). Постановка задачи Коши. Пусть Ω обл пр-ва Rⁿ⁺¹ _, f(x,y,u₁,…u_n-1). определена и непрер в Ω , числа x₀, y₀ , y₀’,…, y₀ ^(n-1) такие, что (x₀, y₀ , y₀’,…, y₀ ^(n-1) ) Є Ω. НАЙТИфун-ю , определенную на интервале (x₀-δ; x₀+δ) являющуюся реш-ем урав-я (1) и удовлетворяет условиям y₀ = φ(x₀), y₀’=φ’(x₀),…, y₀ ^(n-1) = φ^(n-1)(x₀),где (x₀, y₀ , y₀’,…, y₀ ^(n-1) )-начальные условия .Запись задачи Коши: y⁽ⁿ⁾ = f(x,y,y’,... ,y ^{(n – 1)} ) , y(x₀) = y₀ , y’(x₀) = y₀’ , … , y^(n-1)(x₀) = y₀ ^(n-1). ТСЕ(локальная):Пусть Ω-область в Rⁿ⁺¹ ; x₀, y₀ , y₀’,…, y₀ ^(n-1) ) ,числа, такие, что (x₀, y₀ , y₀’,…, y₀ ^(n-1) ) Є Ω. Если фун-я f(x,y,u₁,…u_n-1) и ее част. призв ∂f /∂u_i (x,y,u₁,…u_n-1)(i=1,…,n-1) непрерывны в обл. Ω, то в некоторой окрестности (x₀-h; x₀+h) существует решения урав-я y⁽ⁿ⁾ = f( x, y, y’, ... , y^{(n – 1)} ), удовлетворяющее условиям: y(x₀) = y₀ , y’(x₀) = y₀’ , … , y^(n-1)(x₀) = y₀ ^(n-1) и это решение единственно. --------------------------------------------------------------------------------------------------------------------------------------------------------8.Лин-е диффир-е урав-е (ЛДУ) порядка n. Формулировка ТСЕ и задачи Коши для ЛДУ высшего порядка. Пусть a₀(x), a₁(x), … , a_n(x), f(x) определены на I=<α,β>.Уравнение вида (1) a₀(x)*y⁽ⁿ⁾ + a₁(x)*y^(n-1) + … +a_n-1(x)*y’ + a_n(x)*y = f(x) называется ЛДУ порядка n (a₀(x) ≠ 0).Если a₀(x) ≠ I на I, то обозначим:P_i(x) = a_i(x)/a₀(x); i=1,…,n; f(x) = b(x)/a₀(x);(2) y⁽ⁿ⁾ + p₁(x)*y^(n-1) + … + p_n-1(x)*y’ + p_n(x)*y = f(x) (неоднородное ЛДУ порядка n),если для всех xЄ I выполняется f(x)≡0 ,то(3) y⁽ⁿ⁾ + p₁(x)*y^(n-1) +…+p_n-1(x)*y’ + p_n(x)*y = 0.( однородное ЛДУ порядка n) Постановка задачи Коши.Пусть x₀ Є I, y₀ , y₀’,…, y₀ ^(n-1) - произвольные действ.числа. Найти решение урав-я (1), удовлетворяющее начальным условиям: y(x₀) = y₀ , y’(x₀) = y₀’ , … , y^(n-1)(x₀)= y₀ ^(n-1). ТСЕ(ЛДУ порядка n).Пусть функции p₁(x) , … , p_n(x) , f(x) непрерывны на промежутке I=<α,β> , точка х₀ Є I, y₀ ,y₀’ , … , y₀ ^(n-1) - произвольные действ. числа .Тогда существует единственное решение уравнения (2), удовлетворяющее начальному условию: y(x₀) = y₀ , y’(x₀) = y₀’ , … , y^(n-1)(x₀) = y₀ ^(n-1), определённое на всём промежутке I=<α,β>.Замечание к ТСЕ 3.Пусть x₀ Є I, ур. (3) – однородное, и начальные условия:y(x₀) = 0 , y’(x₀) = 0 , … , y^(n-1)(x₀) = 0. Эта задача Коши имеет только нулевое решение y ≡0.

9.Лду порядка n и линейный дифференциальный оператор. Свойства решений однородного лду.

Пусть p₁(x)…p_n(x) непрерывна на промежутке I=<a;b>

Рассмотрим оператор L, L: c⁽ⁿ⁾(I)->c(I)

L=dⁿ/dxⁿ +p₁(x)d^n-1)/dx^n-1+...+p_n-1(x)d/dx+p_n(x) d⁰/dx⁰; d⁰/dx⁰(f)=f⁽⁰⁾ = f; ;

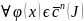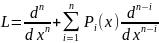Теор 1.Пусть p₁(х)…p_n(х) c(I)

1) Если y₁(х) и y₂(х) –реш-я ЛДУ порядка n,и α₁,α₂-произвольные числа,то α₁y₁+α₂y₂-решение ЛДУ порядка n.

2)Если комплексная функция F(x)=U(x)+iV(x). Действительная часть ReF(x)=U(x) и JmF(x) = iV(x) – решение уравнения ЛДУ порядка n

--------------------------------------------------------------------------------------------------------------------------------------------

10.Линейно зависимые и линейно независимые системы функций. Определитель Вронского и необходимое условие линейной зависимости произвольной системы функций.

1)Пусть ф-ции 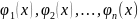называются лин. зависимыми на I, если найдутся числа 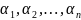не все равные нулю, такие, что на I выполняется тождество:

х

2)Функ. называются лин. независимыми на I, если выполняется тожд-во: )

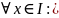Определитель вида:

W(x)=W{y₁(x),y₂(x)…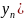 )}= 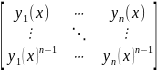называется определителем Вронского функций y₁(x),y₂(x)… ) на промежутке I.

Теор 1. Пусть y₁(x),y₂(x)… y_n(x) ∈C^(n-1)(I) . Если y₁(x),… y_n(x) линейно зависимы на промежутке I, то х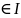 :W(x)

Теор 2. Если y₁(x),… y_n(x) линейно независимы на промежутке I, то х :W(x)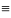 W{ y₁(x),… y_n(x)} ≠0 --------------------------------------------------------------------------------------------------------------------------------------------

11.Теорема об определителе Вронского системы линейно независимых решений однородного лду порядка n.

Теор 1. Пусть решения y1(x),y2(x)…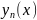 – лин незав на I=(a,b), причем все они являются решениями одного ОЛДУ.

Если y₁(x),y₂(x)…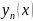 - лин независимы на I, то

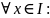
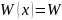[y₁(x),y₂(x)… ]

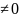
Следствие: Если существует х₀, такое, что W()=0, то y1(x),y2(x)… - линейно зависимы на I. --------------------------------------------------------------------------------------------------------------------------------------------------------

12.Теорема о размерности пространства решений однородного ЛДУ порядка n. Фундаментальная система решений(ФСР) и общее решение однородного ЛДУ порядка n. Рассмотрим (1) L[y]=y⁽ⁿ⁾+ p₁(x) y^(n-1) +….+ p_n-1(x) y’+p_n(x)y=0; p₁(x)...p_n(x) C(I) множество решений урав-я (1) образует линейное подпространство в Сⁿ(I). Теор 1.Пусть p₁(x),…, p_n(x) ∈C(I),тогда пространство решений однородного ЛДУ (1)порядка n конечномерно , и его размерность равна n. Опр 1. Любые n линейно независимых решений однородного ЛДУ порядка n называются ФСР этого уравнения. Опр 2. Пусть 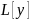=f(x)- ЛДУ порядка n. Общим решением ЛДУ порядка n на некотором промежутке I называют функцию y=F(x,C₁,C₂,…,C_n), определенную на I, где (C₁,C₂,…,C_n –произвольные постоянные числа), из которой любое решение урав-я получается подбором соответ-х значений произвольных постоянных C^/₁ ,C₂^/,…,C_n^/.