Формула при отсутствии внешних сил

Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.

, где

 — масса ракеты

 — её ускорение

• — скорость истечения газов

 — расход массы топлива в единицу времени

17. Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы.

Момент силы относительно точки

Если имеется материальная точка  , к которой приложена сила  , то момент силы относительно точки   равен векторному произведению радиус-вектора  , соединяющего точки   и  , на вектор силы  : .

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Моментом пары называется взятое со знаком "плюс" или "минус" произведение модуля сил, образующих пару, на ее плечо. Момент пары сил по­ложителен, если пара стремится вращать тело против часовой стрелки, и отрицателен в противоположном случае.  

18. Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.

Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен:   .

 Момент инерции всего тела относительно оси равен:  

 для непрерывно распределенной массы:   .

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: ,

19. Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.

21. Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется т.е. не изменяется с течением времени.

22. Плоское движение.Плоскопаралле́льное движе́ние (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости.Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге.

23. Работа и энергия. Работа на элементарном и конечном пути. Мощность, средняя мощность.

Работа - физическая величина, равная произведению силы, перемещения и косинуса угла между направлением действия силы и перемещением: А = Fs cos a.

Энергия — универсальная мера различных форм движения и взаимодействия.

Элементарная работа

Работа на конечном пути \Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы

Мощность

P=F v cosa

Ср.Мощность

мгновенная мощность

24.

Работа силы тяжести вблизи поверхности Земли. Работа силы упругости. Работа сил трения и работа по преодолению трения. Консервативные и диссипативные силы.

Работа силы тяжести вблизи поверхности Земли

Работа силы упругости. A_упр = - (k*x₂²/2 - k*x₁²/2)  

Работа сил трения A_mp = −F_mpS

работа по преодолению трения W=Fs=μF_норм s

Консервативные и диссипативные силы.

Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:

К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными(диссипативными) силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

25.

Механическая энергия. Кинетическая энергия. Зависимость изменения кинетической энергии от работы внешних сил.

В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. 

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек.

Зависимость изменения кинетической энергии от работы внешних сил.

26.

Потенциальная энергия. Поле. тяготения вблизи поверхности Земли, потенциальная энергия упругой деформации. Потенциальная энергия   — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

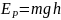
потенциальная энергия упругой деформации

27.

Потенциальная энергия. Поле. тяготения вблизи поверхности Земли, потенциальная энергия упругой деформации.

Потенциальная энергия   — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

потенциальная энергия упругой деформации

28.

Закон сохранения энергии в механике.

29.

Абсолютно неупругий удар. Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются друг с другом и движутся дальше как одно тело.

30.

Абсолютно неупругий удар. Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются друг с другом и движутся дальше как одно тело.

32.

Линейный осциллятор. Циклическая частота, частота, период колебаний, их вычисление для маятников.

Линейный гармонический осциллятор — система, совершающая движение под действием ква­иупругой силы.

Циклическая частота — скалярная физическая величина, мера частоты вращательного или колебательного движения.

Чaстота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени.  Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание

33.

Уравнение свободных гармонических колебаний. Амплитуда, фаза, начальная фаза колебаний. Скорость и ускорение осциллятора, их максимальные значения. Векторная диаграмма, уравнение колебаний в комплексном виде.

Уравнение свободных гармонических колебаний.

Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. 

Фа́за колеба́ний — аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс.

-начальна фаза

Скорость и ускорение осциллятора

v= A cos(t + )

a= -A² sin(t + )

Векторная диаграмма, уравнение колебаний в комплексном виде.

34.

Нахождение с помощью начальных условий амплитуды и начальной фазы колебаний.

35.

Энергия линейного осциллятора, потенциальная яма и потенциальный барьер. Устойчивое равновесие. Применение ЗСЭ для вывода ДУ колебаний.

Потенциа́льная я́ма – область пространства, где присутствует локальный минимум потенциальной энергии частицы.

Потенциа́льный барье́р — область пространства, разделяющая две другие области с различными или одинаковыми потенциальными энергиями.

Устойчивое равновесие — равновесие, при котором малое возмущение системы приводит к её малому отклонению от состояния равновесия. Равновесие тела устойчиво, если:

если его потенциальная энергия имеет минимальное значение;

если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями.

37.

Биения. Сложение взаимно перпендикулярных колебаний. Частные случаи. Бие́ния — явление, возникающее при наложении двух гармонических колебаний, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. 

Сложение взаимно перпендикулярных колебаний

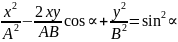
Частные случаи.

 = m(m=0, ±1, ±2, ...)

2)  = (2m+1) (m=0, ± 1, ±2,...).

38.

Осциллятор с затуханием. Сила сопротивления. ДУ колебаний, его решение. Собственная частота, коэффициент затухания. Амплитуда, циклическая частота, частота, период затухающих колебаний. Апериодическое затухание

Осциллятор с затуханием

1) )

2) (γ= )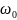

3) ( )

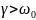Сила сопротивления - это сила (например вес), которую должна преодолеть действующая сила (например, при использовании рычага).

ДУ колебаний, его решение

x=0

Собственная частота

коэффициент затухания

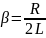
амплитуда затухающих колебаний

циклическая частота

период затухающих колебаний

Апериодическое затухание

39.

Скорость и энергия осциллятора с трением. Время релаксации, логарифмический декремент, добротность

Время релаксации

логарифмический декремент

Добротность

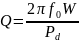
40.

Скорость и энергия осциллятора с трением. Время релаксации, логарифмический декремент, добротность

Время релаксации

логарифмический декремент

Добротность

42.

Волна. Волны продольные и поперечные, гармонические, плоские, механические. Фронт волны. Плоская бегущая монохроматическая волна, её длина, фазовая скорость, волновое число и волновой вектор, частота и циклическая частота. Волновое уравнение.

Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве.

Поперечная волна - волна, в которой частицы среды перемещаются перпендикулярно направлению распространения волны.

Продольная волна - волна, в которой движение частиц среды происходит вдоль направления распространения волны.

Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе.

ПЛОСКАЯ ВОЛНА - волна, у к-рой направление распространения одинаково во всех точках пространства. 

Волново́й фронт — это поверхность, до которой дошли колебания к данному моменту времени.

Плоская монохроматическая бегущая электромагнитная волна -- это электромагнитная волна, в которой E- и H- компоненты поля меняются по одному и тому же гармоническому закону, а поверхность постоянной фазы является плоскостью.

Волновое уравнение

70.

2) Известно, что без смазки, уменьшающей трение, работа сил трения приводит к такому нагреванию, что плавятся подшипники (например, у коленчатого вала автомобиля). В современных быстрорежущих сверлильных и токарных станках нагрев сверл и резцов настолько велик, что для их охлаждения применяют специальные жидкости. С помощью трения сухих кусочков дерева можно добыть огонь, т. е. нагреть дерево до температуры, превышающей температуру его воспламенения. Это умело использовали первобытные люди. Перечисленные выше и подобные им многочисленные опыты показали, что количество теплоты сохраняется только при теплообмене, когда не совершается работа. Количество теплоты не является неуничтожимой и несотворимой жидкостью, оно представляет собой величину, родственную работе. Одинаковое повышение температуры тела может быть вызвано как передачей некоторого количества теплоты Q, так и совершением определенной работы А. Но работа в механике равна изменению энергии системы. Поэтому количество теплоты, как и работу, надо считать мерой изменения энергии системы, и выражать ее в тех же единицах, что и работу, т. е. в джоулях.

3) Предмет термодинамики Предметом рассмотрения классической термодинамики служат связи термодинамических параметров друг с другом и с физическими переменными, вводимыми в рассмотрение в других разделах физики (масса, давление, поверхностное натяжение, сила тока и т. д.). Химические и фазовые реакции (фазовые переходы первого рода) также есть предмет изучения классической термодинамики, поскольку в этом случае рассматриваются связи между массами компонентов системы и их химическими потенциалами

4) 1 закон термодинамики

Первый закон термодинамики или закон сохранения энергии для тепловых процессов, связывает количество теплоты, переданное системе, изменение ее внутренней энергии и работу, совершенную системой над окружающими телами. Одна из возможных его формулировок звучит следующим образом: Количество теплоты, сообщаемое термодинамической системе, равно сумме изменения ее внутренней энергии ΔU и работы A, совершаемой системой против внешних сил. Q = ΔU + A. Если работа совершается внешними силами над термодинамической системой, то, обозначив ее A', первый закон термодинамики можно записать в виде уравнения: Q + A' = ΔU.

Функции состояния и функции процесса. ФУНКЦИЯ СОСТОЯНИЯ       

в термодинамике, функция независимых параметров, определяющих равновесное состояние термодинамич. системы. Ф. с. не зависит от пути (хар-ра процесса), следуя к-рому система пришла в рассматриваемое равновесное состояние (т. е. не зависит от предыстории системы). К Ф. с. относятся, в частности, характеристические функции системы (внутр. энергия, энтальпия, энтропия и др.). Работа и кол-во теплоты не явл. Ф. с., т. к. их значение определяется видом процесса, в результате к-рого система изменила своё состояние.

Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние.

Функции процесса в термодинамике включают:

• количество теплоты и

• термодинамическую работу.

• Эти величины, однако, могут быть «превращены» в функции состояния с помощью интегрирующего множителя:

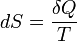• , где 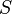  (энтропия) — функция состояния.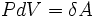

• , где 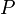  (давление) и 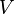  (объём) — функции состояния.

72.

1) Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплотыδQ, полученного телом, к соответствующему приращению его температуры δT:

Единица измерения теплоёмкости в системе СИ — Дж/К.

Молярная теплоёмкость — это теплоёмкость одного моля вещества. Часто употребляется обозначение  .

Связь с удельной теплоёмкостью:

,

где c — удельная теплоёмкость, μ — молярная масса.

Размерность молярной теплоёмкости [Дж/(К•моль)]

Уде́льная теплоёмкость - физическая величина, численно равная количеству теплоты, которое необходимо передать телу массой 1 кг для того, чтобы его температура изменилась на 1 Кельвин. Удельная теплоемкость обозначается буквой c и измеряется в Дж/кг*Кельвин.

Единицей СИ для удельной теплоёмкости является джоуль на килограмм-кельвин. Следовательно, удельную теплоёмкость можно рассматривать как теплоёмкость единицы массывещества. На значение удельной теплоёмкости влияет температура вещества. К примеру, измерение удельной теплоёмкости воды даст разные результаты при 20 °C и 60 °C.

Формула расчёта удельной теплоёмкости:  , где   — удельная теплоёмкость,   — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),   — масса нагреваемого (охлаждающегося) вещества,   — разность конечной и начальной температур вещества.

2)Теплоемкость в различных процессах Теплоемкость газа в изохорическом процессе.

Если газ нагревать или охлаждать в ограниченном объеме, то вся поступающая

теплота идет на изменение температуры газа. Процесс, при котором объем не

меняется, называется изохорическим.

Т.к. объем газа в изохорическом процессе не меняется, то газ не совершает ра-

боты. Поэтому первое начало для изохорического процесса записывается так:

dQ = dU .

Молярная теплоемкость в этом случае равна

С(v)=dQ/dT=dU/dT

индекс означает, что это теплоемкость газа в процессе с неизменным объемом.

Внутренняя энергия одного моля одноатомного газа равна U =3/2 N kT

Ее изменение с температурой будет dU = 3/2N kdT

Подставляя это в выражение для теплоемкости, получаем:

C(v)=3/2N(a)k=3/2R

Мы получили, что любой одноатомный газ при постоянном объеме имеет одну

и ту же теплоемкость, равную 3 /2 R = 12 5, Дж ×моль^(-1) × К^(-1)

Это хорошо согласуется с экспериментом.

Для двухатомного газа при нормальных условиях соответственно c

v = 5/2R

Интересно, что измеряя теплоемкость двухатомного газа мы можем косвенно измерить количество степеней свободы молекул газа. При очень

низких температурах в газе существует только

поступательное движение молекул, в нормаль-

ных условиях молекулы газа участвуют также

во вращательном движении; при высоких температурах в газе “просыпаются”

колебательные степени свободы. Почему количество степеней свободы зависит

от температуры объясняет квантовая механика и мы это пропустим из-за недос-

татка времени.

Теплоемкость газа в изобарическом процессе

Если при нагревании газ остается при постоянном давлении,

то такой процесс называется изобарическим. Это можно на-

пример реализовать с помощью системы, показанной на

рис. 23. В этом случае первое начало термодинамики выгля-

дит так:

dQ = dU + PdV .

Внутренняя энергия dU зависит только от температуры газа

и не зависит от процесса, в котором участвует газ. Поэтому

мы можем здесь использовать выражение, полученное в

предыдущем параграфе: dU = c (v)dT

Нам необходимо привести теперь выражение для работы PdV через dT – в

этом случае бесконечно-малые величины сократятся и мы получим разумное

выражение для теплоемкости. Воспользуемся уравнением Менделеева-

Клапейрона для одного моля:

PV = RT .

Т.к. давление не меняется, то объем пропорционален температуре и

PdV = RdT .

Подставляя это выражение в уравнение первого начала, получим

dQ = c (v)dT + RdT ,

откуда

c (p)=dQ/dT (P=const)= c (v) + R

Мы получили не только теоретическое выражение для теплоемкости газа в изо-

барическом процессе, но и очень важную связь ее с теплоемкостью газа в изо-

хорическом процессе:

c(p)=c(v)+R

Это выражение справедливо для любых газов и хорошо согласуется с экспери-

ментом.

3)Уравнение Маера

Для любого идеального газа справедливо соотношение Майера:

,

где   — универсальная газовая постоянная,   — молярная теплоёмкость при постоянном давлении,   — молярная теплоёмкость при постоянном объёме.

Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарному процессу в идеальном газе:

,

в рассматриваемом случае:

.

Очевидно, уравнение Майера показывает, что различие теплоёмкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной   — механический эквивалент теплоты.