2. Свойства движения.
Будем говорить, что т. B
лежит между точками А и С, и записывать:
10. Движение сохранит отношение лежать между АВС и движение
,
свойство утверждает А’B’C’
Доказательство: из того, что (1)
«f – движение»
(2)
(1), (2)
Следствие: из доказанного свойства следует, что любое движение переводит луч в прямую, отрезок в отрезок, полуплоскость в полуплоскость, угол в угол.
Доказательство: из того, что все перечисленные фигуры определяются при помощи отношения между:
Каждая прямая плоскости разбивает все точки плоскости, не лежащие на этой прямой на 2 класса, также, что для любых 2х точек, принадлежащих одному классу на прямой l не существует, точки, лежащие между ними, для любых 2х точек их различных классов на l существуют точки, лежащие между ними.
Так определ. Классы называются полуплоскостями (открытыми)
Обозначаются: L+ и L-
Пусть дан
где
F1 – полуплоскость, определяющая прямою АВ, содержащую [BC)
F2 – полуплоскость, определяющая прямой ВС, содержащей [BA)
F1, F2 – внутренняя область угла
20. Движение переводит пару параллельных прямых в пару параллельных прямых.
Доказательство:
Доказываем от противного:
Но a || и противоречие
При доказательстве свойства 20, мы не использовали, что f - движение, а использовали только свойство, что движение переводит прямую в прямую. Поэтому свойство 20 – частный случай более общего утверждения.
Лемма: любое преобразование плоскости, переводящее прямую в прямую, сохраняет перпендикулярность прямых.
30. любое движение сохраняет простое отношение 3х точек.
Пусть А, В, С – 3 точки одной прямой
(А, В, С) =
движение:
Доказательство: т.к. А, В, С лежат на одной прямой, а движение переводит прямую в прямую, то их образы А’, B’, C’, принадлежат одной прямой.
Докажем, что движение сохраняет модуль
простого отношения. Обозначим, через
’ отношение
между точками
Но так как, движение сохраняет отношение
между точками, а простое отношение 3х
точек равно нулю, то точки А, В, С, то
движение сохраняет и знак простого
отношения;
40. движение сохраняет величину угла.
Доказательство: пусть дан
тогда
На сторонах угла
зафиксированы т. А.С
Тогда
(1)
Следствие: 1). Движение сохраняет перпендикулярность прямых.
2). Переводит ортонормированный репер в ортонормированный.
Лемма: преобразование плоскости,
которое репер R
переводит в R’
и сохраняет простое отношение 3х
точек, в каждой т.
ставит
в соответствие т.
Доказательство:
Для доказательства достаточно доказать, что координаты точки, выражаются через простое отношение 3х точек.
- произвольная точка
Т.к. f- сохраняет простое
отношение 3х точек, то
3. Аналитическое выражение движения.
Пусть f – движение, тогда ортонормический репер прейдет в ортонормический репер.
Согласно линии 2
Обозначим:
O’(x0,y0)R
L – угол между i,j
E - коэффициент ориентации.
Воспользуемся формулами перехода от R и R’
(1)
Подставим в (1) старые и новые координаты точки M’, получим:
(2)
– задают аналитическое выражение движения.
(3)
(4)
Если f – движение, то коэффициенты в формулах (2) удовлетворяют равенствам (3) и (4). Верно и обратное: если в формулах (2) координаты при неизвестных удовлетворяют равенствам (3) и (4), то f – движение, т.к. в этом случае репер R’- ортонормирован.
Df: если движение не меняет ориентации плоскости, т.е. в формулах (2) Е = 1, то движение называется движением I рода; если меняет ориентацию, т.е. Е = -1, то движение называется движением II рода.
The1: Любое движение однозначно определяется 3 параметрами соответственных точек, не лежащих на одной прямой.
из того, что формулы (2) содержат 5
коэффициентов:
,
а каждая пара соответствующих точек
дает 2 уравнения с этими коэффициентами.
The2: Если род движения известен (т.е .известно Е), то движение определяется 2 парами соответственных точек.
Лекция 23
Классификация движений.
Формулы
показывают, что существуют 2 рода
движений: движение I
рода (Е = 1)
движение II рода (Е = -1)
Прежде, чем рассматривать дальнейшую классификацию движения, рассмотрим некоторые частные случаи.
Параллельный перенос.
Пусть дан а. Параллельный перенос
обозначают: Па:
(1)
Найдем аналитическое выражение параллельного переноса. Выберем
(1)
Па:
Найдем род этого движения
параллельный перенос есть движение I
рода
Поворот вокруг точки О на угол .
Пусть на плоскости задана т. О и - ориентированный угол.
Df: поворотом вокруг т. О
на угол называется
преобразование, которое каждой т.М
ставит в соответствие точку M’,
что
О – центр.
Найдем аналитическое выражение поворота.
Пусть
,
О – центр поворота.
Пусть
Спроектируем т. М и M’ на оси x,y
Из
(1)
Из
(2)
(3)
– аналитическое выражение поворота вокруг начала координат
Найдем род этого движения:
- движение 1го рода
Отражение от прямой (осевая симметрия).
Пусть дана прямая l
Df: Отражением от прямой
е обозначается Ge
и называется преобразование, которое
каждой т. М ставит в соответствие такую
т. М’, что выполняются 2 условия: 1)
2)
середина [MM’]
Выведем на плоскости
,
что
(совпадает)
Пусть
Из того, что
(1)
С – середина
(2)
(1), (2)
Выясним род этого движения
-
движение 2го рода.
Скользящее отражение.
Пусть дана прямая l и a || l
Df: Скользящее отражение
называется произведение отражения
прямой l на параллельный
перенос и обозначается:
Пусть
(1)
Па
(2)
(1)(2), получим формулы, задающие скользящие отражение:
Выясним род этого движения:
-
движение 2го рода
Th1: (теорема Шария)
Любое движение 1го рода является либо параллельным переносом, либо поворотом, при этом, тождественное преобразование плоскости можно рассматривать как перенос на нулевой вектор, или поворот на нулевой угол.
Доказательство:
Пусть f – движение 1го рода
(*)
Рассмотрим возможные расположения точек А, В, С
1.
а).
(1)
(2)
(1), (2)
Тогда Па=АВ:
(*)
Согласно Th наше движение 1го рода будет параллельным переносом.
б).
(*)
,
(3)
(1)
(1), (3)
середина
отрезка АВ. Тогда
(*)
Т.к. поворот движения 1го рода, т.е. соотношение (*), то наше движение совпадает с поворотом.
2.
.Обозначим через
ось
симметрии отрезка АВ (это серединный
перпендикуляр); через
- ось симметрии отрезка ВС.
Т.к.
Рассмотрим поворот вокруг т. О
на угол
(*)
из соотношения (*)
Th: ( теорема Шарля)
Любое движение 2го рода есть либо отражение от прямой, либо скользящее отражение.
Доказательство:
Пусть f – движение 2го рода
(*)
---------------------------------
(1)
Рассмотрим возможные расположения т А, В, С
1).
а). (2)
(1), (2) (3)
Рассмотрим симметрию относительно :
Рассмотрим параллельный перенос на а = АВ
(**)
т.к. движения, род которого известен,
определяется 2 парами соответственных
точек, то из (*), (**)
б). (4)
(1), (4)
Пусть О – середина отрезка АВ
- ось симметрии [ AB ]
(***)
из (*), (***)
В этом случае Th верна
2).
(1)
-
равнобедренный
средняя линия
Рассмотрим симметрию
относительно
Рассмотрим
(5)
С учетом теорем Шарля и формул, аналитически определяющих движение, можно построить следующую таблицу, классифицирующую движение плоскости.
Движение плоскости
Движение 1-го рода
Движение 2-го рода
Параллельный
перенос
Поворот
Отражение от
прямой
Скользящее
отражение
Тождественные
преобразования
Лекция 24
Группы движений плоскости и ее подгруппы.
Th1: Множеству движений плоскости образует группу.
1). Пусть
движ.
(1)
Пусть
движ.
(2)
Тогда преобразование движений
движение
2).
(3)
Рассмотрим обратное произведение:
движение
Из доказанных свойств 1 и 2 множество движений является подгруппой всех преобразований плоскости множество движений есть группа.
Th2: Множество всех точек движений 1го рода образует группу, которая является подгруппой группы движений.
Доказательство:
Каждое движение 1го рода сохраняет ориентацию плоскости, поэтому произведение движений 1го рода и движения обратного движения 1го рода, сохраняет ориентацию плоскости, т.е. является движением 1го рода.
Th3: Множество параллельных переносов образует группу, которая является подгруппой группы движений 1го рода.
Доказательство:
Пусть даны 2 параллельных переноса:
Рассмотрим произведения параллельных
переносов:
.
Значит f является
параллельным переносом на вектор, равный
сумме векторов a и b,
т.е.
Пусть
Следовательно, преобразование обратного переноса есть параллельный перенос
- теорема доказана
Выберем на плоскости прямую
и обозначим через а вектор, параллельный
Рассмотрим множество всех векторов, параллельных фиксированных прямой . Параллельные переносы, определенные этими векторами, назовем параллельными переносами вдоль прямой .
Th4: Множество параллельных переносов вдоль фиксированной прямой образует группу, которая является подгруппой группы всех параллельных прямых.
Доказательство:
Пусть даны 2 пары параллельных переноса
вдоль прямой
:
и
рассмотрим их произведение
но
Пусть дан
Рассмотрим обратное преобразование
Параллельный перенос, обратный параллельному переносу вдоль l есть перенос того же вида.
Th5: Множество поворотов плоскости группы не образует, так как произведение 2х поворотов с различными центрами может быть и не поворотом, а параллельным переносом.
Но множество всех поворотов с
фиксированным центром образует группу,
которая является подгруппой группы
движений 1го рода, т.к.
Если тождественное преобразование рассматривать как параллельный перенос на нулевой вектор или на нулевой угол как поворот, то образует группу, которая является подгруппой параллельного переноса. Доказанные Th позволяют построить таблицу строения группы движений.
Группа движений
Группа движений
1-го рода
Группа параллельных
переносов
Группа поворотов
с фиксированным центром
Группа параллельных
переносов вдоль фиксированной прямой
Группа тождественных
преобразований
Замечание: Множество движений 2го рода группы не образует, т.к. произведение 2х движений 2го рода есть движение 1го рода.
Лекция 23
Подобные образования плоскости.
Определение и свойства.
Пусть дано действительное число k>0
Df: Подобием коэффициента
k (обозначается Пk)
называется преобразование плоскости,
при котором каждой паре точек А, В
ставится в соответствие А’, B’,
что
Из Df любое подобие с коэффициентом k=1 есть движение. Движение есть подобие с k=1.
10.
20. Подобие сохраняет отношение лежать между.
Пусть A, B,
C – 3 точки, такие, что В
лежит между А и С
(1), пусть
, тогда
(2)
Умножим обе части равенства (1) на k:
лежит между A’ и C’
Следствие: любое подобие переводит луч в луч, отрезок в отрезок, прямую в прямую, полуплоскость в полуплоскость, угол в угол.
из того, что все перечисленные фигуры определяются через отношение лежать между.
30. Любое подобие сохраняет параллельность прямых.
из леммы 1, которая утверждает, что: любое преобразование плоскости, переводящее прямую в прямую сохраняет параллельность.
40. Подобие сохраняет величину угла.
Зафиксируем на сторонах угла
АВС, т.
и
(1)
Следствие: подобие сохраняет перпендикулярность прямых.
50.Подобие сохраняет простое отношение 3х точек.
Нужно доказать, что
.
Т.к. подобие сохраняет отношение лежать
между, то оно сохраняет знак простого
отношения 3х точек:
(1).
Рассмотрим модуль
(2)
(1),(2)
60. Любое подобие переводит окружность в окружность.
Дана
Имеет место следующее утверждение: любое преобразование плоскости, переводящее прямую в прямую, и окружность в окружность, является подобием.
Движение является частным случаем подобия. Другим частным видом подобия является гомотетия.
Пусть на плоскости зафиксирована т. S и k 0
Df: Геометрией с центром
в т. S и коэффициентом
называется преобразование плоскости,
при котором каждой точке М ставятся в
соответствие, такая точка M’,
что
Th: Гомотетия с коэффициентом
k является подобие
с коэффициентом |k|;
т.е.
(*)
- подобие с коэффициентом |k|
Из доказанной Th следует, что так как гомотетия – частный вид подобия, то она обладает всеми свойствами подобия, кроме того гомотетия обладает следующими свойствами:
10. каждую прямую переводит в параллельную ей прямую.
20. гомотетия сохраняет ориентацию плоскости.
Аналитическое выражение подобия.
Th: Любое подобие модно представить в виде произведения гомотетии на движение, причем цент можно выбрать произвольно.
Доказательство:
(1)
S
(2)
(1), (2)
(3)
(3)
Выберем на плоскости ДПСК
.
Пусть
На основании предыдущей Th,
Пk можно представить
в виде произведения
(1)
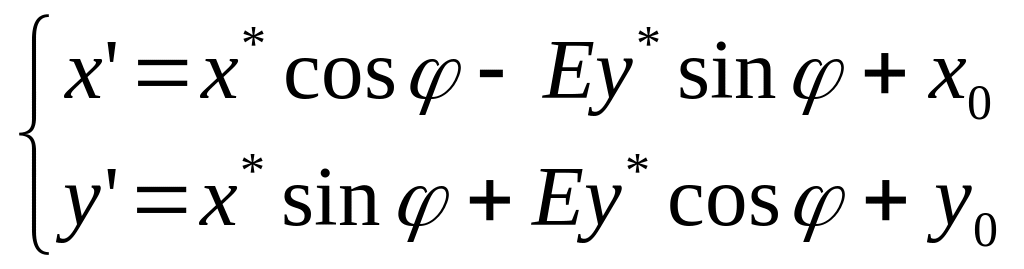(2)
(1)(2)
Если E = 1, то подобие – подобия 1го рода.
Докажем, что гомотетия является подобием
1го рода:
гомотетия
подобия 1го рода.
Группа подобных преобразований.
Th: Множество всех подобных преобразований образует группу, которая является подгруппой группы всех преобразований плоскости.
Доказательство:
1).
(1)
(2)
2). Пусть
Th: Множество подобий 1го рода образует группу.
из того, что 2 подобия сохраняет ориентацию плоскости, то их произведение сохраняет ориентацию плоскости; если подобие сохраняет ориентацию, то и образное подобие сохраняет ориентацию. Следовательно, подгруппой является группа движений и группа движений 1го рода замыкается последняя группа на группу тождественных преобразований. Множество гомотетий не образует группу, т.к. произведение 2х гомотетий с различными центрами может не быть гомотетией. Но множества гомотетий с фиксированным центром образует группу. Последняя группа замыкается на тождественных преобразованиях.
Группа подобий
Группа движений
Группа подобий
1-го рода
Группа движений
1-го рода
Группа гомотетий
с фиксированным центром
Группа тождественных
преобразований
Лекция 24
Группа аффинных преобразований плоскости.
Определение. Аналитическое выражение, свойства.
Пусть на плоскости заданны 2 аффинных репера:
и
Df: Преобразование плоскости,
при котором
называют аффинным преобразованием
плоскости.
Из Df , что если аффинное преобразование f задано парой реперов R и R’, то R’ является образом репера R в этом преобразовании.
Следствие: пусть на плоскости
заданы 2 треугольника:
и
