Системы управления химико-технологическими процессами.

Основные понятия.

Параметры технологического процесса — это физические величины определяющие ход процесса к примеру температура, давление.

Регулируемая величина или регулируемый параметр — это параметр который необходимо поддерживать постоянным или изменять по определённому закону.

Мнгновенное значение — это значение регулируемой величины в данный момент времени.

Измеренное значение — это значение регулируемой величины полученное в рассматриваемый момент времени на основании данных некоторого измерительного прибора.

Объект управления или объект регулирования — это устройство требуемый режим работы которого должен поддерживаться из вне специально организованными управляющими воздействиями.

Управление — это формирование и реализация управляющих воздействий, которые поддерживают нужный режим работы объекта управления.

Регулирование — это частный вид управления, когда задачей является обеспечение постоянства какой либо выходной величины.

Автоматическое управление — это управление без непосредственного участия человека.

Входное воздействие — это воздействие подаваемое на вход системы или устройства оно возникает из цели управления и формируется вне системы, обозначается х.

Выходное воздействие — это воздействие выдаваемое на выходе системы или устройства, обозначается у.

Состояние объекта может измениться в результате двух видов воздействий это управляющие и возмущающие воздействия.

Управляющие воздействия — это воздействие вырабатываемое на исполнительном устройстве, которое непосредственно воздействует на объект управления.

Возмущающее воздействие или внешнее воздействие — это воздействие внешней среды на систему.

Возмущающие воздействия делятся на контролируемые(их можно измерить) к примеру изменение температуры теплоносителя, не контролируемые(их нельзя или нецелесообразно измерять) к примеру активность катализатора, допускающие стабилизацию к примеру потоки в аппарат), не допускающие стабилизацию к примеру температура окружающей среды, внешние к примеру та же температура окружащей среды и внутренние к примеру неравномерность навала вещества или неравномерность плотности вещества.

Схема ручного регулирования.

К примеру есть сушильный шкаф, в нём нужно поддерживать определённую температуру.

Оператор измеряя температуру по ртутному термометру по необходимости замыкает или размыкает рубильник.

х = tзад

схема автоматического регулрования с использованием реле.

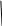
Схема с автоматическим регулированием с электронным мостом.

Электронный мост это схема из нескольких к примеру восьми сопротивлений имеющую две диагонали, имеющая две ветви питающую, на которую подаётся напряжение, и измерительную, с которой снимается измеренное напряжение.

Основное свойство моста это способность находиться в одном из двух состояний уравновешенном и неуравновешенном.

М ост.

Т ермометр сопротивления.

Автоматическая система управления (АСУ) — это система представляющая собой совокупсность объекта управления и управляющего устройства взаимодействующая без участия человека.

Автоматическая система управления (АСР) аналогично.

Автоматизированная система управления — это человекомашинная система часть функций которой выполняет человек(чаще приниятие решений) выполняет человек.

В зависимости от объекта управления различают АСР тоесть локальные системы когда объектом является аппарат, машина, какой либо механизм.

АСУТП — это автоматическая структура управления технологическим процессом.

АСУП — это автоматическая структура управления предприятием.

Для этих типов характерна общая характерная структура управления.

Л юбая система управления ручная или автоматическая обязательно содержит четыре элемента, или четыре множества элементов, объединённых в замкнутый контур передачи информации. Это объект управления, управляющая часть, датчик, исполнительное устройство.

Датчик — это устройство или комплекс устройств преобразующее измеряемый параметр в удобный для передачи вид.

Управляющая часть это устройство или комплекс устройств реализующих алгаритм управления.

Управляющее устройство — это устройство осуществляющее воздействие на объект управления для поддержания требуемого режима работы.

Регулятор — это устройство или комплекс устроств обеспечивающее автоматическое поддержание заданного значения регулируемой величины.

Исполнительное устройство — это устройство или комплекс устройств для реализации управляющих воздействий.

Датчики и исполнительные устройства не меняют информацию, а лишь меняют вид энергии информации.

Изменение информации происходит в объекте и / или управляющей части.

Принцыпы управления.

В основе построения систем управления лежат общие принцыпы упрвления определяющие какую информацию использует управляющее устройство для формирования управляющего воздействия. Управление может быть по задающему воздействию, по возмущающему воздействию, по отклонению и комбинарованное.

П о задающему воздействию. В такой системе управления используется информация только о цели регулирования или значение заданного параметра. Для такой структуры характерна разомкнутая цепь воздействия, тоесть управляющее устройство воздействует только на объект, обратное воздействие отсутствует. Ещё такую систему называют разомкнутой системой управления.

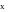
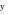
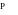
Достоинство — простая конструкция. Применяется когда свойства объекта известны и постоянны.

Системы с управлением по возмущению, работают по информации о возмущающем воздействии.

Управляющее устройство компенсирует влияние возмущающих воздействий. Ещё называется компенсирующей схемой.

Необходимо правильно выбрать тип возмущения. Используется при постоянных известных параметрах объекта. Разомкнутая схема.

Достоинства быстродействие, возможность практически полной компенсации возмущения, отсутствие проблем связанных с устойчивостью. Недостатки учитываются не все возмущения, не контролируется результат возмущающего воздействия, необходима надёжная информация о связи возмущающего воздействия и регулируемого параметра.

Управление по отклонению изспользуется информация о цели и отклонении текущего значения управляемого параметра от заданного занчения.

Сумматор — суммирует входящие сигналы, сигнал в заштрихованную часть вычитается.

Управление осуществляется как по прямой связи, так и по обратной.

Схема называется управлением с обратной связью, обратная связь может быть как положительной так и отрицательной.

е — это ошибка управления или регулирования. е = х - у, тоесть разность между предписанным и измеренным значением величины.

АСР — автоматическая система с замкнутой цепью воздействия в которой управление вырабатывается в результате сравнения истинного (измеренного) значения с заданным.

Данная схема справедлива как для автоматического, так и для ручного управления. Достоинства такого способа: учитываются все возмущающие воздействия, требуется минимум информации о процессе.

Недостатки: такое управление осуществляется методом проб и ошибок, второй недостаток — наличие запаздывания, при определённом сочетании свойств объекта и системы ( к примеру регулятора) система может стать не устойчивой.

Комбинированный вид управления. Для него характерно использование информации о возмущающем воздействии, направляющем воздействии и состоянии системы.

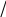
Такие системы имеют более высокое качество управления, чем системы по отклонению. Такая система обладает точностью и быстродействием. Применение таких систем ограничено тем, что не всегда известны параметры возмущающего воздейсвтия.

Классификация АСР.

Есть множество признаков по которым можно классифицровать. Важность того или иного признака зависит от задачи управления.

1. По назначению или по характеру изменения задания.

1. Стабилизирующие — это системы, алгоритм функционирования которых содержить предписания поддерживать величину на постоянном значении. х = const.

2. Програмные — это системы, алгоритм функционирования котороых содержит предписания измениять регулируемую величину по какому либо закону к примеру х = f(t).

3. Следящие — это системы, алгоритм функционирования которых содержит предписания изменять регулирующую величину в зависимости от заранее не извесной величины на выходе х. К следящим ссистемам можно отнести регулирование расходов двух веществ.

2. По количеству контуров.

1. Одноконтурные: содержат один контур управления.

2. Многоконтурные: содержат несколько контуров управления.

3. По числу регулиремых величин.

1. Одномерные.

2. Многомерные.

1. Системы не связанного регулирования, тоесть регуляторы у таких систем непосредственно не связаны, и могут воздействовать друг на друга только через общий объект управления.

1. Зависимые системы. К примеру температура и давление как параметры регулирования.

2. Не зависимые системы.

2. Связанные системы, в таких системах регуляторы связаны вне объекта.

4. По функциональному назначению.

5. По характеру используемых для управления сигналов.

1. Непрерывные, то есть контроллер или регулятор непрерывно изменяет управляющее воздействие, в зависимости от воздействия или от управляемой величины.

2. Дискретные, то есть управляющее воздействие принимает одно из нескольких возможных значений — релейные, импульсные и цифровые.

6. По характеру математических соотношений.

1. Линейные.

2. Не линейные.

7. По виду используемой энергии.

1. Пневматические.

2. Гидравлические.

3. Электрические.

4. Механические.

8. По наличию внутреннего источника энергии.

1. Системы прямого управления или регулирования, в них первичный измерительный преобразователь(датчик) воздействует непосредственно на изменение положения регулирующего органа.

2. Не прямого или косвенного управления. В таких системах применяются вспомогательные устройства работающие от сторонних источников энергии.

9. По принцыпу региулирования.

1. По заданию.

2. По отклонению.

3. По возмущению.

4. Комбинированные.

10. По виду зависимости ошибки от внешнего воздействия.

1. Статические. В таких системах при воздействии стремящемся со времянем к какому то постоянному значению, ошибка тоже стремится к постоянному значению, зависящему от величины внешнего воздействия.

2. Астатические. В таких системах, если воздействие стремится к какому то постоянному значению, ошибка стремится к нулю, вне зависимости от величины воздействия.

Классификация элементов систем.

Все системы управления состоят из отдельных элементов, и эти элементы так же классифицируются по некоторым признакам.

1. По функциональному назначению.

1. Измерительные.

2. Усилительно преобразовательные.

3. Исполнительные.

4. Исполнительные.

5. Корректирующие.

2. По виду энергии используемой для работы. Аналогичные такому пункту в прошлом списке.

3. По наличию или отсутствию вспомогательного источника энергии.

1. Активные.

2. Пассивные.

4. По характеру математических соотношений.

4.1 Линейные и нелинейные.

4. По поведению в статическом режиме.

1. Статические.

2. А статические.

Функциональная структура АСУ.

Исполнительное устройство. Чаще всего оно представлено двумя составляющими: исполнительный механизм и регулирующий орган. Исполнительный механизм предназначен для усиления мощности командного сигнала от регулятора и воздействия на регулирующий орган. В качестве исполнительного механизма может быть использован двигатель, сервопривод, сервомеханизм.

Регулирующий орган это техническое средство для изменения материального или энергетического потока влияющего на регулируюмую величину. Регулирующий орган не посредственно воздействет на объект. Как пример — вентили, клапаны, задвижки.

Датчик может состоять из нескольких элементов: нормирующий преобразователь и первичный измерительный преобразователь, чаще первичный измерительный преобразователь.

Первичнчый измерительный преобразователь — это устройство предназначенное для преобразования регулируемого параметра в какой либо сигнал в форме удобной для передачи и преобразования. К примеру термометр сопротивления или термопара.

Нормирующий преобразователь — это устройство для взаимного согласования входящих в систему управления элементов и дистанционной передачи синалов.

Функциональная структура АСР может быть представлена в двух вариантах. По каналу задающего воздействия. По каналу возмущающего воздействия.

Основы теории автоматического управления.

Работу системы управелиния можно описать словесно. Словесное описание помогает понять принцып действия системы, её назначение, особенности функционирования, но не даёт количественных оценок качества регулирования. По этому словесное описание не пригодно для изучения характеристик систем, для проэктирования систем. По этому была введена теория автоматического управления, которая рассматривает общие принцыпы построения систем автоматического управления, и закономерности протекающих в них процессов. Основы теории составляют математические описания. Основными задачами теории являются синтез и анализ систем.

Задача синтеза: построение системы управления с заданными свойствами. В результате решения определяют состав, структуру, параметры всех устройств входящих в систему.

Задача анализа: Исследование поведения системы с какими-либо свойствами в различных условиях.

В теории автоматического управлеиня используются точные математические методы описания свойств: дифференциальный уравнения, статические характеристики, динамические и временные характеристики, передаточные функции, частотные характеристики и другие. В теории автоматического управления вводят понятие звена, у которого есть определённые параметры, сигналы.

Динамизация систем узлов.

Объекты управления в биотехнологии характеризуются высокой сложностью, характеризуются не линейными дифференыциальными уравнниями высокой сложности получить общее решение которых сложно или нельзя. Чтобы уростить математическое описание, системы разделяют на отдельные элементы — динамические звения.

Динамическое звено — это математическая модель системы или элемента отражающая определённые динамические свойства вне зависимости от физической природы протекающих в нём процессов.

При анализе и синтезе систем управления их разбивают на элементы не по функциональному или конструктивному признаку а именно по динамическим свойствам. Диференциальное уравнение такого звена проще, чем уравнение всей системы, и решая эти уравнения мы можем найти решения для всей системы. Остаётся только учитывать взаимосвязь входных и выходных параметров этих звений.

Дифференциальный уравнения и их линеаризация.

Первый шаг в составлении динамики элемента — это выявление физического закона выявляющего его поведение.

Второй шаг — это определение(выявление) факторов от которых зависят переменные входящие в дифференциальные уравнения. Такой метод применим только в некоторых случаях(чаще всего процессы связаны не линейно). Для случаев не линейной связи учитывают что отклонения величин малы, и возможна замена не линейных уравнений линейными, тоесть возможность линеаризации.

Самый простой метод — графическая.

Математической основой метода линеаризации является разложение непрерывной функции дифференцируемой в окресностях точки соответствующей заданному режиму работы системы в ряд тейлора. С ограничением его линейными членами.

dF/ dx * дельтах + dF/dy * дельта игрек = 0.

Статические характеристики.

Статическая характеристика — это зависимость установившихся значений выходной величины от значения величины на входе системы.

y_уст = f(x).

Линейный статический элемент — это элемент обладающий линейной статической характеристикой, и не обладающий инерционностью. Линейные статические характеристики удобны для изучения так как они простые. Если модель элемента не линейная, то её преобразуют к линейному виду путём линеаризации.

Динамические характеристики: все системы управления являются динамическими, по этому их качесвто оценивается по поведению в двух режимах работы: установившемся, часным случаем которого является статический режим и не установившемся или переходном или динамическом.

Установившийся режим — это реакция системы остающаяся спустя большой промежуток времяни с момента изменения воходного сигнала. В таком режиме решаются две основные задачи: согласование диапозонов изменения элементов и определения коэффициента усиления управляющего устройства. Переходный режим характеризуется переходом системы из одного состояния в другое. Для этого режима формулируются показатели качства управления, составляется математическое описание прцоессов, решается задача синтеза, выполнятется анализ и даётся оценка работы системы.

Статическому режиму соответствует уравнение статики системы.

Переходному режиму соответствует уравнение динамики системы.

Преход системы из одного установившегося режима к другому при любых входных воздействиях называется переходным процессом. Переходные процессы изображаются графическитв виде графика зависимости у от t.

Динамика характеризует поведение системы.

Следует различать динамические характеристики и статические.

Зная набор динамических характеристик, можно построить статическую характеристику, но по статической характеристике построить динамику не возможно.

Преобразования Лапласа.

Исследование систем управления существенно упрощается при использовании прикладных математических методов операционного исчисления, по скольку позволяет от решения дифференциальных уравнений перейти к решению алгебраических уравнений.

Операционный исчисления — это один из методов математического анализа для решения сложных задач.

В основе метода лежит замена изучаемой функции (ориганалов) некоторыми другими функциями (изображениями) получаемых по определённым правилам. Одно из таких преобразований носит название преобразования Лапласа.

Преобразование Лапласа — это математический метод позволяющий довольно просто решать линейные дифференциальные уравнения. В результате преобразования диференциальные уравнения в пространстве оригиналов приобретают форму алгебраического уравнения в пространстве изображений, в котором в качестве независимой переменной вместо времени t, используется комплексная переменная S

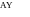
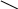
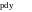
D Y

Некоторые преобразования Лапласа действительной переменной f(t)

F(s) = L[f(t)] = нтеграл от ноля до бесконечности f(t)*(e^(-st)) * dt

Были разработаны таблицы в которые сведены наиболее часто встречаемые функции и их оригиналы. Эти таблицы позволяют избежать непосредственного использования формул.

Ориганал	изображение
d(t) d здесь — дельта — импульс.	1
1(t)	1/S
T	1/s^2
t^n	N!/(S^(n+1))
e^(-c*t)	1/(S+с)
(d^n)/(d * t^n)	S^n
dt	1/s
x(t)	X(s)
y(t)	y(s)

Свойства преобразований Лапласа.

1. Они линейны.

Если функции f1(t) и f2(t), являются оригиналами, изобрежаения которых F1(s) и F2(s) соответсвтенно и величины с1 и с2 не зависят от t и комплексной переменной s, то справедливо равенство

L[c1 * f1(t) + c2*f2(t)] = c1* F1(s) + c2 * F2(s)

2. Дифференцирование оригинала.

Если функция f(t) и её производная степени n f^n(t), являются оригиналами, то справедливо равенство

L[f^(n)(t)] = S^n * F(s) – S^n-1 f(0) - …. - S^-2 * f(0) – f^n-1(0)

Это свойство позволяет переводить решение диференциальных уравнений в решение алгебраических.

3. Интегрируемость.

L[нтеграл от 0 до t функции f(t)dt] = F(s)/S.

4. Теорема запаздывания.

L(f(t-c)] = F(s) * e^-ct

5. Теорема смещения.

L[f(t)* e^ct] = F(s-c)

6. Начальные и конечные условия.

Чтобы упростить решение большинства задач управления, дифференциальные уравнения записывают в отклонениях от режима выбранного подходящим образом, то есть номинальным, что приводит к нулевым начальным условиям.

Начальные условия — это совокупность переменных величин процесса к примеру температура, концентрация и некоторого числа их производных в начальный момент времени.

Нулевые начальные условия — переменные величины и их производные равны нулю в начальный момент времени.

Не нулевые начальные условия — если хотябы одно значение из переменных или их производных не равно нулю.

Передаточные функции.

Преобразование Лапласа даёт возможность ввести удобное понятие передаточной функции, характеризующей динамические свойства системы.

Передаточная функция показывает: какое действие совершает звено над входным воздействием, другими словами: как изм+ Y(s) = 2 * s * x(s) + 4 * x(s)

Y(s)(3s^2 + 4s + 1) = x(s)(2s+4)

W(s) = Y(s)/(X(s)) = 2 * s + 4/(3s^2 + 4s +1)

Y(s) = W(s) * X(s)

Y(t) = f(x(t))

Передаточной функцией звена или системы называется отношение изображения выходного воздействия к изображению входного, при нулевых начальных условиях.

Так, как передаточная функция полностью определяет динамические свойства системы, первоначальная задача — определение передаточной функции.

Введение передаточной функции позволяет:

1. определить динамические свойства системы или звена;

2. перейти к частотным характеристикам, а с их помощью определить усточивость системы и другие её характеристики;

3. определить тип звена.

Передаточные функции устойчивых динамических систем обладают следующими свойствами.

1. Передаточная функция представляет собой дробно — рациональную функцию следующего вида: (b₀ + b₁s + b₂s² …. b_ms^m)/(a₀ + a₁s + a₂s² + …. + a_nsⁿ).

2. n всегда больше m. Все постоянные коэффициенты действительны.

3. Приравняв полином знаменателя к нулю, получим характеристическое уравнение системы, которое обычно обозначают D(s) = 0.

Корни этого уравнения называют полюсами передаточной функции.

4. Корни полинома числителя называют нулями передаточной функции.

5. Не действительные нули и полюсы могут быть лишь комплексно сопряжёнными.

6. Если все полюсы расположены в левой полуплоскости комплексной плоскости, то система устойчива.

7. Если S = 0, то передаточная функция системы превращается в обычнй коэффициент усиления.

8. Передаточная функция системы определяется как отношение полинома правой и левой частей диференциального уравнения.

Временные характеристики.

Временной характеристикой называют закон изменения выходной величины звена или системы во времяни в ответ на изменение входного воздействия, при условии, что до этого звено система находилась в покое.

О динамических свойствах системы судят по её реакции к одному из типовых видов сигнала.

Так, как входные воздействия могут быть различными, по разному изменяться во времяни, то и переходные(временные) характеристики каждый раз будут разными.

Для простоты анализа все входные воздействия приводят к одному из типовых видов, и в зависимости от вида входного воздействия, функция y(t), тоесть выходное воздействие(выходной сигнал), может иметь разное обозначение и разное название.

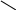
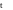
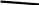
С уществуют 4 основных типа сигнала

названия для графиков с лева на право — единичной ступени, дельта функция или функция импульса, линейный или рамповый, гармонический; частотная функция.

Импульсная переходная функция — это аналитическое выражение отклика звена на единичное ступенчатое воздействие, при нулевых начальных условиях.

h(t)=L^-1[W(s) * 1/S]

Y(s) = W(s) * X(s)

график — рисунок, характеристика — функция.

График изменения выходного сигнала при ступенчатом входном воздействии отличающемся от единичного, называют обычно кривой разгона.

Импульсная переходная характеристика или функция веса — это аналитическое выражение отклика звена на единичное ступенчатое воздействие при нулевых начальных услвоиях.

W(t) = L^-1[w(s)*1].

Рамповая характериситка — это аналитическое выражени отклика звена на единичное рамповое воздействие.

y(t) = L^-1[w(s) * 1/S^2].

Частотная характеристика — это реакция системы на гармоническое входное воздействие.

Частотные характеристики снимаются в установившемся режиме.

Частотные характеристики позволяют определить тип регулятора приемлимого в данной системе, и решить задачу об устойчивости системы.

По частотным характеристикам, так же, можно судить о временных характеристиках.

Если на вход системы, звена или объекта подаётся гармонических синусоидальный сигнал с частотой W и амплитудой Авх

Х(t) = Ав * sin(Wt),

то после завершения переходного процесса, в установившемся режиме выходная величина будет совершать вынужденные гармонические колебания

y(t) = Авых * siin(W * t + фи)

с той же частотой, но другой амплитудой, но сдвинутые по фазе на угол фи.

АЧХ Авых/Авх = f(w)

ФЧХ Фи = f(w).

Определяя в установившемя режиме отношение амплитуд и фазовый сдвиг при разных частотах колебаний входного сигнала, можно экспериментально получить частотные характеристики, и в связи с этим выделяют несколько частотных характеристик.

А(w) = Авых/Авх иногда величину A(w) обозначают как А.

Отношение амплитуд от частоты колебаний называется амплитудной частотной или амплитудо -частотной характеристикой (АЧХ).

ФЧХ

АФЧХ — амплитудная фазовая частотная характеристика.

Частотная передаточная функция.

Реакцию системы на гармоническое входное воздействие, можно не только определить экспериментально, но и рассчитать достаточно точно, если известно математическое описание системы — тоесть передаточная функция и дифференцыиальные уравнения.

Используя преобразования Лапласа, можно найти изображения входного сигнала

Х(s)=L[Авх*sin(Wt)] = Авх*w/(s^2 + W^2)

Y(s) = W(s) * X(s).

у(t) = L'[Y(s)].

Для определения установившейся реакции звена, с передаточной функцией

w(s) на гармонический входной сигнал, достаточно знать комплексную функцию w(jW)

w (s) - w(jw) = Y(jW)/X(jW)

s = jw.

Передаточная функция по Фурье так же, характеризует передаточный свойства функции, не зависит от внешнийх воздейсвтий. С её помощью можно определить реакцию системы на любой сигнал. Главное, что бы этот сигнал можно было преобразовать по Фурье. Эту функцию можно представить в виде суммы действительной и мнимой части.

w(jw) = Re)(W) + Im(W).

Между действительной, мнимой частью, а так же АЧХ и ФЧХ, есть взаимосвязь.

А(W) = (Re^2(W) + (Im)^2(W))^(1/2)

Фи(W) = atctg(Im(W)/Re(w))

Re(W) = А(w) * cosфи(w)

Im(w) = А(w) * sinФи(W).

Для каждого фиксированного значения частоты, частотная передаточная функция может быть изображена на комплексной плоскости радиус-вектором, длина которого соответствует A(W), а угол = фи(W), при этом положительное направление против ЧС, 0 на оси действительных чисел.

Эти функции вводили для того, что бы определять частотные характеристики теоретически.

АФЧХ, ФЧХ, АЧХ могут быть изображены графически.

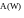
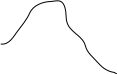
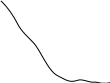
А ФЧХ изображается на комплесконой плоскости, иногда е называют диагрммой Найквиста, представляет собой годограф частотной передаточной функции, при измененеии частоты от ноля до бесконечности.

Годограф это траектория движения конца радиус-вектора.

АЧХ и ФЧХ, их изображения не нашли применения так, как их изображения не удобным и малоинформативны.

Чаще используют логорифмические частотные характеристики.

Логорифмическая АЧХ.

График разбивается на декады.

L(W) = 10lg((A^2)(w)) = 20lg(A(W)).

ЛФЧХ.

Логарифмические характеристики строятся либо раздельно, либо в виде совмещённой диаграммы(диаграмма Боде).

Структурные схемы.

Структурной схемой называют графическое изображение математической модели системы в виде соединения звеньев. Звено на структурной схеме изображается в виде прямоугольника с указанием входных и выходных величин и передаточной функции внутри него.

Сколько бы не была сложна системы, её можно изобразить используя три основных типа соединения звеньев: последоватльное, параллельное, с обратной связью.

Последовательное соединение.

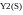
Входная величина каждого последующего звена является выходной величиной каждого предыдущего.

Параллельное соединение.

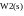
Соединение с обратной связью: считают, что звено связано обратной связью, если его выходное воздействие подаётся на его вход через какое либо другое звено. При этом звения образуют замкнутый контур, или замкнутую цепь.

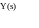
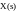
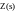
W(s) = w1(s)/ (1-/+ w1(s))

Эквивалентные преобразования.

При синтезе систем управления, необходимо выполнять преобразования структурных схем, для упрощения конечной структуры, и приведения её к виду удобному для работы. Следует иметь в виду, что разработанные инженерные методы определения основных характеристик систем рассчитаны на стандартный вид структурной схемы.

Определив исходную схему в виде типовых звеньев, которые соединены определённым образом, найдя их передаточные функции, необходимо идти по пути последовательного упрощения исходной схемы, приводя её к стандартному виду по правилам эквивалентного преобразования.

Правила эквивалентного преобразования на самостоятельное изучение.

Зная структуру и параметры системы, находят передаточную функцию системы, а затем её(системы) дифференциальное уравнение.

Замкнутая и разомкнутая системы.

Если выход системы подавать на её вход, то это замкнутая системы, если не подавать то разомкнутая система.

Для разомкнутой системы

wp или wбеск(s) = wp * woy.

(s) = wбеск(s) / (1+/- wбеск(s) — для разомкнутой системы.

з

Данная передаточная функция, которая определяет зависмость y от х, называется передаточной функцией замкнутой системы по каналу задающего воздействия.

(s) = E(s)/X(s) = 1/ (1 +/- wбеск(s))

Е

(s) = Y(s)/F(s) = Wв(s) / (1 +/- wбеск(s))

В

wв(s) — это передаточная функция по каналу передачи возмущения.

wбеск = В(s) / А(s).

= В /(А+В) = В / D

з

= А / (А+В) = А / D.

Е

А(s) + В(s) = D(s) — это характеристическое уравнение замкнутой ситсемы.

Достаточно найти wбеск = w1 w2 * В/А.

А(s) — это характеристическое уравнение для размокнутой системы.

Типовые динамические звенья.

Динамические звенья назыают типовыми, если изменения проходящего через них сигнала, можно описать уравнением(алгебраическим или дифференциальным) не выше второго порядка. Чаще всего это бывает линейдное дифференциальное уравнение.

а2 d^2y/(dt^2) + a1 dy/dt + a0y = b2 d^2x/dt^2 + b1dx/dt + b0x.

w(s) = a2 s^2 + a1s + a0/(b2s^2 + b1s + b0)

w(s) = e^(-tзапS)

Классификация типовых звеньев.

По порядку уравнени.

• 0 (a2 ;a1; b2; b1 = 0)

• 1 (a2; b2 = 0)

• 2

В зависимости от поведения в установившемся режиме.

Статические.

В статическом режиме входной и выходной сигналы связаны между собой взаимно однозначной функцией. Эта функция называется выходной характеристикой.

y = k*x

k — это статический коэффициент усиления.

b0 не равно; а0 не равно 0.

Интегрирующие или астатические.

У таких звеньев выходной сигнал, в установившемся режимие, пропрорционален интегралу по времяни от входного сигнала.

b0 не равен 0; а0 = 0

Дифференцирующие или форсирующие.

У таких звеньях, выходной сигнал пропроционален производной от входного сигнала. b0 = 0; а0 не равно 0.

В зависимости переходного прцесса.

Звенья могут быть апериодические, колебательные, консервативные.

Кроме данных классификаций, звенья разделяют так же на устойчивые и не устойчивые; инерционные и безинерционные(идеальные); минимальнофазовые и не минимальнофазовые.

y — выходной сигнал;

х — входной сигнал;

t — время.

Статическое звено нулевого порядка, так же его называют безинреционным, усилительным, пропрорциональным.

Звено называют статическим нулевого порядка, если его входная и выходня величины связаны зависимостью

у(t) = к * х(t).

Пример — рычаг, механические передаточные механизмы: регулирующие клапаны.

Передаточная функция является постоянной величиной

w(s) = к.

к — коэффициент пропорциональности.

При подаче на вход звена единичного ступенчатого сигнала оно передаёт сигнал мнгновенно, без искажений и запаздывания, наблюдается только изменение масштаба. Масштаб зависит от коэффициента к, тоесть может быть увеличение или уменьшение масштаба.

Переходная функция

h(t) = l'[w(s)/s] = к

Переходная характеристика.

Импульсная переходная функция.

w(t) = к * дельта(t)

Рамповая переходная функция.

g(t) = k(t)

Частотная передаточная функция.

w(jW) = к = (к^2 + 0^2)^(1/2)

А(W) = к

к * Re + Im * 0

Фи(w) = 0

Сигнал любой частоты поступающий на вход звена усиливается в одинаковой мере без какого либо фазового сдвига.

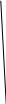
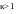
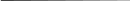
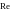
Статическое звено первого порядка.

Звено называется статическим первого порядка или устойчивым или устойчивым или апериодическим, если его входная и выходная величины связаны между собой дифференциальным уравнением вида

a1 * dy/dt + a0y = b0x

Если поделим всё уравнение на f0 и обозначим T = a1/a0, к = в0/а0.

к — это коэффициент пропорциональности звена.

t — постоянная времени.

Как находится постоянная времяни прочитать самостоятельно.

Примеры такого звена RC фильтр; термопара, термометр расширения, ёмкость с сжатым газом и другие.

Передаточная функция

W(S) = к/(T*S + 1).

Переходная функция.

h(t) = к*(1 — e^(-t/T))

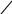
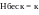
Время для достижения нового установившегося значния, теоретически, бесконечно, по этому звено называют инерционным.

Физический смысл постоянной времяни — определяет динамические свойства звена — это мера инерционности звена.

Чем больше постоянная времяни, тем медленнее протекает переходный процесс, и тем более пологая экспонента. Допустим, что T стремиться к нолю. Получается, что можно получить звено нулевого порядка из звена первого.

Геометрически, постоянную времяни, можно определить, как проекцию на ось времяни отрезка касательной к экспоненте, заключённой между точкой касания и точкой пересечения касательной с линей установившегося значения.

Геометрический смысл постоянной времяни можно определить при t = 0, тоесть постоянная времяни — это время, в течение которого, выходня величина достигает нового установившегося значения, если она меняется с постоянной скоростью, равной начальной.

Переходная характеристика звена обладает следующими свойствами:

• новое установившееся значение на выходе равно статическому коэффициенту.

• в точке х = 0(в начальынй момент), скорость изменения выходной величины = к/t

• касательная к кривой в точке t = 0 пересекает асимптоту(установившееся значение) в точке, когда t = T.

• величина под касательной равна T, и не зависит от точки проведения касания.

• за время t = T, выходная величина достигает 63% от своего установившгося значения.

В инженерных расчётах считается, что время переходного процесса звена приблизительно равно 4* Т, тоесть через 4Т считается, что достигается установившееся значение.

Импульсная переходная функция.

w(t) = (к/Т) * e^(-t/T)

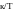
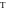
y (t) = кT * (e^(-t/T) + t/T – 1)

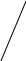
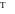
Частотная функция.

w(s) превратили w(jW) = к/(ТjW + 1) * (-TjW + 1)/(-TjW + 1) = к(1 — ТjW) / (1 + T^2 * W^2)

Im = кTW/ (1 + T^2 * W^2).

А(W) = к/(1 + Т^2 * W^2)^(1/2)

Фи(w) = - arctg(TW)

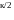
Звено запаздывания.

Для любого устройства, естественно некоторое запаздывание выходной величины на некоторое время относительно момента поступления информации на его вход. Определение запаздывания самостоятельно.

Звено запаздывания — это звено, которое не изменяет вид входного сигнала, точно его повторяет, лишь задерживает во времяни этот сигнал к примеру транспортёр (расход сырья — сигнал задерживается на время прохождения сырья через транспортёр)

y(t) = х(t – tзап).

Явление запаздывания имет место, когда возмущающее воздействие, распространаясь с конечной скоростью, вызвает изменения управляемого параметра лишь спустя некоторое время. Если на вход звена запаздывания подавать гармонический сигнал, х(t) = Авх * e^(jWt), то спустя время, равное времяни запаздывания, на выходе появляются колебания той же частоты, но с другой амплитудой

y(t) = Авых * e^(jw(t – tзап))

w(jw) = e^(-jWtзап)

w(s) = e^(-stзап).

A(W)

ф и(W)

Статическое звено второго порядка — звено, в котором воходная и выходная величины связаны линейным дифференциальным уравнение второго порядка.

a2d^y/dt^2 + a1dy/dt + a0y = b0x

к = в0+а0 — коэффициент усиления.

Т^2 = а2/а0 — постоянная времяни

2зетаТ = а1 / а0 — коэффициент демпфирования

Т^2 * d^2y/dt^2 + 2зетаТdy/dt + y = к * х.

В зависимости от коэффициента демпфирования различают разные типы:

зета >1 апериодические к примеру ректификационаня колонаа

0<зета<1 U-образный дифманометр, исполнительный механизм, RCL фильтр.

Зета = 0 — консервативное

зета = 1 — критическое демпфирование.

1/w0^2 * d^2y/dt^2 + 2зета/W0 * dy/dt + y = кх

w(s) = к / T^2s^2 + 2зетаTS + 1.

Характер переходного процесса будет определяться корнями характеристического уравнения

T^2 * s^2 + 2зетаТS + 1 = 0

s1,2 = (-зета +/- (зета^2 — 1)^(1/2))/Т

h(t) = L^-1[к/(Т^2 * s^2 + 2зетаТs + 1 * 1/s] = L^-1[к/(Т^2(s + альфа1)(s + альфа2) * 1/S)]

Несколько случаев оригинала по его изображению.

Зета > 1, то оба корня характеристического уравнения действительные и отрицателные: s1 = - альфа1; s2 = - альфа2.

После преобразований по Лапласу, при условии, что альфа1 не равно альф 2, то h(t) = 1- альфа2/(альфа2 — альфа1) * e^^{-альфа1 t} + альфа1/(альфа2 — альфа1) * e^(-альфа2t).

Если зета = 1, то s1,2 = - 1/Т = - альфа.

h(t) = L^-1[к/(т² * (s + альфа²))]

еси 0< зета<1 есть два сопряжённых комплексных корня.

S1,2 = -зета/Т +/- j * (1-зета^2)/Т = альфа +/- j Бета

h(t) = L^-1[(к / T^2 (s + альфа)^2 + Бета^2) * 1/s]

зета = 0, уравнение имеет два сопряжённых мнимых корня, s1,2 = +/- j/T.

h(t) = L^-1[к/(Т^2S^2 + 1) * 1/s]

h(t) = (1 – cost/t) * К = К(1 – cosW0t)

Тоесть, сигнал будет представлять собой незатухающие колебания с частотой w0 и амплитудой К.

При коэффициенте демпфирования от 0 до 1, выходной сигнал будет совершать затухающие колебания — слабодемпфированная система.

При коэффициенте = 0, выходной сигнал представляет собой незатухающие колебания — не демпфированная система.

Если коэффициент = 1, имеет место критическое демпфирование, система приходит к состоянию равновесия, без колебаний, за максимально возможное время.

Если коэффициент больше 1, то колебательный процесс отсутствует, система приходит в равновесие тем медленнее, чем больше коэффициент — сильно демпфированные системы.

w(jW) = w(s)

S = jw

Re(w) = К(1 – T^2 W^2) / ((1 — Т^2 * W)^2 + 4зета^2 T^2 W^2)

Im(w) = - 2T * зета * К * W.

А(W) = К/(1 — T^2 * W^2) + 4 зета^2 * Т^2 * W^2)^(1/2)

фи(W) = - arctg (2ТзетаW/(1 — T^2 w^2)).

Интегрирующее звено.

Идеальное интегрирующее звено

Звено называют интегрирующим, астатическим, нейтральным, если скорость изменения выходной величины пропорциональна входной величине.

Та = dy/dt = х

Та — постоянная времяни интегрирования.

У = 1/Та * интеграл от 0 до t (хdt). Примеры: поршневой исполнительный механизм, двинатель постоянного тока.

h(t) = 1/Та * t.

При не большом изменении входного взена, выходной сигнал интегрирующего звена начинает изменяться с постоянной скоростью, и ни когда не достигает нового установившегося состояния.

w(jW) = 1/(ТаjW) = - 1/ (Ta * W) * j

А(W) = 1/(Та * W)

фи(W) = - Пи/2

Реалное интегрирующее звено.

Т * Та * d^2 y/dt^2 + Ta * dy/dt =x

Та — постоянная времени интегрирования.

Т — постоянная времени звена.

w(s) – 1/(T0 * S * (T * S + 1)

Т = 0

Чем меньше значение Т, тем идеальнее звено.

Идеальное дифференцирующее звено.

Считается, что идеальных дифференцирующих звеньев не существет

Звено называется идеальным дифференцирующим, если его выходня величина пропорциональна скорости изменения входной величины, к примеру тахогенеретор.

У = Тd * dx/dt

Тd — это постоянная времяни дифференциирования.

w(s) = Td * S

h(t) = Td * S

w (jW) = jW * Td

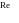
А 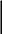(W) = Тd * W

Ф и(w) = Пи/2

Реальное диффиренцирующее звено

Т * dy/dt + у = Тd(dx/dy)

Диффиренцирующие звенья вводят для кооректировки динамических свойств системы(они улучшают упрвление).

Пример CR цепь(электрическая) u = f(u);

Передаточная функция.

W(s) = Т * ТdS/(TS + 1)

h(t) = Td/T * e^(-t/T)

w(jW) = TdjW/(TjW + 1) * (TJW-1)/ (TjW – 1)

Re = TdTW^2 / (1+T^2 * W^2)

Im = Td * W / (1 + T^2 W^2)

А(W) = TdW/(1 + T^2 * W^2)^(1/2)

w(jW) = Re + Im(W).

Неустойчивое звено первого порядка.

Tdy/dt – y = Kx

W(S) = K/(TS – 1)

h(t) = K(e^(t/T) – 1)

w(S) = K/(Ts - 1)

h(t) = K(e^(t/T) – 1)

Re = K/(T^2 * W^2 + 1)

Im = - KTW/(T^2 * W^2 + 1)

A(W) = K/(T^2 * W^2 + 1)

фи(w) = -arctg(tW)

W(jW) = K(TjW – 1)

Устойчиость линейных систем.

Под усточисостью понимают способность системы автоматического управления восстанавливать своё состоянине равновесия после устранения возмущающего воздействия.

Устойчивые системы возвращаются в исходное состояние равновесия, если устраняется возмущающее воздействие, или переходят в новое состояние, если возмущающее воздейтвие было ступенчатым.

Переход в устойчивое состояние, может быть апериодическим, либо путём затухающих колебаний.

П осле устранения возмущающего воздействия неустойчивые системы апериодически удаляются от состояния равновесия, или совершают расходящиеся колебания.

После устранения возмущающего воздействия нейтральные системы приходят в состояние равновесия отличающего от начального, или совершают незатухающие колебания.

Устойчивость является одним из главных требований к системам управления, так, как определяет её работоспособность. Работать может только устойчивая система.

Что бы определить устойчива ли какая либо система, изучают поведение этой системы, при малых отклонениях от положения равновесия.

Поведение любой линейной стационарной системы, при наличии внешних значения, можно описать не однородным дифферецниальным уравнением, и соответсующей ему передаточной функции.

При этом получаем уравнение вида w(S) = полином/полином

Решение такого уравнения, можно представить в виде суммы двух составляющщих.

у(t) = yуст(t) + упер(t).

Определив все корни этого характеристического уравнения, общее решение однородного дифференциального уравнения, можно привести к степенному выражению.

yпер(t) = с1у^s1t + с2e^s2t + .. + сn-k * e^sn-k t + (Ck10 + Ck1t + ck,k-1 tk^-1) * e^skt

S = 0

S = альфа

S = альфа +/-jбета

Корни характеристического уравнения, определяют устойчивость системы.

Линейная система устойчива, если все действительные корни и действительные части смешанных корней характеристического уравнения, отрицательны. Если, хотя бы один корень характеристичического корня, или вещественная часть одно из комплесных корней положителен, то система не устойчива.

Если характеристическое уравнение имеет только один нулевой корень, а все остальные корни имеют отрицательную вещественную часть, то такая система является нейтральной — устойчивой, тоесть она находится на апериодической границе устойчивости.

Если уравнение системы имеет только одну пару сопряжённых мнимых корней, а все остальные корни именют отрицательную вещественную часть, то такая система является нейтрально — устойчивой, тоесть находится на колебательной границе устойчивости. Если хотя бы один корень или вещественная часть положительна, то система не устойчива.

В действительности, почти всегда, мы имеем дело с нелинейными системами. Но параметры работы позволяют их линеаризовать, тоесть привести к линейному виду.

Теорема Ляпунова гласит, что если линейное приближение не линейной системы устойчиво, то и система может быть устойчива.

Ти — время изодрома; время удвоения.

Ти = Кр * Та

Физический смысл времени изодрома.

Время изодрома — это время, в течении которого регулирующий орган, под действием интегральной составляющей, переместится точно так же, как и под действием пропорциональной составляющей.

Время предворения

Тп = Тд/Кр

Показатели характеризующие быстродействие

tпп — это продолжительность переходного процесса от момента нанесения возмущающего или управляющего возедйствия, до достижения управляемым параметром нового установившегося значения с заданной точностью дельта. Часто точность задают как долю от yуст(y устновившегося).

Время переходного процесса в системах регулирования, называют времяем регулирования и стремяться его минимизировать.

tmax — время достижения первого максимума.

Стремяться tmax свести к минимуму.

Показатели, характеризующие колебательность. Используются только для колебательных процессов.

пси — степень затухания.

пси = (А1 — А3)/А1, где

Аn — соответствующая амплитуда колебания значения вокруг установившегся значения.

Если незатухающие колебания пси = 0

если расходящиеся колебания, то пси < 0.

Перерегулирование:

сигма = А2/А1 * 100%; сигма = (lmax – lбеск)/lбеск.

Обычно, системы настраиваются так, что бы перерегулирования составляло от 10% до 30%, обычно говорят о 20% перерегулировании.

Логарифмический декримент калебания:

дельта(буковой) = lg(А1/А2).

Колебательность. Колебательность системы можно охарактеризовать числом колебаний за время переходного процесса.

Если в системе, за время переходного процесса, совершено число колебаний меньше заданного, то система имеет требуемое качество.

Типовые оптимальные процессы регулирования.

Оптимальным процессом регулирования называют процесс, который соответствует минимуму или максимуму какого либо показателя качества регулирования. В зависимости от технологического процесса и от возмущающих возвдействий, наилучшими можно признать различные по своему характеру процессы. Из устойчивых переходных процессов, в качестве оптимального выбирают один из трёх.

1. Граничный апериодический процесс с минимальным времянем регулирования. Для граничного апериодического переходного процесса, характерно отсутствие перерегулирования, наименьшее воздействие управляющего устройства на объект и минимальное время регулирования. Наименьшее воздействие управляющего устройства приводит к наибольшей максимальной погрешности регулирования. Область применения — при значительном влиянии воздействия, которое является управлющим, на другие технологические величины.

2. Процесс с 20-и процентным перерегулированием и минимальным времянем первого полупериода колебаний. Для этого процесса, характеры большее упрвляющее воздействие и большее время регулирования, но меньшая максимальная погрешность. Область применения — при управлении объектами, допускающими перерегулирование. Первый полпериод колебаний является основным, здесь ошибка максимальна, влияние остальных полпериодов незначительно.

3. Процесс с минимальным значением интеграла от квадрата ошибки. Для данного процесса характерно наибольшее управляющее воздействие, наибольшее время регулирования и наименьшая максимальная ошибка, а так же значительное перерегулирование (до 40%). Область применения — для объектов, для которых максимальная погрешность должна быть как можно меньше.

Определение оптимальных параметнов настройки промышленных регуляторов.

Выбор того или ингого закона управления определяется в первую очередь, динамическими свойствами объекта, величиной и характером возмущающих воздействий, и показателями качества. Исходя из технологических требований, выбирают один из трёх типовых переходных процессов, в качестве заданного. Переходный процесс зависит от свойств объекта, от характера величины и места приложения возмущающих воздействий, от закона регулирования и параметров настройки регулятора.

Что бы достичь требуемого качество регулирования, требуется определить закон регулирования, и требуемые параметры регулятора.

Предворительным критерием выбора структуры системы и закона действия регулятора, может служить величина отношения времяни запаздывания объекта, постоянной времяни объекта.

Для нейтральных объектов(по сути инерционных), постоянную времяни объекта можно замести на постоянную инерционности (Та).

tзап/Т0, если это отношение меньше 1, то удовлетоворительное качество регулирования можно получить, используя одноконтурную систему регулирования. В зависимости от величины этого соотношения, можно предварительно выбрать закон регулирования. Если отношение меньше 0,2, то, при небольших изменениях нагрузки, можно использовать регулятор релейного действия. Если это соотношения больше 0,2 но меньше1, лучшее качество регулирования обеспечивают регуляторы непрерывного действия при чём, с ростом соотношения, следует усложнять закон.

Методы определени отпимальных параметров регулирования.

Метод незатухающих колебаний.

Метод последовательного приближения — это процедура сложная и трудоёмкая, возможны самые разнообразные комбинации параметров настройки, по этому используют достаточно простой метод незатухающих колебаний.

Значения параметров настройки достаточно близкие к оптимальным, можно получить, если исследовать замкнутую одноконтурную систему, с П — регулятором. Если используют время изодрома ставят максимально возможным. Время предворения стараются сделать самым малым, тоесть по сути мы приближаем любой регулятор к П — регулятору, и определяют реакцию системы на ступенчатые изменения управляемого парметра, при различных значениях коэффициента регулятора. Значение коэффициента усиления, при которой в системе возникают незатухающие колебания с постоянной амплитудой — это и есть максимальный коэффициент усиления. Период колебаний, в этом случае, называется предельным или критическим. Для определения этих настроек достаточно провести небольшое количество опытов. Данные значения подставляются в формулы для нахождения настроек регуляторов.

З-н	Кр	Ти	Тп
П	0,5 * Крmax	-	-
ПИ	0,45 * Крmax	Ткр/1,2	-
ПИД	0,6 * Крmax	Ткр/2	Ткр/8

Метод затухающих колебаний. Многие объекты не допускают даже кратковременной работы в режиме незатухающих колебаний. В этом случае используют метод затухающих колебаний, тоесть модификацию предыдущего метода.

Значения коэффициента усиления изменяют до тех пор, пока декремент затухания не будет равен 0,25. Рассчитывают значения Ти = Ткр/1,5; Тп = Т/6. После установки в регулятор значений Ти и Тп, уточняют значение коэффициента усиления.

В основу стандартизации ГСП положены следующие принципы: выделение основных функций контроля и регулирования; минимизация номенклатуры технических средств автоматизации; построение устройств на основе типовых унифицированных блоков и модулей; агрегатное построение сложных систем на основе унифицированных приборов и устройств; совместимость приборов и устройств (рассматривают три типа совместимости:

• информационная совместимость — унификация сигналов связи, используется для установления связей с другими устройствами;

• конструктивная совместимость, на пример применение одинаковых типов разъёмов;

• эксплуатационная совместимость (требования к температурному режиму, агрессивным средам, влажности);

• метрологическая совместимость — обеспечение единства единиц измерений).

По функциональному признаку, средства ГСП подразделяются:

• средства получения информации о состоянии процесса;

• средства приёма, преобразования и распределения сигнала по каналам связи;

• средства преобразования, обработки, хранения информации и формирования управляющих воздействий

• средства использования командной информации для воздействия на технологический процесс.

По роду энергии используемой в качестве носителя информации при передаче сигнала подразделяются:

• электрическая;

• пневматическая;

• гидравлическая.

Унифицированный сигнал — это сигнал дистанционной передачи информации с унифицированными параметрами (или со стандартными параметрами).

В зависимости от вида унифицированных параметров применяют сигналы четырхёх групп.

1. Сигналы тока и напряжения, электрические непрерывные.

2. Сигналы частотные, электрические непрерывные.

3. Сигналы электрические, кодированные.

4. Пневматические сигналы (объединяют и гидравлические и пневматические).

Электрические постоянный ток		Переменный ток напряжение	Частотные	Пневматические
мВ	мА	В	кГц	кПа
0 — 10	0 — 5	0 - 2	4 — 8	20 - 100
0 — 20	0 — 20	-1 — 0 — 1	2 - 4
- 10 — 0 — 10	4 — 20
	-5 — 0 — 5

Измерение физической величины — это совокупность операций по применению технического средства хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или не явном виде), с её единицей и получение значения этой величины.

Измерения можно классифицировать по разным признакам.

1. По характеру зависимости измеряемой величины от времени:

- статические — это измерения величины, которая принимается в течение времяни измерения постоянной;

- динамические — это измрения изменяющейся физической величины.

2. По способу получения результатов:

- прямое измерение — измерение, которое получается непосредственно;

- косвенные измерения — измерение значение одной физической величины происходит при измерении другой величины.

- совокупные измерения — одновременно измеряют несколько одноимённых величин, а искомые значения нужной величины находят решая уравнение или систему уравнений

- совместные измерения — это измерения, когда одновременно измеряются несколько разноимённых величин.

Средства измерительной техники.

Средство измерительной техники — это обобщающее понятие, охватывающее технические средства специально предназначенные для измерений. К ним относят: средства измерений, их совокупности (как пример: измерительные ситсемы; измерительные установки), измерительные принадлежности (как пример — термостат) и измерительные устройства.

Средство измерений — это техническое средство, предназначенное для измерений, имеющее определённые метрологические характеристики, воспроизводящее и/или хранящее идиницу физической виличины, размер которой принимают неизменным в течении известного интервала времени.

Мера физической величины — это средство измерений предназначенное для воспроизведения и/или хранения физической величины одного или нескольких заданных размеров, к примеру — гири. Далее они подразделяются на однозначные; многозначные; набор мер; мгазин мер.

Однозначная мера, на пример — одна гиря, содержит в себе эталон массы. Многозначная мера — это мера воспроизводящая физическую величину разных размеров.

Набор мер, на пример — набор гирь, набор отрезков - это комплект мер разного назначения, разного размера.

Магазин мер отличается от набора только тем, что он выполнен в одном едином устройстве.

Измерительный прибор — это средство измерений предназначенное для получения значений измеряемой физической величины в установленном диапозоне. По способу индикации, измерительные приборы делятся на показывающие и регистрирующие, хотя часто регистрирующие приборы являются показывающими.

Измерительный преобразователь служит для преобразования одной величины в другую. Он изменяет одну величину на другую в момент измерения.

По характеру преобразования различают аналбоговые; зифро — аналоговые; аналого — цифровые.

По расположению в измерительной цепи различают первичные и промежуточные.

Бывают передающие и масштабные преобразователи. Передающие служат для передкчи информации. Масштабные преобразователи меняют масштаб сигнала (пропроционально увеличивают или уменьшают).

Принципы, методы и методики измерений.

Принцип измерений — это физическое явление или эффект положенное в основу измерений. Допустим, для измерения температуры используются термо — электрические явления.

Метод измерения — это приём или совокуность приёмов сравнения измеряемой физической величины с её идиницей в соответствии с приципом измерений. Метод непосредственной оценки, метод сравнения с мерой, метод измерения замещением.

Методика — это установленная совокупность правил и операций при измерении, и их выполнение обеспечивает получение результатов с заданной точностью.4Условия измерений . Нормальные условия измерений - это условия измерений, которые характеризуются определённым набором фиизческих величин, при которых пренебрегают изменением результата измеренийю

Вводят понятие нормальное зщначение влияющей величины — то численное значение, которое пойдёт в нормальные увлвия измерений. Обычно погрешность, которая пишется на приборах и в методах, это погршеноть при нормальных условиях, в других условиях погрешность может отлдичаться.

Нормальная область значений влияющей величины — это область значений влияющей величины, при которойпроводится измерение.

Так же под нормальной областью значений имеют в виду, на сколько может отклоняться величина, которую измеряют. t0 = 20 гр. цельс. 0,05 гр. цельс. 19,95 — 20,05.

Погрешность измерений.

Погрешность результата измерений — отклонение результата измерения от истинного или действительного значения.

Абсолютная погрешность — это погрешность вырженная в единицах измеряемой величины.

Абсолютное значение погрешности — это значение погрешности без учёта её знака или модуль погрешности.

Для средств измерений погрешность дельта = А - Аи, тоесть разность между абсолютным значением истинным значением величины.

Если истинное значение величины не известно, тогда вместо него используют действительное значение.

Дельта = А — Аd

S = дельта/А * 100%.

относительная погрешность - это отношение абсолютной погрешности к результатом измерений или к действительному или истинному значению.

Приведённая погрешность — этоотношение абсолютной погршености к условно — принятому значению величины.

Sприв = дельта/Анорм * 100%.

Класс точности — это обобщённая характеристика определяемая пределами допускаемых основной и дополнительной погрешности, а так же другими средствами измерений, их свойствами влияющими на их точность. Правила обозначения классов точности определяются стандартами. Одним из распространённых вариантов является обозначение числом совпадающим с допускаемой основной приведённой погрешностью.

КТ = дельтаmax/Анорм * 100%, где дельтаmax — максимальная основная допускаемая приведённая погрешность.

Класс точности показывает, в каких пределах находится погрешность, но не является показателем точности измерения.

Вариация — это модуль разности показаний в одной и той же точке, при плавном подходе к этой точке со стороны меньших и больших значений.

Вариация может возникать из за сухого трения, явлений гистерезиса, механических погрешностей.

Так же как и погрешность вариацию часто выражают в процентах.

в прив = в/Априв * 100%.

Промах — это погрешность результата отдельного измерения, который резко отличается от остальных результатов. Иногда вместо промах вводят понятие грубая погрешность измерения.

Классификация погрешностей.

1. В зависимости от характера изменения величины во времени. Определяется по времеи.

1. Статические. Статическая погрешность - это погрешность измеряемой величины принимаемая за неизменную на протяжении времени измерения. При этом предполагается, что все переходные процессы завершены.

2. Динамичекие. Динамическая погрешность — это погрешность при измерении меняющейся велпчины.

2. В зависимости от условий измерения.

1. Основные. Основная погрешность — это погрешность при нормальных условиях(для данного инструмента)

2. Дополнительные. Дполнительная погрешность — это погрешность в следствии отклонения какой либо из влияющих величин.

Государственная система обеспечения единства измерний (ГСИ).

Государственная система обеспечения единства измерений — это комплекс нормативных документов различных уровней, устанавливающих правила, нормы, требования направленны на доситжение единства измерений в стране.

Обеспечение единства измерений — это деяетельность метрологических служб направленных на достижение и поддержание единства измерений.

Единство измерений — это состояние измерений, когда их результаты выражаются в узаконеных единицах, размеры которых равны эталонным, а погрешности известны и с заданной вероятностью не выходят за установленные пределы.

Поверка — это установление органом государственной метрологической службы пригодности средст измерений к применению на основании экспериментально определяемых метрологических характеристик, и подтверждения их соответсвия обязательным требованиям.

Измерительные преобразователи.

Преобразования в измерительных преобразователях основаны на физических или физико — химических явлениях, определяющих зависимость между входным и выходным сигналом. По принципу действия делятся на:

• ёмкостные;

• пьезоэлектрические;

• тензорезистивные;

• потенциометрические;

• термисторыные;

• основанные на эффектах Холла, кориолиса и других.

По виду энергии делятся на:

• механические;

• электрические;

• магнитные;

• энергии излучения;

• химической энергии.

По их практическому применению на пример для измерения давления; температуры; расхода.

Измерительные преобразователи — это основные элементы всех систем управления. Они определяют качество и стоимость управляющих систем.

Устройства систем управления:

• измерительные преобразователи 40%;

• устройства обработки данных 20%;

• устройства регистрации и отображения данных 40%.

Современных этап развития измерительной техники характеризуется разработкой многофункциональных интиллектуальных датчиков, которые обеспечивают высокую точность, надёжность и длительный срок службы.

Схема измерительного преобразователя.

Схема измерительной системы.

Промежуточные преобразователи.

Промежуточным преобразователем называют элемент занимающий в измерительной цепи место после первичного преобразователя. Основное назначение — это преобразование входящего сигнала в форму удобную для последующего преобразования и передачи.

Классификация преобразующих устройств.