2.6. Методика решения формализуемых задач принятия решений

2.6.1. Обзор математических методов решения задач оптимизации

Формализуемые решения принимаются на основе математических методов по соответствующим алгорит­мам. Принятие формализованного решения требует на­личия следующих составных частей:

• математической модели объекта или процесса уп­равления;

• информации, необходимой для решения задачи;

• алгоритма решения задачи, как правило, на ком­пьютере.

Математическая модель задачи-оптимизации фор­мализуемого решения включает следующие элементы:

• целевую функцию (критерий управления)

• Ф = F(x_j) → max (min, const),

• где x_j - искомые переменные;

• ограничения, устанавливающие зависимости меж­ду текущими переменными:

g_j ( x_.j ) ≤ a_i , k_i ( x_j ) ≤ b_i ;

• граничные условия, показывающие, в каких пре­делах могут быть значения искомых переменных в оптимальном решении:

d_j ≤ x_j ≤ D_j

при i = 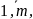j =

Непременным требованием для решения задачи оп­тимизации является условие п > т.

Математическая модель является эффективным средством получения ответов на широкий круг вопросов, возникающих при принятии решения. Она должна учи­тывать основные свойства моделируемого объекта (про­цесса) и пренебрегать его второстепенными свойствами.

Исходная информация для принятия решения дол­жна отвечать требованиям, перечисленным в 1.2.

В зависимости от критерия эффективности, страте­гий и факторов управления (см. 1.1) выбирается алго­ритм оптимизации решения задачи, базирующийся на каком-то математическом методе. Перечислим основные методы оптимизации:

• линейное и динамическое программирование (за­дачи распределения ресурсов);

• теория массового обслуживания (задачи со слу­чайным характером поступления и обслуживания заявок в системе);

• имитационное моделирование (задачи, где реаль­ный эксперимент заменяется имитационной моде­лью);

• статистическое моделирование (задачи, в которых результат находится методами математической статистики из большого числа расчетов с различ­ными факторами);

• теория управляемых марковских процессов (задачи со случайными неконтролируемыми факторами);

• теория игр (состязательные задачи в условиях неопределенности);

• теория расписаний (задачи календарного упоря­дочения работ);

• сетевое планирование и управление (задачи с не­определенной оценкой времени выполнения раз­личных видов работ);

• векторная оптимизация (многокритериальные за­дачи);

• теория распознавания образов (задачи поиска) и другие методы.

Последовательность работ при принятии оптималь­ного формализуемого решения можно разделить на сле­дующие этапы:

• содержательная постановка задачи (детерминиро­ванные или случайные исходные данные; непре­рывные, целочисленные или дискретные искомые переменные; пределы, в которых могут быть зна­чения искомых переменных; линейные или нели­нейные зависимости между переменными; целе­вая функция управления);

• построение математической модели оптимизации решения задачи;

• сбор исходной информации (чтобы не обрабаты­вать избыточную информацию, этот этап делает­ся после формулировки математической модели);

• решение задачи, которое во многих случаях мо­жет иметь много вариантов;

• анализ предложенных решений;

• принятие оптимального решения (нужно по­мнить, что решение принимает руководитель, а ПЭВМ только рекомендует ему варианты реше­ния);

• графическое представление результатов решения и анализа, являющееся серьезным фактором при принятии решения.

Перечисленные задачи могут быть решены только с помощью ПЭВМ.