
Вопрос 30
понятие о цифровой модели местности
Цифровая модель местности (ЦММ) представляет собой совокупность данных (плановых координат и высот) о множестве её точек. Указанная совокупность может представлять собой отдельно цифровую модель рельефа (ЦМР) и цифровую модель контуров (ЦМК), т.е. ситуации местности. В последнем случае элементы ситуации могут быть заданы только плановыми координатами Х и Y. Цифровая модель рельефа обязательно задаётся одновременно плановыми координатами и высотами Н.
Цифровая информация о местности очень удобна для представления и хранения в электронном виде.
ЦММ эффективно пользоваться при аналитических проектных работах. В этом случае такие модели строят с помощью топографических карт. Очевидно, что при построении дискретной картины местности (количество точек ограничено) криволинейные контуры необходимо заменять отрезками ломаных линий. При этом отклонение криволинейного контура от сглаживающей ломаной линии не должно быть больше 0,3 мм. Точки контуров (углы зданий, углы поворота линейных объектов и т.п.) определяют их координатами, измеренными непосредственно по карте, либо используют их значения, полученные в процессе топографической съёмки.
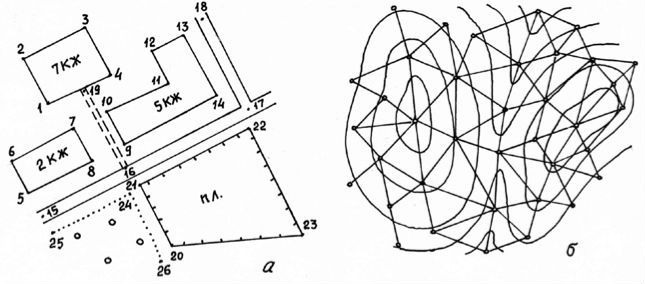 Цифровая
модель местности: а) представление
ситуации; б) представление рельефа.
Цифровая
модель местности: а) представление
ситуации; б) представление рельефа.
Аналитическая форма представления ситуации (рис. 8.1 а) имеет вид таблицы с номерами точек (1 – 26), их координатами Х, У и указанием взаимосвязи точек контура, например, 1-2-3-4 – сплошной контур дома, 25- 24-26 – контур леса. Такая информация записывается в кодированном виде в таблице.
При задании рельефа в аналитической форме используют два метода. В первом, в зависимости от сложности рельефа, координаты и высоты точек определяют в узловых точках сплошной равномерной сети равносторонних треугольников и квадратов. В каких-то местах эта сеть может быть гуще, в других – реже. Такой метод имеет недостаток, определяемый рассогласованностью выбора координируемой точки с характером рельефа местности. Во втором методе (рис. 7.1 б) выбор координируемых точек определяется особенностями рельефа в тех или других частях местности. Точки выбирают на характерных линиях (линиях водослива и водораздела), на вершинах возвышенностей и по дну котловин (ям), в седловинах, в местах перегибов рельефа с выделением фрагментов с однородным склоном и т.п. Таким образом, во втором методе используется подход, соответствующий методике топографической съёмки рельефа, например, при тахеометрической съёмке.
Вопрос 31
задачи решаемые на топографических картах с горизонталями перечень задач
Определение отметок точек местности по горизонталям
а) Точка лежит на горизонтали. В этом случае отметка точки равна отметке горизонтали (см. рис. 35): HА = 75 м; НС = 55 м.
б) Точка лежит на скате между горизонталями. Если точка лежит между горизонталями, то через нее проводят кратчайшее заложение, масштабной линейкой измеряют длину отрезков а и b (см. рис. 35, точка В) и подставляют в выражение

где h – высота сечения рельефа. Если точка лежит между горизонталью и полугоризонталью, то вместо h в формулу подставляют 0,5h.
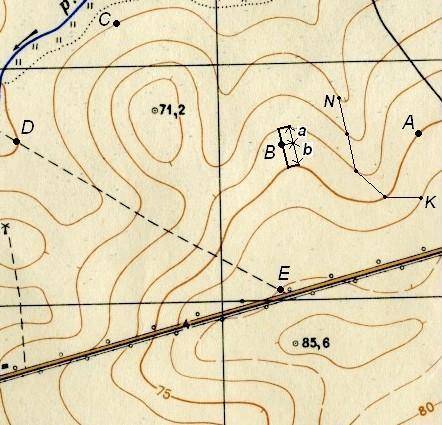
Рис. 35. Решение задач на карте с горизонталями
3.5.2. Определение крутизны ската
Крутизна ската по направлению заложения определяется двумя показателями – уклоном и углом наклона по формуле

Следовательно, тангенс угла наклона линии к горизонту называется её уклоном. Уклон выражают в тысячных – промиллях (‰) или в процентах (%). Например: i = 0,020 = 20‰ = 2%.
Для графического определения углов наклона по заданному значению заложения d, масштабу М и высоте сечения рельефа h строят график заложений (см. рис. 36).
Вдоль прямой линии основания графика намечают точки, соответствующие значениям углов наклона. От этих точек перпендикулярно к основанию графика откладывают в масштабе карты отрезки, равные соответствующим заложениям, а именно
![]()
Концы этих отрезков соединяют плавной кривой (см. рис. 36).
Заложение линии, угол наклона которой надо определить, снимают с карты при помощи измерителя, а затем, укладывая на графике между основанием и кривой измеренный отрезок, находят соответствующее ему значение угла наклона.
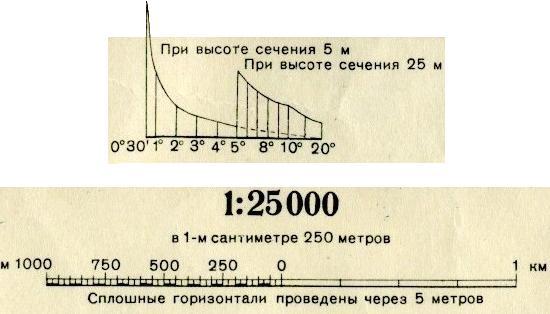
Рис. 36. График заложений для углов наклона
Аналогично строят и пользуются графиком заложений для уклонов (рис. 37).

Рис. 37. График заложений для уклонов
3.5.3. Построение линии с заданным уклоном
Задача построения линии с заданным уклоном решается в проектировании трасс железных, автомобильных и других линейных сооружений. Она заключается в том, что из некоторой точки, обозначенной на карте, необходимо провести линию с заданным уклоном i по заданному направлению. Для этого сначала определяют значение заложения d, соответствующее заданным i и h. Его находят по графику заложения уклонов или вычисляют по формуле
d = h/i .
Далее, установив раствор измерителя равным полученному значению d, ставят одну его ножку в начальную точку K, а другой засекают ближайшую горизонталь и тем намечают точку трассы, из которой в свою очередь засекают следующую горизонталь, и т.д. (см. рис. 38).

Рис. 38. Построение линии с заданным уклоном
3.5.4. Построение профиля по топографической карте
Профилем местности называют уменьшенное изображение вертикального разреза местности по заданному направлению.
Пусть требуется построить профиль местности по линии DE, указанной на карте (рис. 39). Для построения профиля на листе бумаги (как правило, используется миллиметровая бумага) проводят горизонтальную прямую и на ней, обычно в масштабе карты (плана), откладывают линию DE и точки её пересечения с горизонталями и полугоризонталями. Далее из этих точек по перпендикулярам откладывают отметки соответствующих горизонталей (на рис. 39 это отметки 50, 55, 60, 65, 70, 75, 80 и 82,5 м). Чтобы отобразить профиль более рельефно, отметки точек обычно откладывают в масштабе в 10 раз крупнее масштаба плана. Соединив прямыми концы перпендикуляров, получают профиль по линии DE.

