V1: Гармонический анализ
V2: Графики периодических функций
I: {{1.1}} И; K=А
S: Укажите график периодической функции
-:
-:
+:
-:
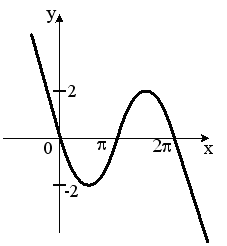
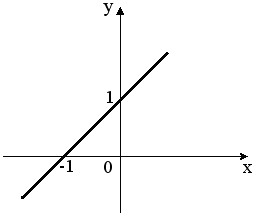
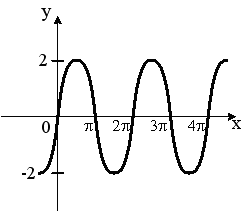
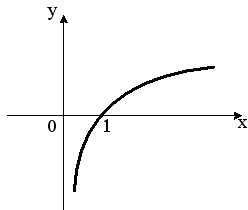
I: {{1.2}} И; K=А
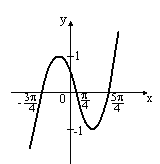
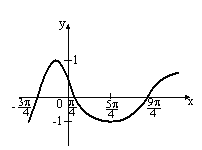
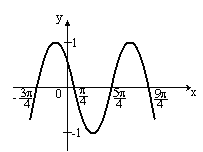
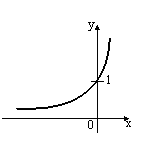
S: Укажите график периодической функции
-:
-:
+:
-:
I: {{1.3}} И; K=А
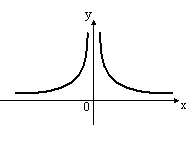
S: Укажите график периодической функции
-:
-:
+:
-:
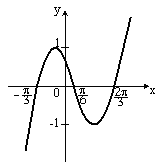
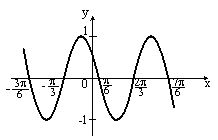
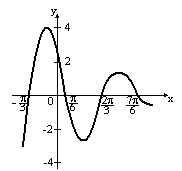
I: {{1.4}} И; K=А
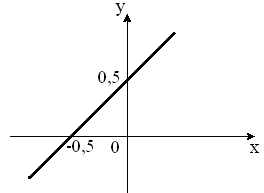
S: Укажите график периодической функции
-:
-:
+:
-:
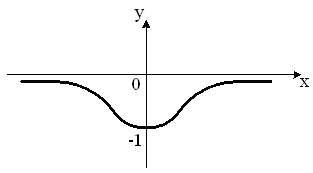
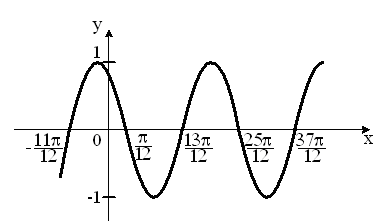
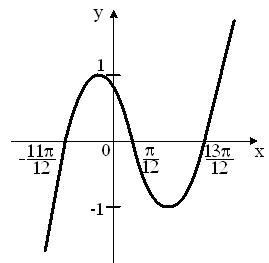
I: {{1.5}} И; K=А
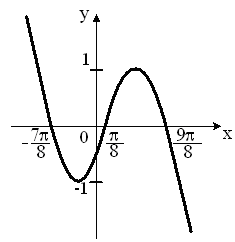
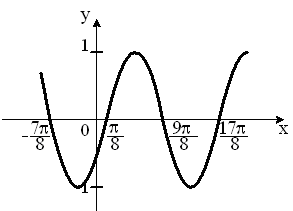
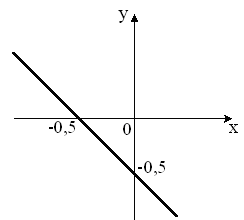
S: Укажите график периодической функции
-:
-:
+:
-:
I: {{1.6}} И; K=B
S:
На рисунке изображен график периодической
функции
.
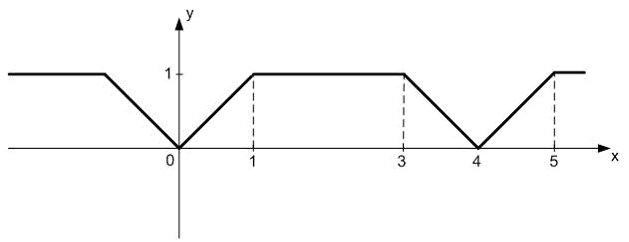
Ее аналитическое
представление на отрезке
имеет вид
-:
-:
+:
-:
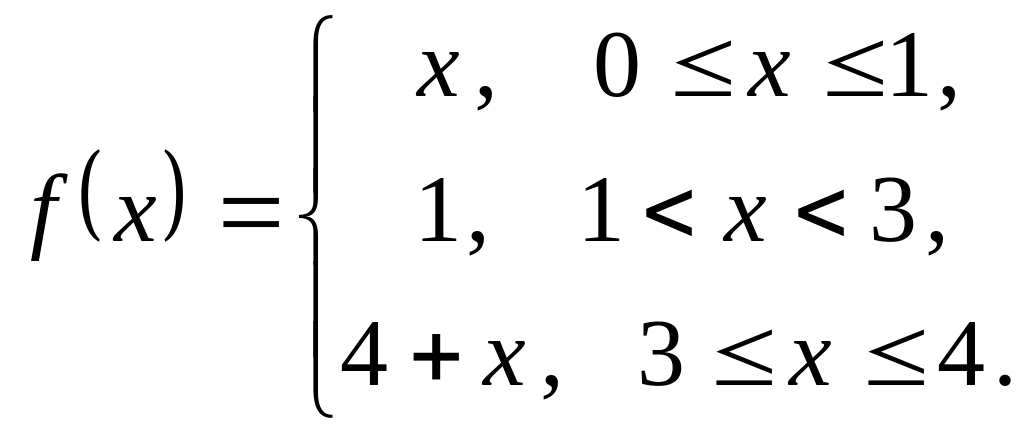
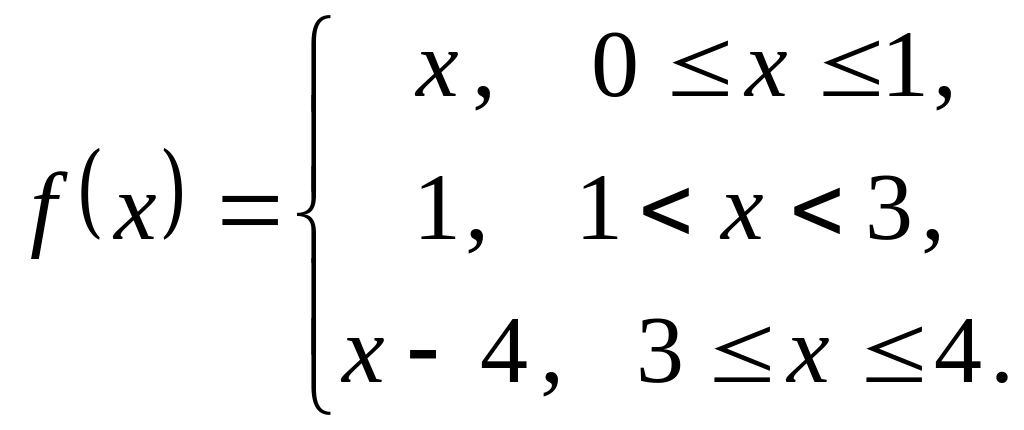
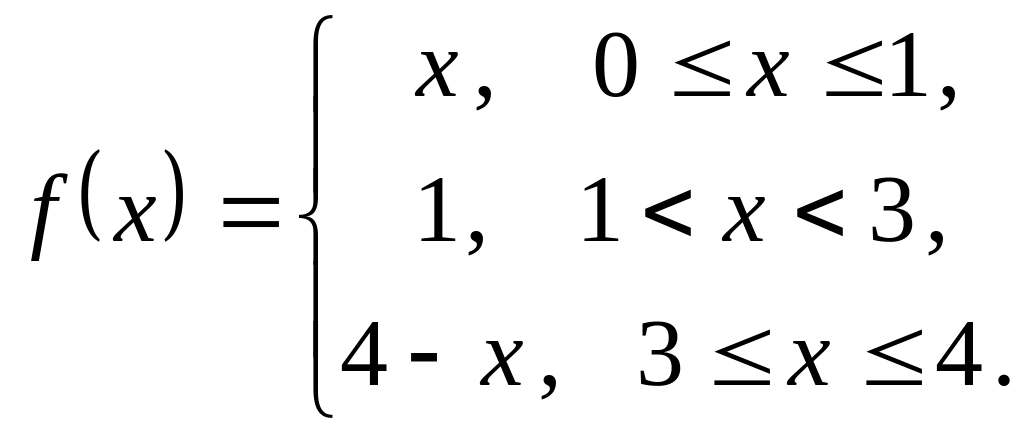
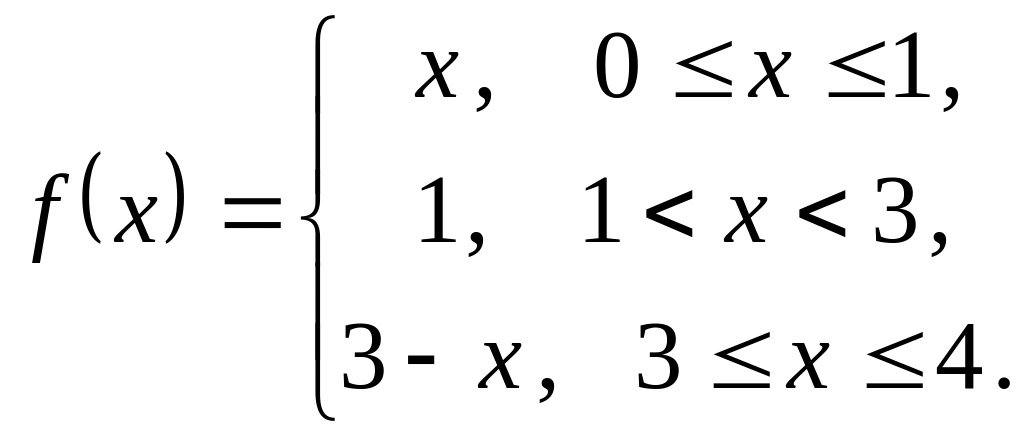
I: {{1.7}} И; K=B
S:
На рисунке изображен график периодической
функции
,
,
с ее периодическим продолжением.
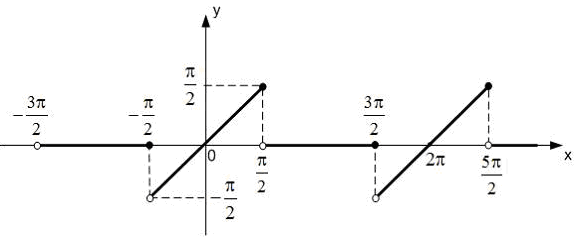
Какое из следующих
утверждений справедливо для периодического
продолжения функции
?
-: периодическое
продолжение с периодом
функции
является непрерывным
-: периодическое
продолжение с периодом
функции
имеет точки разрыва второго рода
+: периодическое продолжение с периодом функции имеет точки разрыва первого рода
-: периодическое продолжение с периодом функции является непрерывным
I: {{1.8}} И; K=B
S: На рисунке изображен график периодической функции .
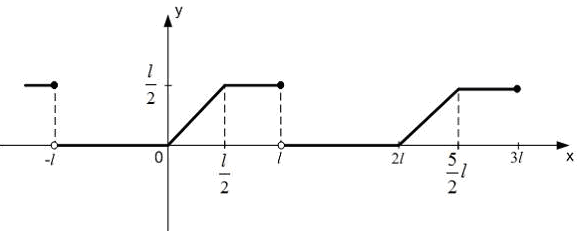
Ее аналитическое
представление на промежутке
имеет вид
-:
-:
+:
-:
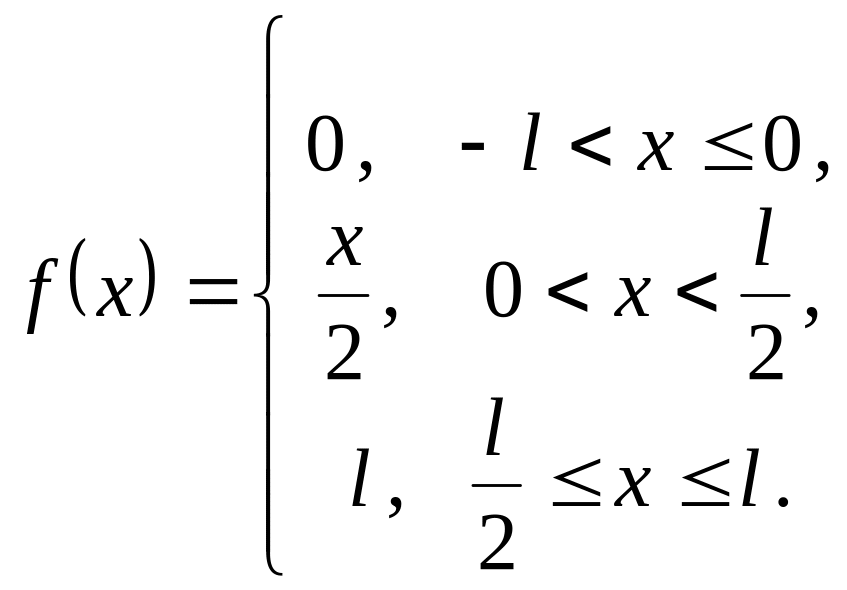
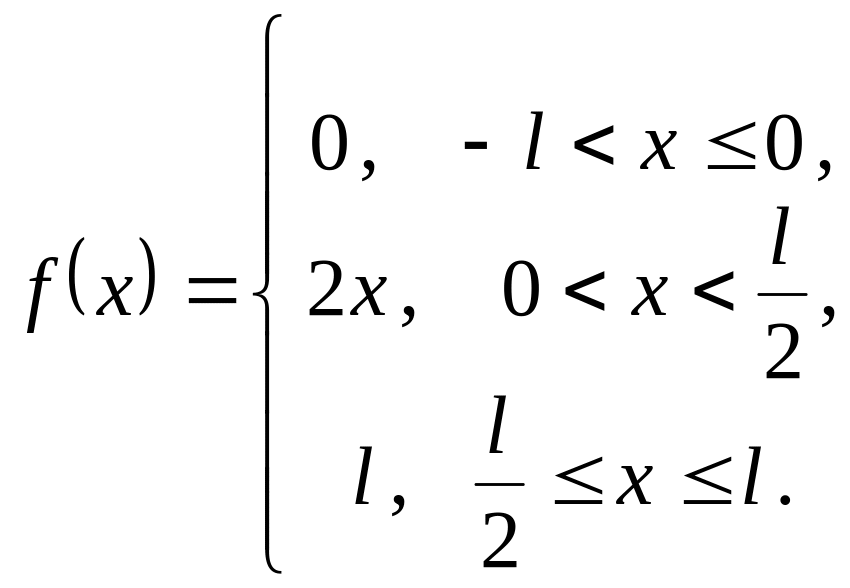
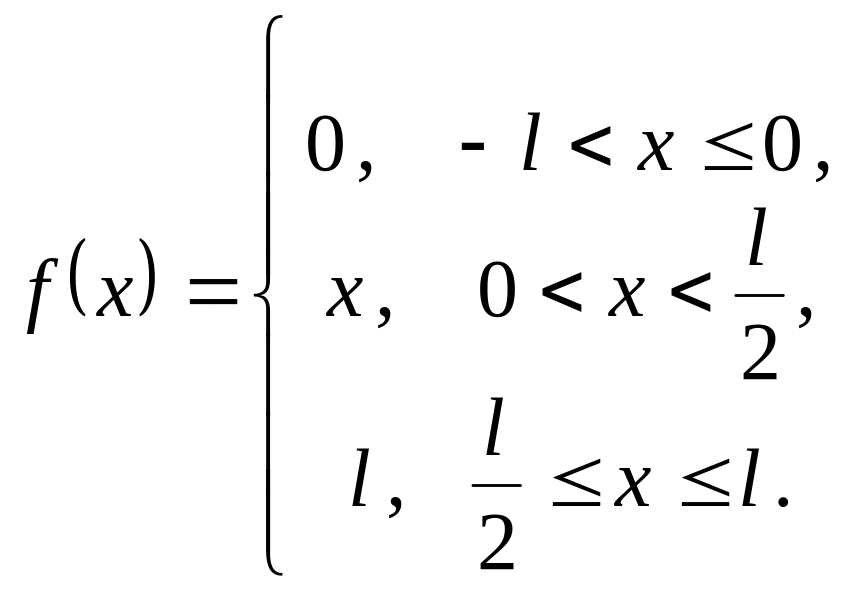
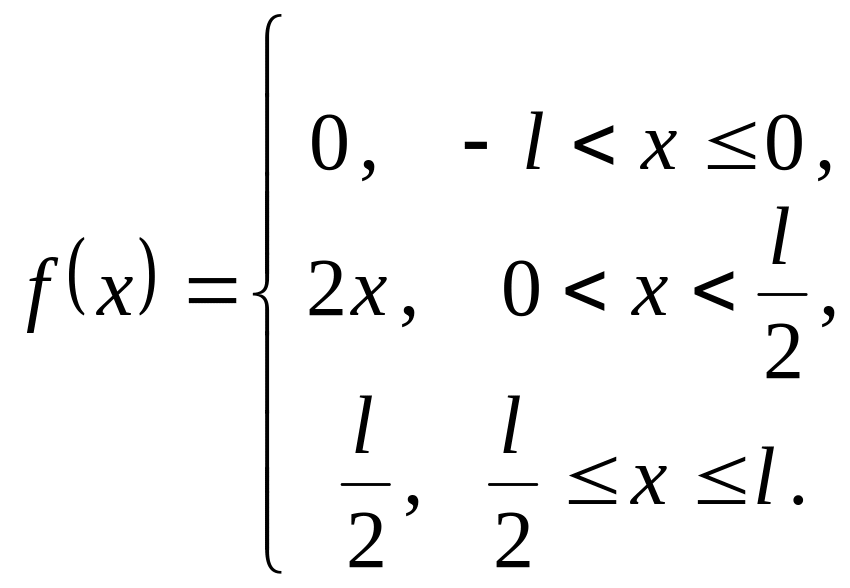
I: {{1.9}} И; K=B
S:
На рисунке изображен график функции
,
,
с ее периодическим продолжением.
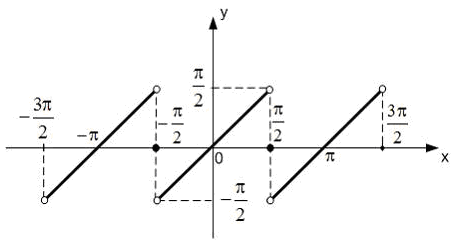
Периодическое продолжение на числовую прямую является…
-: четной функцией
с наименьшим периодом
-: четной функцией с наименьшим периодом
+: нечетной функцией с наименьшим периодом
-: нечетной функцией с наименьшим периодом
I: {{1.10}} И; K=B
S:
На рисунке изображен график функции
,
,
с ее периодическим продолжением.
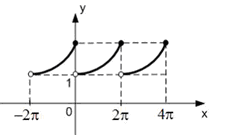
Периодическое продолжение на числовую прямую является…
-: четным продолжением
-: невозможным
+: периодическим продолжением общего вида
-: нечетным продолжением
I: {{1.11}} И; K=B
S: На рисунке изображен график функции , , с ее периодическим продолжением.
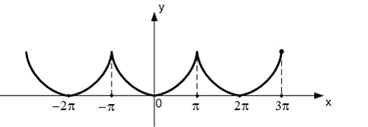
Периодическое продолжение на числовую прямую является…
-: нечетной функцией с наименьшим периодом
-: четной функцией с наименьшим периодом
+: четной функцией с наименьшим периодом
-: нечетной функцией с наименьшим периодом
V2: Период функции
I: {{2.1}} И; K=B
S: Установите соответствие между периодической функцией и значением ее периода
L1:
L2:
L3:
R1: 4
R2:
R3: 5
R4: 2
R5:
I: {{2.2}} И; K=B
S:
Произведение значений параметра а,
при которых период функции
равен
,
равно …
-:
-: 32
+: 384
-: 2
I: {{2.3}} И; K=B
S:
Произведение значений параметра а,
при которых период функции
равен
,
равно …
-: 3
-: 1
+:
-:
I: {{2.4}} И; K=А
S:
Для периодической функции
с периодом
при всех х
из области
определения выполняется равенство …
-:
-:
+:
-:
I: {{2.5}} И; K=А
S:
Функция
– четная, имеет период 10 и на отрезке
задана в виде
,
тогда
равно …
-: 12
-: 15
+: 16
-: 0
I: {{2.6}} И; K=B
S:
Произведение значений параметра а,
при которых период функции
равен
,
равно …
-:
-:
+: 2,25
-: 0,5
I: {{2.7}} И; K=B
S:
Сколько функций их указанных:
,
имеют наименьший период, равный
?
-: 1
-: 3
+: 2
-: 4
I: {{2.8}} И; K=А
S: Периодической является функция
-:
-:
+:
-:
I: {{2.9}} И; K=А
S: Периодической является функция
-:
-:
+:
-:
I: {{2.10}} И; K=А
S:
Для периодической функции
с периодом
при всех х
из области
определения выполняется равенство …
-:
-:
+:
-:
