Свойства определенного интеграла. Вычисление определенного интеграла. Свойства определенного интеграла
Справедливы следующие свойства определенного интеграла.
1. 
dx =
0, 
=
0.
2. 
=
- 
.
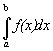3. Если функция y=f(x) интегрируема по большему из промежутков [a,b], [a,с], [с,b], то она интегрируема по двум другим промежуткам, причем выполняется равенство
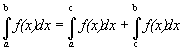
независимо от расположения точек а, b, c
рис
22
Доказательство. 1) Случай acb. Возьмем произвольное разбиение отрезка [a,b]:
x0 = a x1 x2 ... с … xn = b.
Очевидно, что для интегральных сумм будет выполняться следующее равенство:
.
Переходя к пределу при измельчении длин отрезков разбиения, получим требуемое равенство.
2) Случай саb. Согласно случаю 1
.
Используя свойство 2, получим
,
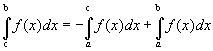отсюда
.
Аналогично рассматриваются остальные случаи.
4. Постоянный множитель можно выносить за знак определенного интеграла.
.
.
5. Если функции f(x) и g(x) интегрируемы по отрезку [a,b], то и их алгебраическая сумма также интегрируема по [a,b], причем интеграл от алгебраической суммы равен алгебраической сумме интегралов.
.
Это равенство непосредственно следует из равенства для интегральных сумм.
.
6. Пусть функция y = f(x) определена на отрезке [a,b]. Рассмотрим функцию
Ф(х)
= 
.
В каждой точке непрерывности функции f(x) функция Ф(х) имеет производную, которая равна f(x).
рис
23
Ф’(х) = f(x), т. е. Ф(х) является первообразной для функции f(x).
Вычисление определенного интеграла
Пусть
функция y
= f(x) непрерывна на
[a,b],
тогда функция 
будет
являться первообразной.
Пусть F(x) -
любая первообразная функции f(x).
Тогда по свойству первообразных Ф(х)
= F(x) + С. Найдем С.
.
Следовательно, Ф(х) = F(x) - F(a).
Найдем Ф(b):
,
Ф(b) = F(b) - F(a).
Из двух последних равенств следует, что
–
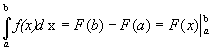формула
Ньютона – Лейбница.
С помощью этой формулы вычисляется определенный интеграл, если известна любая первообразная подынтегральной функции.
Интегрирование по частям и метод замены переменной в определенном интеграле.
1. Пусть
функции u(x) и 
(x) имеют непрерывные производные на
отрезке [a,b].
Проинтегрируем равенство
для дифференциалов 
по
отрезку [a,b].
,
,
,
- формула интегрирования по частям в определенном интеграле. Эта формула применяется к тем же типам интегралов, которые были рассмотрены в неопределенном интеграле.
2. Пусть y =f(x) непрерывна на отрезке [a,b] и на этом отрезке она имеет первообразную F(x).
.
Пусть
функция y
= 
(t)
является дифференцируемой
функцией на [
] и
ее производная непрерывна на [
]. Она
переводит отрезок [
] в [a,b].
: [
] [a,b].
() = a, () = b (концы переводит в концы).
Тогда справедлива формула замены переменной в определенном интеграле:
.
Доказательство. 
,
.
Пример
1. 
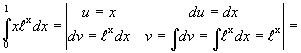
Пример
2. 
=
=
.
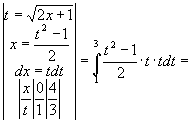
Приложения определенного интеграла.
1. Вычисление площадей фигур, расположенных под (над) графиком функции на некотором отрезке. Это приложение вытекает из геометрического смыслаопределенного интеграла.
S = .
y=f(x) рис 24
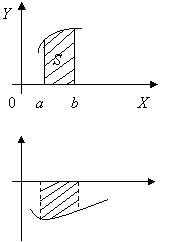рис25
S = 
.
2. Вычисление площади фигур, ограниченных графиками двух функций на некотором отрезке.
S
=S2-S1=
=
, где S1 и S2 -
площади криволинейных трапе ций
под графиками функций y=f1(x) и y=f2(x).
Пример. y=x2-1, y=x2- 1
y=x+1 
рис26
Найдем абсциссы
точек пересечения.
x2 –1 = x+1,
x2 – x – 2 =0,
x1 =2 x2 = -1.
.
=
.
3. Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОX.
Рис 27
.
Пример. y=sinx, x[0,].
рис
28
.
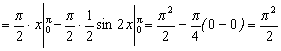4. Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОY.
|
|
|
|
Рис
29
, где x
= f -1 (y) -
обратная функция к функции y
= f(x).
Пример. y = 
, y[1,4].
рис30
.
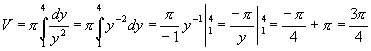