Замена переменных в двойном интеграле

Пусть функция непрерывна в замкнутой области , тогда существует двойной интеграл . Если область связана с областью в плоскости формулами (10) и выполняются условия п. , то справедлива формула замены переменных в двойном интеграле:

. (12)

Производить в двойном интеграле замену переменных по формуле (12) целесообразно лишь в том случае, когда область интегрирования G значительно проще области .

В частном случае перехода к полярным координатам (11) имеем , , , и формула (12) приобретает вид

. (13)

К полярным координатам целесообразно переходить, например, когда область есть круг с центром в начале координат или часть такого круга. При этом, как правило, в повторном интеграле в качестве внешней переменной берётся угол .

П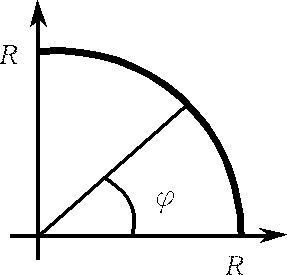 ример 3. Перейдём в интеграле

к полярным координатам. Сначала восстановим область интегрирования – это часть круга радиуса с центром , лежащая в первом квадранте (рисунок ). Совместим полярную систему координат с прямоугольной. Мысленно вращая радиус-вектор в положительном направлении (против часовой стрелки), определяем, что в точках области . «Выпуская» из полюса луч в указанном растворе угла , получаем, что луч входит в область при и выходит из неё через дугу окружности , уравнение которой в полярных координатах имеет вид . Таким образом, в полярных координатах область интегрирования описывается системой неравенств . Следовательно, после замены переменных интеграл приобретает вид

.

Некоторые приложения двойного интеграла

1. Вычисление объёма цилиндрического тела.

В соответствии с геометрическим смыслом двойного интеграла объём цилиндрического тела, ограниченного сверху поверхностью , снизу – областью D плоскости Oxy, с боков – цилиндрической поверхностью с образующими, параллельными оси , определяется по формуле (4).

Пример 4. Найти объём части кругового цилиндра , ограниченной плоскостями , , , верхней половиной конуса и располагающейся в первом октанте .

Данное тело является цилиндрическим. Его образующие параллельны оси , основанием является область плоскости , изображённая на рисунке . Сверху тело ограничено поверхностью . По формуле (4) объём тела равен . Поскольку область есть часть круга с центром в начале координат, перейдём к полярным координатам и используем решение примера 3:

(куб.ед.).

В общем случае, когда цилиндрическое тело ограничено снизу поверхностью , такой что при , где – проекция тела на плоскость Oxy, объём тела равен

. (14)

2. Вычисление площади плоской фигуры.

Согласно свойству 4 двойного интеграла площадь области плоскости Oxy выражается формулой .

Пример 5. Найдём площадь фигуры , ограниченной линиями , , . Опишем область системой неравенств, для чего определим точки пересечения линий: . Из рисунка следует, что . Имеем тогда: (кв.ед.).

3. Вычисление площади поверхности.

Пусть в пространстве задана гладкая поверхность , определяемая уравнением . Если поверхность однозначно проектируется на область плоскости Oxy, то площадь поверхности находится по формуле

. (15)

Пример 6. Вычислим площадь части поверхности параболоида вращения , ограниченной цилиндром . Проекцией поверхности на плоскость является область . Имеем , . По формуле (15) площадь поверхности равна . Переходя к полярным координатам, получаем: = (кв.ед.).

4. Вычисление массы тонкой пластинки.

Пусть на плоской области распределено некоторое вещество. Выделим в произвольную часть площадью . Пусть масса вещества, приходящаяся на , составляет . Отношение называется средней поверхностной плотностью вещества в области . Будем теперь уменьшать область , стягивая её в точку ; площадь при этом будет стремиться к нулю. Если существует предел , то он называется поверхностной плотностью вещества в точке М и является функцией этой точки:

. (16)

Тонкую пластинку мы можем рассматривать как массу, непрерывно распределённую с поверхностной плотностью по плоской области . Разобьём область на части с площадями соответственно, столь малые, что плотность в каждой части будем считать постоянной и равной плотности в произвольно выбранной точке .

Тогда сумма приближённо выражает массу всей пластинки, причём тем точнее, чем меньше размеры частичных областей . Точное значение массы равно пределу этой суммы при и стремлении к нулю наибольшего из диаметров частичных областей . С другой стороны, этот предел равен двойному интегралу от функции по области . Получаем формулу вычисления массы тонкой пластинки: , или

, (17)

если область является частью плоскости .

5. Вычисление координат центра тяжести плоской фигуры.

Пусть плоская фигура занимает область в плоскости . Если по ней непрерывно распределена масса с поверхностной плотностью , то координаты центра тяжести плоской фигуры определяются по формулам

, , (18)

где – масса фигуры, вычисляемая по формуле (17), а выражения

, (19)

называются статическими моментами плоской фигуры относительно осей и соответственно.

60