2.3. Метод потенциалов

После того, как было найдено первоначальное распределение поставок, необходимо, для нахождения оптимального распределения поставок, применить метод потенциалов.

1 шаг. Нахождение потенциалов строк и столбцов.

Вычисляются потенциалы поставщиков и потребителей . Полагают, что потенциалы для заполненных ячеек распределительной таблицы удовлетворяют условию:

Число занятых клеток равно (m+n-1) и, следовательно, для определения потенциалов, надо решать систему из (m+n-1) уравнений с (m+n) неизвестными. Система является неопределенной, т. е. имеет бесконечное множество решений, поэтому для облегчения нахождения частного решения полагают . Далее двигаются по заполненным клеткам и находят остальные потенциалы.

2 шаг. Нахождение матрицы оценок.

Вычисляются матрица оценок с элементами, определяемыми следующим образом:

Если все элементы матрицы оценок неотрицательны, т. е.

то найденное распределение поставок будет оптимальным. Если для всех ячеек , то оптимальный распределение поставок является единственным. Если какая-либо оценка , то существует бесчисленное множество решений с одинаковым значением целевой функции.

Если какое-либо значение , то найденное распределение поставок не является оптимальным и необходимо строить так называемый цикл пересчета, в котором перераспределяются поставки.

3 шаг. Построение цикла пересчета.

Среди отрицательных элементов матрицы оценок выбираем наименьшее. Клетка (она, кстати, всегда будет свободной) с таким значением будет вершиной цикла пересчета.

Цикл пересчета представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся только под прямым углом. В одной строке (столбце) может быть только одно звено, соединяющее только две клетки.

В цикле всего одна свободная клетка, остальные заполненные. В цикле всегда четное число клеток. В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.

В клетках со знаком «–» находим наименьшую поставку, которую передаем по циклу. В клетки с «+» эту поставку прибавляем, с «–», соответственно, вычитаем. Если при этом сразу в нескольких клетках получается 0, то только в одной клетке ничего не пишем, т.е. считаем ее свободной, а в остальные обнулившиеся клетки записываем формально нулевую поставку.

Измененные значения клеток цикла пересчета ставим в распределительную таблицу и возвращаемся к шагу 1.

Пример. Найдем оптимальное распределение поставок для нашего примера. Вначале перепишем таблицу с первоначальным распределением поставок в виде:

	5 100	8 60	24	16
	7	12	9 60	5 250
	15	17 110	10 140	7

1 итерация.

1 шаг. Нахождение потенциалов строк и столбцов.

Определим потенциалы поставщиков и потребителей . Полагают, что потенциалы для заполненных ячеек распределительной таблицы удовлетворяют условию:

При этом полагают . Далее двигаются по заполненным клеткам и находят остальные потенциалы.

Двигаемся по первой строке распределительной таблицы. Заполненных клеток здесь две: (1,1) и (1,2). Вначале идем до клетки (1,1). Этой клетке соответствует потенциал первой строки (т. к. клетка находится в первой строке) и потенциал первого столбца (клетка находится в первом столбце). Должно выполняться равенство:

Мы потребовали, чтобы . Значение . Следовательно, значение . Записываем его в последней сроке распределительной таблицы.

В первой строке распределительной таблицы есть, как было указано выше, еще одна заполненная клетка. Это клетка (1,2). Этой клетке соответствует потенциал первой строки (т. к. клетка находится в первой строке) и потенциал второго столбца (клетка находится во втором столбце). Должно выполняться равенство:

Мы потребовали, чтобы . Значение . Следовательно, значение . Записываем его в последней сроке распределительной таблицы.

Больше никакой информации из первой строки мы не можем почерпнуть, т. к. в ней нет больше заполненных клеток. Поэтому рассматриваем столбцы, для которых мы нашли потенциалы. Это первый и второй столбцы.

Смотрим на первый столбец. В нем только одна заполненная клетка, и мы ее уже использовали для нахождения потенциала первого столбца.

Смотрим на второй столбец. В нем, кроме уже использованной заполненной клетки в первой строке, есть еще одна заполненная клетка в третьей строке, а именно клетка (3,2). Этой клетке соответствует потенциал третьей строки (т. к. клетка находится в третьей строке) и потенциал второго столбца (клетка находится во втором столбце). Должно выполняться равенство:

Мы нашли, что . Значение . Следовательно, значение . Записываем его в последнем столбце распределительной таблицы.

Больше заполненных клеток в столбце 2 нет, и мы не можем больше почерпнуть информацию из него.

Но мы теперь знаем потенциал еще одной строки. Это строка 3. В этой строке есть две заполненные клетки. Одну мы уже использовали для нахождения потенциала третьей строки. Рассмотрим другую заполненную клетку в третьей строке, а именно клетку (3,3). Этой клетке соответствует потенциал третьей строки и потенциал третьего столбца . Должно выполняться равенство:

Мы нашли, что . Значение . Следовательно, значение . Записываем его в последней строке распределительной таблицы.

Далее смотрим на третий столбец. В нем есть заполненная клетка (2,3). Совершая действия, аналогичные выше рассмотренным, находим, что потенциал второй строки равен 8, а потенциал четвертого столбца равен –3. В результате получили следующую таблицу:

	5 100	8 60	24	16
	7	12	9 60	5 250
	15	17 110	10 140	7

2 шаг. Нахождение матрицы оценок.

Вычисляются матрица оценок с элементами, определяемыми следующим образом:

Получаем матрицу оценок:

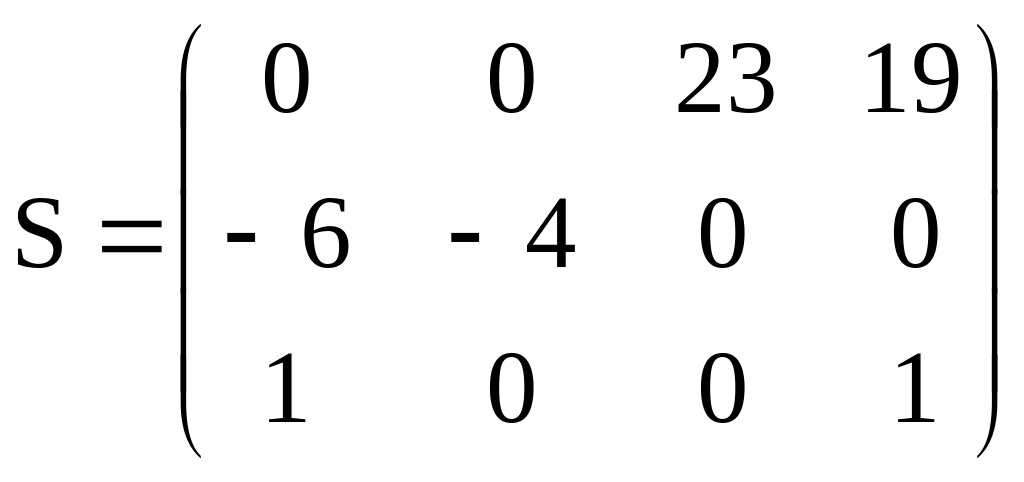
3 шаг. Построение цикла пересчета.

Среди отрицательных элементов матрицы оценок выбираем наименьшее. В нашем случае это –6, которое находится в клетке (2,1). Эта свободная клетка будет вершиной цикла пересчета. Цикл пересчета, как было указано выше, представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся только под прямым углом. В одной строке (столбце) может быть только одно звено, соединяющее только две клетки.

В цикле всего одна свободная клетка, остальные заполненные.

Мы двигаемся из клетки (2,1). Далее идем только по заполненным клеткам так, чтобы вернуться назад, и при этом учитываем все вышеперечисленные правила. Поэтому получаем следующий путь:

В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.

Из клеток со знаком «–» находим наименьшую поставку. У нас три клетки со знаком «–». Это клетки (1,1), (2,3) и (3,2). Наименьшая поставка находится в клетке (2,3) и она равна 60. Эту поставку передаем по циклу. В клетки с «+» ее прибавляем, с «–», соответственно, вычитаем. Например, клетка (3,3) со знаком «+», старая поставка в ней равнялась 140, прибавляем к ней 60, получаем 200. Клетка (3,2) была со знаком «–» и старая поставка в ней равнялась 110. Отнимаем 60 и получаем, что новая поставка в этой клетке равна 50. Свободная клетка (2,1) становится заполненной клеткой с поставкой 60, а ранее заполненная клетка (2,3) становится заполненной. Окончательно получаем новую распределительную таблицу:

	5 40	8 120	24	16
	7 60	12	9	5 250
	15	17 50	10 200	7

2 итерация.

1 шаг. Нахождение потенциалов строк и столбцов.

Находим потенциалы строк и столбцов.

2 шаг. Нахождение матрицы оценок.

Получаем матрицу оценок:

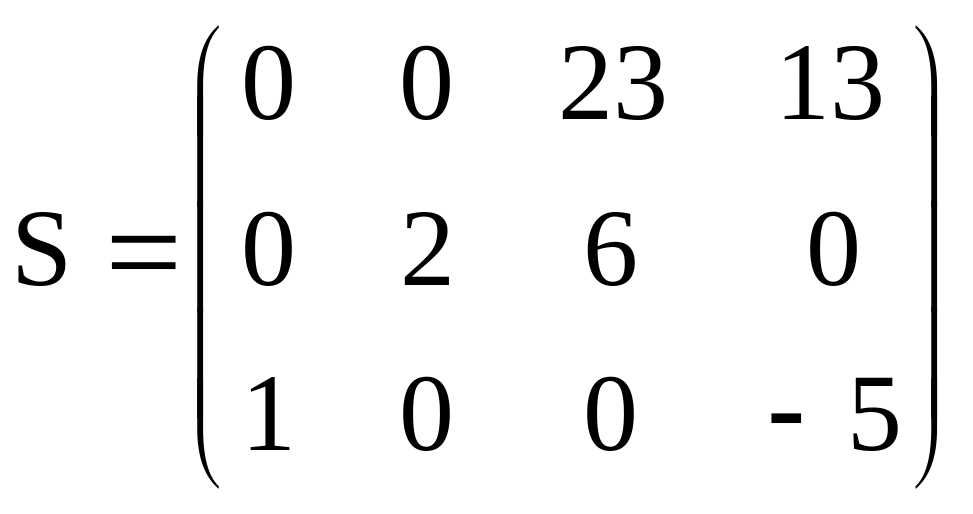
3 шаг. Построение цикла пересчета.

Среди отрицательных элементов матрицы оценок выбираем наименьшее. В нашем случае это –5, которое находится в клетке (3,4). Эта свободная клетка будет вершиной цикла пересчета. Строим цикл пересчета.

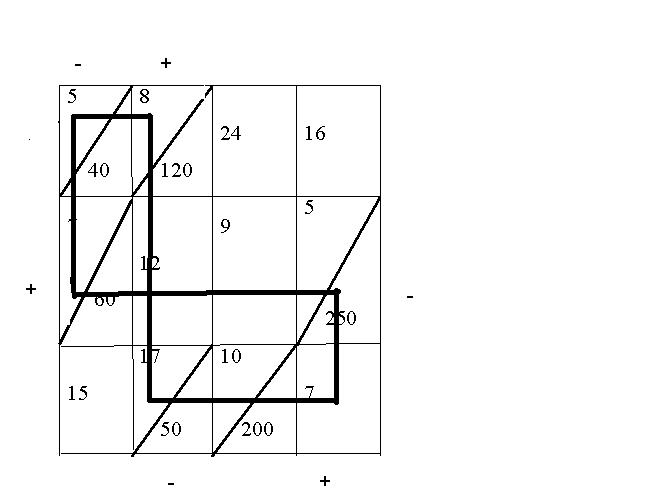
При построении цикла мы учли правило о том, что в одной строке (столбце) может быть только одно звено, соединяющее только две клетки. В третьей строке две заполненные клетки. Клетку (3,3) мы из цикла исключаем.

В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.

Из клеток со знаком «–» находим наименьшую поставку. У нас три клетки со знаком «–». Это клетки (1,1), (2,4) и (3,2). Наименьшая поставка находится в клетке (1,1) и она равна 40. Эту поставку передаем по циклу. В клетки с «+» ее прибавляем, с «–», соответственно, вычитаем.

Окончательно получаем новую распределительную таблицу:

	5	8 160	24	16
	7 100	12	9	5 210
	15	17 10	10 200	7 40

3 итерация.

1 шаг. Нахождение потенциалов строк и столбцов.

Находим потенциалы строк и столбцов.

2 шаг. Нахождение матрицы оценок.

Получаем матрицу оценок:

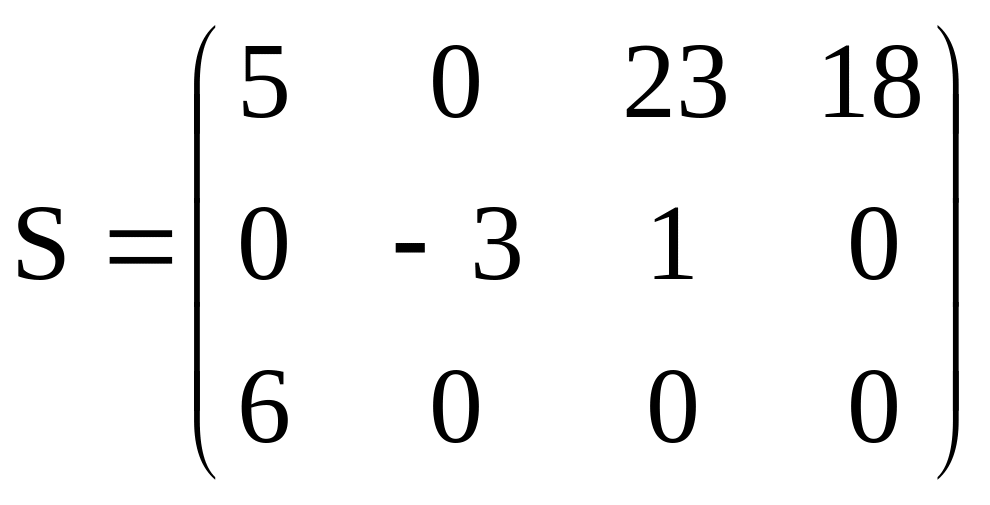
3 шаг. Построение цикла пересчета.

Среди отрицательных элементов матрицы оценок выбираем наименьшее. В нашем случае это –3, которое находится в клетке (2,2). Эта свободная клетка будет вершиной цикла пересчета. Строим цикл пересчета.

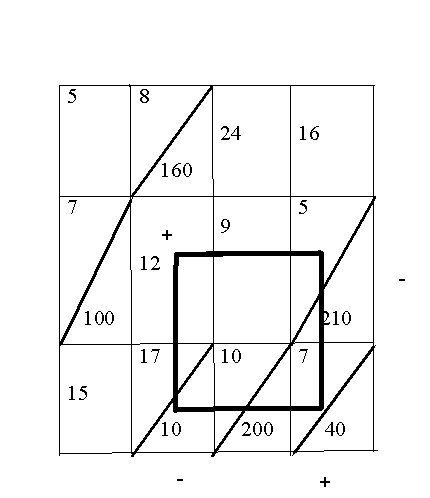
В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.

Из клеток со знаком «–» находим наименьшую поставку. У нас две клетки со знаком «–». Это клетки (2,4) и (3,2). Наименьшая поставка находится в клетке (3,2) и она равна 10. Эту поставку передаем по циклу. В клетки с «+» ее прибавляем, с «–», соответственно, вычитаем.

Окончательно получаем новую распределительную таблицу:

	5	8 160	24	16
	7 100	12 10	9	5 200
	15	17	10 200	7 50

4 итерация.

1 шаг. Нахождение потенциалов строк и столбцов.

Находим потенциалы строк и столбцов.

2 шаг. Нахождение матрицы оценок.

Получаем матрицу оценок:

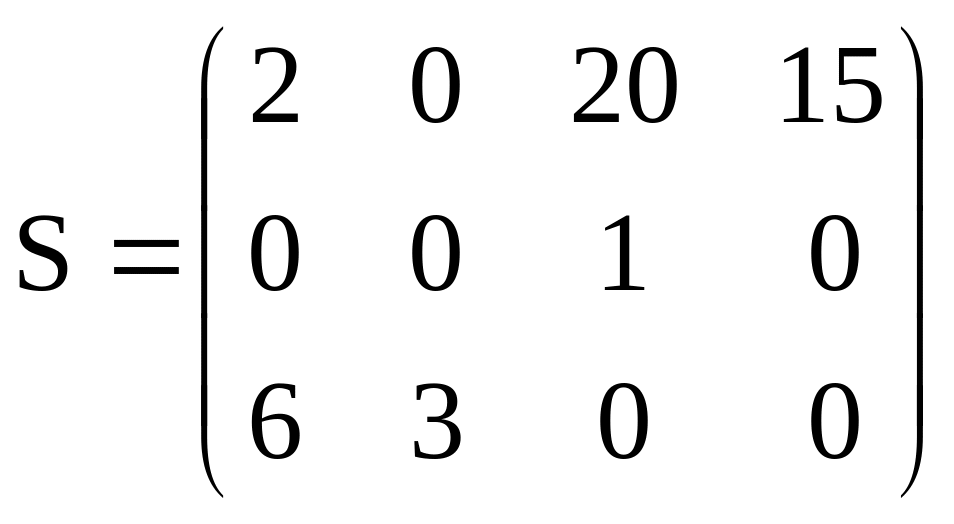
Получили, что все элементы матрицы оценок неотрицательные, следовательно получили оптимальное распределение поставок. Найдем наименьшие затраты на перевозку груза:

Напомним, что при первоначальном распределении поставок, найденном методом наименьших затрат, суммарные затраты составили 6040 у. е.

Ответ. Оптимальный план распределения:

5	8 160	24	16
7 100	12 10	9	5 200
15	17	10 200	7 50

Минимальные суммарные затраты составляют 5450 у.е.